Sieben-Parameter-Transformation

Die Helmert-Transformation (nach Friedrich Robert Helmert, 1843-1917; auch: 7-Parameter-Transformation) ist eine Koordinatentransformation für dreidimensionale kartesische Koordinaten, die in der Geodäsie häufig zur verzerrungsfreien Umrechnung von einem in ein anderes, ebenfalls dreidimensionales System genutzt wird:

X_T = C + μRX

• X_T ... transformierter Vektor
• X ... Ausgangsvektor

Die Parameter sind:

• C ... Verschiebungsvektor. Enthält die drei Verschiebungen entlang der Koordinatenachsen
• μ ... Maßstabsfaktor
• R ... Drehmatrix. Besteht aus drei Drehwinkeln (geringfügige Drehungen um die Koordinatenachsen) r_x, r_y, r_z. Die Drehmatrix ist eine Orthogonalmatrix

Damit ist die Helmert-Transformation eine Ähnlichkeitstransformation. Sie ist eine Spezialisierung der Galilei-Transformationen, zu denen unter anderem affine und projektive Transformationen gehören; letztere verzerren allerdings die Streckenlängen.

Berechnung der Parameter

Wenn die Transformationsparameter unbekannt sind, können sie über identische Punkte (also Punkte, deren Koordinaten vor und nach der Transformation bekannt sind) berechnet werden. Da insgesamt 7 Parameter (3 Verschiebungen, 1 Maßstab, 3 Verdrehungen) zu bestimmen sind, müssen zumindest 2 Punkte und von einem 3. Punkt eine Koordinate (z. B. die z-Koordinate) bekannt sein. Damit entsteht ein Gleichungssystem mit sieben Gleichungen und ebensovielen Unbekannten, das gelöst werden kann.

In der Praxis wird man bestrebt sein, mehr Punkte zu verwenden. Durch diese Überbestimmung erhält man erstens eine Kontrolle über die Richtigkeit der verwendeten Punkte und zweitens die Möglichkeit einer statistischen Beurteilung des Ergebnisses. Die Berechnung erfolgt in diesem Fall mit einer Ausgleichung nach der gaußschen Methode der kleinsten Quadrate.

Um numerisch günstige Werte für die Berechnung der Transformationsparameter zu erhalten, werden die Berechnungen mit Koordinatendifferenzen, bezogen auf den Schwerpunkt der gegebenen Punkte, durchgeführt.

Zweidimensionaler Fall

Ein Spezialfall ist die zweidimensionale Helmert-Transformation. Hier werden nur 4 Parameter benötigt (2 Verschiebungen, 1 Maßstab, 1 Verdrehung) und die Ermittlung derselben kann bereits mit zwei identischen Punkten erfolgen; wenn mehr Punkte gegeben sind, erfolgt wiederum eine Ausgleichung.

Anwendung

Die Helmerttransformation wird unter anderem in der Geodäsie angewendet, um Koordinaten der Punkte von einem Koordinatensystem in ein anderes zu transformieren. Damit ist z. B. die Umrechnung von Punkten der regionalen Landesvermessung in das für GPS-Ortungen benutzte WGS84 möglich.

Dabei werden die Gauß-Krüger-Koordinaten x,y plus der Höhe H schrittweise in 3D-Werte umgerechnet:

1. Berechnung der ellipsoidischen Breite, Länge und Höhe (B, L, H)
2. Berechnung von X, Y, Z bezüglich des Referenzellipsoides der Landesvermessung
3. 7-Parameter-Transformation (wodurch sich X, Y, Z fast gleichmäßig um maximal einige hundert Meter ändern und die Strecken um einige mm pro km).
4. Dadurch werden terrestrisch vermessene Positionen mit GPS-Daten vergleichbar; letztere können - in umgekehrter Reihenfolge transformiert - als neue Punkte in die Landesvermessung eingebracht werden.

Der 3. Schritt besteht in der Anwendung einer Drehmatrix, der Multiplikation mit einem Maßstabsfaktor μ = 1 + m (µ liegt nahe beim Wert 1) und der Addition einer Verschiebung C.

Da die Teiloperationen dieser Transformation allesamt nur kleine Änderungen bewirken, können die Koordinaten eines Referenzsystems B durch folgende Formel aus dem Referenzsystem A hergeleitet werden:

$\begin{bmatrix}X\\Y\\Z\end{bmatrix}^B=\begin{bmatrix}c_x\\c_y\\c_z\end{bmatrix}+\begin{bmatrix}1+m&-r_z&r_y\\r_z&1+m&-r_x\\-r_y&r_x&1+m\end{bmatrix}\cdot\begin{bmatrix}X\\Y\\Z\end{bmatrix}^A$

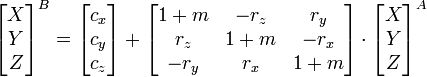
wobei die Drehwinkel r_x, r_y und r_z mit ihrem Wert im Bogenmaß einzusetzen sind.

Oder für jede einzelne Komponente:

$\begin{matrix} X_B=c_x+(1+m)\cdot X_A-r_z\cdot Y_A+r_y\cdot Z_A\\ Y_B=c_y+r_z\cdot X_A+(1+m)\cdot Y_A-r_x\cdot Z_A\\ Z_B=c_z-r_y\cdot X_A+r_x\cdot Y_A+(1+m)\cdot Z_A\\ \end{matrix}$

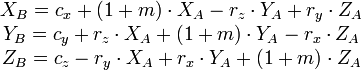
Für die Rücktransformation werden alle Parameter mit -1 multipliziert.

Die 7 Parameter werden für die jeweilige Region (Vermessungseparat, Bundesland etc.) mit 3 oder mehr "identischen Punkten" beider Systeme bestimmt. Bei Überbestimmung werden die kleinen Widersprüche (meist nur einige cm) durch Ausgleichung nach der Methode der kleinsten Quadrate ausgeglichen - das heißt, auf die statistisch plausibelste Weise beseitigt.

Standardparametersätze

Gebiet	Startsystem	Zielsystem	cx (Meter)	cy (Meter)	cz (Meter)	m (ppm)	rx (Bogensekunde)	ry (Bogensekunde)	rz (Bogensekunde)
England, Schottland, Wales	WGS84	OSGB36	-446,448	125,157	-542,06	20,4894	-0,1502	-0,247	-0,8421
Irland	WGS84	Ireland 1965	-482,53	130,596	-564,557	-8,15	1,042	0,214	0,631
Deutschland	WGS84	DHDN/Potsdam 2001	-598,1	-73,7	-418,2	-6,7	0,202	0,045	-2,455
Deutschland	WGS84	Pulkowo S42/83 2001	-24,9	126,4	93,2	-1,01	-0,063	-0,247	-0,041
Österreich (BEV)	WGS84	MGI	-577,326	-90,129	-463,919	-2,423	5,137	1,474	5,297
Schweiz	WGS84	LV95	-674.374	-15.056	-405.346	0	0	0	0
USA	WGS84	Clarke 1866	8	-160	-176	0	0	0	0

Bei den Beispielen handelt es sich um Standardparametersätze für die 7-Parameter-Transformation (oder: Datumstransformation) zwischen zwei Ellipsoiden. Für die Transformation in der Gegenrichtung muss bei allen Parametern das Vorzeichen geändert werden. Die Drehwinkel r_x, r_y und r_z werden manchmal auch als κ, φ und ω bezeichnet. Die Datumstransformation von WGS84 nach Bessel ist insofern interessant, als sich die GPS-Technologie auf den WGS84-Ellipsoiden bezieht, das in Deutschland verbreitete Gauß-Krüger-Koordinatensystem in der Regel jedoch auf den Ellipsoiden nach Bessel.

Da die Erde keine perfekte Ellipsoid-Form hat, sondern als Geoid beschrieben wird, genügt für eine Datumstransformation mit Vermessungsgenauigkeit der Standardparametersatz nicht. Die Geoidform der Erde wird stattdessen durch eine Vielzahl von Ellipsoiden beschrieben. Je nach tatsächlichem Standort werden die Parameter des "lokal bestangleichenden Ellipsoiden" verwendet. Diese Werte können stark von den Standardwerten abweichen, führen jedoch in der Transformationsrechnung in der Regel nur zu Änderungen des Ergebnisses im Zentimeterbereich.

Einschränkungen

Da sie nur einen Maßstabsfaktor kennt, kann die Helmert-Transformation als Ähnlichkeitstransformation nicht verwendet werden für:

• Die Entzerrung von Messbildern, Fotos, hier ist eine projektive Transformation zu verwenden.
• Die Ausgleichung eines Papierverzugs beim Scannen von alten Plänen und Karten. In diesen Fällen ist eine affine Transformation zu verwenden.

Siehe auch

Bezugssystem, Global Positioning System, Galileo, Ingenieurgeodäsie

Weblinks

• http://www.w-volk.de/museum/mathex02.htm
• http://www.geocities.com/mapref/savpub/savpub-23.htm#item40 (Geometrie beim Datenaustausch)
• http://www.mapref.org/