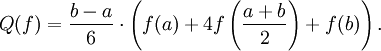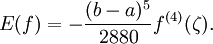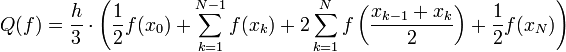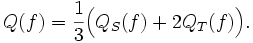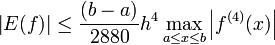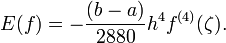Simpsonsche Regel

Simpsonsche Regel

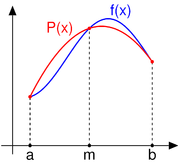
Die Simpsonregel (auch simpsonsche Formel) ist ein Verfahren der numerischen Quadratur, bei dem eine Näherung zum Integral einer Funktion f(x) im Intervall [a,b] berechnet wird, indem man die Kurve f(x) durch eine Parabel annähert. Die Formel wurde erstmals benutzt von Evangelista Torricelli, ist aber benannt nach dem englischen Mathematiker Thomas Simpson. Sie ist die allgemeine Formulierung der Keplerschen Fassregel, die Johannes Kepler schon 200 Jahre früher aufstellte.

Simpsonsche Formel

Die Parabel wird als Interpolationspolynom durch Funktionswerte an den Stellen 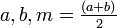a, b, m=\tfrac{(a+b)}2 gelegt. Das Integral nähert man dann durch das Integral der Parabel an.

Inhaltsverzeichnis

Die Formel

Mit der obigen Definition ergibt sich dann

Q(f) = \frac{b-a}{6} \cdot \left( f(a)+4f \left( \frac{a+b}{2} \right)+f(b) \right).

Darstellung als Runge-Kutta-Verfahren

Die Simpsonregel lässt sich auch als Runge-Kutta-Verfahren darstellen, und zwar mit dem Butcher-Schema

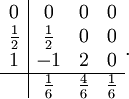
\begin{array}{c|ccc} 0 & 0 & 0 & 0\\ \frac{1}{2} & \frac{1}{2} & 0 & 0\\ 1 & -1 & 2 & 0\\ \hline & \frac{1}{6} & \frac{4}{6} & \frac{1}{6} \end{array}.

Restglied

Ist f(x) viermal stetig differenzierbar in [a,b], dann gilt für den Fehler E(f) die Abschätzung

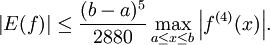
\left| E(f) \right| \le \frac{(b-a)^5}{2880} \max_{a\le x \le b} {\left| f^{(4)}(x) \right|}.

Ist f(x) zusätzlich noch reellwertig, dann gilt mit einer Zwischenstelle ζ aus [a,b] für das Restglied

E(f) = - \frac{(b-a)^5}{2880}{{f^{(4)}(\zeta)}}.

Diese Restglieddarstellung wurde 1887 von Giuseppe Peano gefunden.

Summierte simpsonsche Formel

Um das Integral noch besser annähern zu können unterteilt man das Intervall [a,b] in N nebeneinanderliegende, gleich große Teilintervalle der Länge h. In jedem Teilintervall wendet man die simpsonsche Formel für die einzelnen Teilflächen an und addiert danach die entstandenen Näherungen. Damit erhält man die summierte oder zusammengesetzte Simpsonregel

Q(f)=\frac h3 \cdot \left( \frac 12 f(x_0)+\sum_{k=1}^{N-1}f(x_k)+2\sum_{k=1}^{N}f \left( \frac{x_{k-1}+x_k}2 \right)+\frac 12 f(x_N) \right)
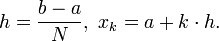
mit h = \frac{b-a}{N}, \ x_k=a+k\cdot h.

Man sieht leicht einen Zusammenhang mit der Sehnentrapezformel QS(f) und der Tangententrapezformel QT(f):

Q(f)=\frac 13 \Big( Q_S(f)+2Q_T(f) \Big).

Die Fehlerabschätzung für das Restglied lautet nun

\left| E(f) \right| \le \frac{(b-a)}{2880}h^4 \max_{a\le x \le b} {\left| f^{(4)}(x) \right|}

beziehungsweise für reellwertige Funktionen mit einer Zwischenstelle ζ aus dem Intervall [a,b]

E(f)=-\frac{(b-a)}{2880}h^4f^{(4)}(\zeta).

Wikimedia Foundation.

Игры ⚽ Поможем сделать НИР

Schlagen Sie auch in anderen Wörterbüchern nach:

  • Simpsonsche Regel — Simpsonsche Regel, eine von dem engl. Mathematiker Simpson herrührende Formel zur angenäherten Berechnung des Inhalts von ebenen Flächen und von Körpern. Ist z. B. der Flächenraum zu berechnen, der von der Geraden A0A2, von den darauf senkrechten …   Meyers Großes Konversations-Lexikon

  • simpsonsche Regel —   [ sɪmpsn ; nach T. Simpson], Näherungsformel zur Berechnung von Flächen, die sich als Integral f (x) dx darstellen lassen. Hierzu zerlegt man das Intervall [a, b] in n Teile (n gerade) durch die Punkte …   Universal-Lexikon

  • Simpsons Regel — Simpsons Regel, Näherungsformel zur Flächenberechnung (s.a. Bd. 4, S. 70). Die Auswertung des bestimmten Integrals kann annähernd nach der Formel: erfolgen, in welcher n eine beliebige ganze Zahl und der vorletzte Wert in den runden Klammern …   Lexikon der gesamten Technik

  • Simpson-Regel — Die Simpsonregel (auch simpsonsche Formel) ist ein Verfahren der numerischen Quadratur, bei dem eine Näherung zum Integral einer Funktion f(x) im Intervall [a,b] berechnet wird, indem man die Kurve f(x) durch eine Parabel annähert. Die Formel… …   Deutsch Wikipedia

  • Planimeter [1] — Planimeter (Flächenmesser), Instrumente zur graphischen oder mechanischen Bestimmung des Flächeninhalts von Figuren, welche in einer Ebene liegen oder auf eine solche abgewickelt werden können. Es handelt sich bei diesen Berechnungen zumeist um… …   Lexikon der gesamten Technik

  • Quadratur — (lat.), die Verwandlung einer von geraden und krummen Linien begrenzten Figur in ein Quadrat, das denselben Flächeninhalt hat, dann auch allgemeiner die Berechnung des Inhaltes einer solchen Figur, d. h. die Ermittelung der Zahl, die angibt, wie… …   Meyers Großes Konversations-Lexikon

  • Numerische Mathematik — Numerik * * * numerische Mathematik,   Numerik, Teilgebiet der Mathematik, in dem Methoden zur zahlenmäßigen (numerischen) Berechnung von Werten mathematischer Objekte untersucht werden. Dabei spielen besonders Näherungsverfahren (Approximation)… …   Universal-Lexikon

  • Simpson —   [ sɪmpsn],    1) George Gaylord, amerikanischer Paläontologe, * Chicago (Illinois) 16. 6. 1902, ✝ Tucson (Arizona) 6. 10. 1984; ab 1945 Professor an der Columbia University, ab 1959 an der Harvard University, ab 1967 an der University of… …   Universal-Lexikon

  • Bestimmtes Integral — Anschauliche Darstellung des Integrals als Flächeninhalt S unter einer Kurve der Funktion f im Integrationsbereich von a bis b. Die Integralrechnung ist neben der Differentialrechnung der wichtigste Zweig der mathematischen Disziplin der …   Deutsch Wikipedia

  • Dreifachintegral — Anschauliche Darstellung des Integrals als Flächeninhalt S unter einer Kurve der Funktion f im Integrationsbereich von a bis b. Die Integralrechnung ist neben der Differentialrechnung der wichtigste Zweig der mathematischen Disziplin der …   Deutsch Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”