Simuliertes Ausglühen

Die simulierte Abkühlung (Englisch simulated annealing) ist ein heuristisches Optimierungsverfahren des Operations Research. Das Verfahren wird zum Auffinden einer approximativen Lösung von Optimierungsproblemen eingesetzt, die durch ihre hohe Komplexität das vollständige Ausprobieren aller Möglichkeiten und einfache mathematische Verfahren ausschließen. Benutzt wird dieses Verfahren zum Beispiel beim Floorplanning im Laufe eines Chipentwurfs.

Grundidee ist die Nachbildung eines Abkühlungsprozesses, etwa beim Glühen in der Werkstoffkunde. Nach Erhitzen eines Metalls sorgt die langsame Abkühlung dafür, dass die Moleküle ausreichend Zeit haben, sich zu ordnen und stabile Kristalle zu bilden. Dadurch wird ein energiearmer Zustand, nahe am Optimum erreicht.

Übertragen auf das Optimierungsverfahren entspricht die Temperatur einer Wahrscheinlichkeit, mit der sich ein Zwischenergebnis der Optimierung auch verschlechtern darf. Der Metropolisalgorithmus ist die Grundlage der simulierten Abkühlung. Im Gegensatz zu einem Lokale-Suche-Algorithmus kann das Verfahren ein lokales Optimum wieder verlassen und ein besseres finden.

Algorithmus

Problemstellung

Gegeben sei der Wertebereich D, eine Fitness-Funktion 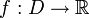$f : D \rightarrow \mathbb{R}$, ein Umgebungsbegriff U(x) und ein Abbruchkriterium

Gesucht ist eine approximative Lösung des globalen Minimums von f über D.

Initialisierung

Wähle eine Startlösung 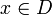$x \in D$. Wähle eine monoton gegen Null fallende Temperaturfolge 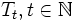$T_t, t \in \N$ und eine Folge 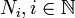$N_i, i \in \N$, die angibt, wieviele Schritte eine Temperatur T_t beibehalten wird. Startzeiten t = 0 und i = 1.

Lokale Veränderung

Falls 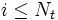$i \le N_t$: Wähle einen Nachbarn 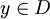$y \in D$ aus der Umgebung U(x), sonst setze i = 1 und t = t + 1 und suche wieder einen Nachbarn.

Selektion

• Gilt 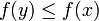$f(y) \le f(x)$, setze x = y und, falls 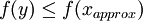$f(y) \le f(x_{approx})$, setze x_approx = y
• Gilt 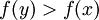$f(y) > f(x)\,$, setze x = y nur mit Wahrscheinlichkeit $\exp \left( -\frac{f \left( y \right) - f \left( x \right)}{T_t} \right)$.

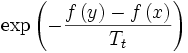Abbruch oder Weiter

Wurde das x nicht durch y ersetzt, setze i = i + 1 und beginne wieder mit einer lokalen Veränderung.

Sonst, falls die Abbruchbedingung zudem nicht erfüllt und damit die approximative Lösung x_approx gefunden ist, beginne im nächsten Zeittakt t = t + 1 wieder mit einer lokalen Veränderung und setze i = 1.

Erläuterungen

Die Wahrscheinlichkeit 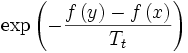$\exp \left( -\frac{f \left( y \right) - f \left( x \right)}{T_t} \right)$, dass ein schlechteres y akzeptiert wird, ist wegen 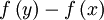$f \left( y \right) - f \left( x \right)$ für geringere Verschlechterungen größer und, weil T_t eine monoton fallende Folge ist, am Anfang des Verfahrens ebenfalls wahrscheinlicher.

Wie ein Nachbar gewählt werden sollte, hängt von dem vorliegenden Problem ab. In der Informatik ist häufig der Wertebereich D = {0,1}ⁿ und 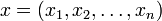$x = (x_1, x_2, \ldots, x_n)$ wird als Bit–Vektor betrachtet. Ein Nachbar y von x kann z.B. durch das flippen (invertieren) eines oder mehrerer Bits gewählt werden (siehe Wegener 2005).

Es sind verschiedene Abbruchbedingungen denkbar. Zum Beispiel wird nur eine maximale Anzahl von Durchläufen erlaubt, eine ausreichende Fitness definiert, eine Untergrenze für die Abkühlung festgelegt oder x hat sich über mehrere Zeitpunkte t nicht mehr geändert.

Graphische Verdeutlichung

Das Problem des simulierten Ausglühens kann man sich graphisch verdeutlichen. ^[1]

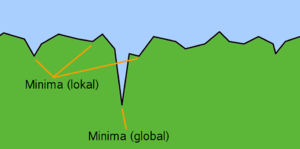
Angenommen, man sucht in einer zweidimensionalen Landschaft den (global) tiefsten Punkt. Die Landschaft selbst besteht aus vielen unterschiedlich tiefen Dellen. Die einfache Suchstrategie (suche den nächsten tiefsten Punkt) entspricht dem Verhalten einer Kugel, welche in dieser Landschaft ausgesetzt wird. Sie rollt zum nächsten lokalen Minimum und bleibt dort. Bei der simulierten Auskühlung wird der Kugel immer wieder ein Stoß versetzt. Dieser ist stark genug, um die Kugel aus einer flachen Delle (lokales Minimum) zu entfernen, reicht aber nicht aus, um aus dem globalen Minimum zu fliehen.

Diese Verbildlichung zeigt auch, dass das Verfahren unter bestimmten Bedingungen (und nur unter diesen) sicher das globale Minimum finden kann:

1. Das globale Minimum muss sich deutlich von den lokalen Minima unterscheiden.
2. Die zugeführte Energie muss geringer sein als zur Flucht aus dem globalen Minimum nötig, aber höher als nötig um aus den lokalen Minima zu fliehen.
3. Die Suche darf erst abgebrochen werden, wenn ein Minimum gefunden wurde, das nicht mehr verlassen werden kann.

Einzelnachweise

1. ↑ Google TechTalk Vortrag Eine kurze aber sehr verständliche Erklärung zum Thema findet man ab Minute 35.

Siehe auch

• Schwellenakzeptanz (threshold Accepting)
• Deterministic Annealing
• Sintflutalgorithmus
• Metropolisalgorithmus

Weblinks

• Interaktives Java-Applet zur Demonstration
• Java-Applet zum Vergleich von Simulated Annealing und Ameisenalgorithmen
• Interaktive Demonstration zum Ausprobieren

Literatur

• Ingo Wegener: Simulated Annealing Beats Metropolis in Combinatorial Optimization. In: Lecture Notes in Computer Science. 3580, Springer, Berlin/Heidelberg 2005, ISBN 978-3-540-27580-0, S. 589-601 (doi:10.1007/11523468) (Für ein einfach zu beschreibendes Problem wird gezeigt, dass unabhängig von der Temperatur die simulierte Abkühlung effizienter ist als der Metropolisalgorithmus.).