Situs (Mathematik)

Eine Grothendieck-Topologie ist ein mathematisches Konzept, das es erlaubt, in einem abstrakten kategoriellen Rahmen eine Garbentheorie und eine Kohomologietheorie zu entwickeln. Eine Kategorie, auf der eine Grothendieck-Topologie erklärt ist, nennt man einen Situs. Dieses Konzept wurde um 1960 von Alexander Grothendieck entwickelt, um in der algebraischen Geometrie in positiver Charakteristik einen Ersatz für die topologischen Kohomologietheorien wie bspw. die singuläre Kohomologie zu haben. Die Motivation hierfür kam von den Vermutungen von André Weil, die einen engen Zusammenhang zwischen der topologischen Gestalt (etwa den Bettizahlen) einer Varietät und der Anzahl der Punkte auf ihr über einem endlichen Körper voraussagte (Weil-Vermutungen). Die in diesem Kontext eingeführte étale Topologie zusammen mit der étalen Kohomologie und der l-adischen Kohomologie ermöglichte schließlich den Beweis der Weil-Vermutungen durch Pierre Deligne.

Formale Definition

Eine Grothendieck-Topologie in einer Kategorie C ist gegeben, indem man für jedes Objekt U aus C Familien von Morphismen 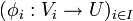$(\phi_i: V_i\to U)_{i\in I}$, als überdeckende Familien von U auszeichnet. Diese Familien müssen folgende Axiome erfüllen:

• Ein Isomorphismus 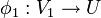$\phi_1: V_1\to U$ ist eine überdeckende Familie von U.

• Wenn 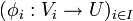$(\phi_i: V_i\to U)_{i\in I}$ eine überdeckende Familie von U ist und 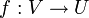$f: V\to U$ ein Morphismus, dann existiert der Pullback 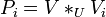$P_i = V\ast_U V_i$ für jedes i aus I und die induzierte Familie 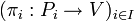$(\pi_i: P_i \to V)_{i\in I}$ ist eine überdeckende Familie für V.

• Wenn 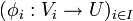$(\phi_i: V_i\to U)_{i\in I}$ eine überdeckende Familie von U ist und wenn für jedes i aus I, 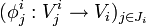$(\phi_j^i: V_j^i\to V_i)_{j\in J_i}$ eine überdeckende Familie von V_i ist, so ist $(\phi_i\phi_j^i: V_j^i\to U)_{i\in\ I, j\in J_i}$ eine überdeckende Familie von U.

Das einfachste Beispiel für eine Grothendieck-Topologie ist gegeben durch die Kategorie der offenen Mengen eines topologischen Raumes (mit den Inklusionen als Morphismen), wobei eine Familie 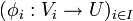$(\phi_i: V_i\to U)_{i\in I}$ eine überdeckende Familie ist, wenn die Vereinigung der V_i ganz U ist.

Garben

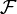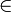Eine Prägarbe auf einer Kategorie C ist ein kontravarianter Funktor $\mathcal F$: C $\rightarrow$ A in eine Kategorie A, etwa die Kategorie der Mengen oder die Kategorie der abelschen Gruppen. Wenn C eine Grothendieck-Topologie besitzt, so nennt man eine Prägarbe eine Garbe, wenn für jede überdeckende Familie {φ_i: V_i $\rightarrow$ U}_i$\in$I die Sequenz :$\mathcal F(U)\rightarrow \prod\mathcal F(V_i)\,\begin{matrix}\rightarrow\\[-,7em]\rightarrow\end{matrix}\,\prod\mathcal F(V_i\cap V_j),$ exakt ist, d.h. 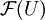wenn $\mathcal F(U)$ der Differenzkern der beiden rechten Pfeile ist.

Wie im Fall eines topologischen Raumes kann man Prägarben vergarben. Ebenso kann man verschiedene Kohomologietheorien entwickeln, etwa Cech-Kohomologie.

Die Gesamtheit aller Garben auf einem Situs nennt man Topos.