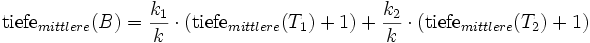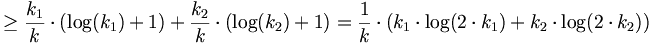Sortieralgorithmus

Ein Sortierverfahren ist ein Algorithmus, der dazu dient, eine Liste von Elementen zu sortieren. Voraussetzung ist, dass auf der Menge der Elemente eine strenge schwache Ordnung definiert ist, z. B. die lexikographische Ordnung von Zeichenketten oder die numerische Ordnung von Zahlen.

Es gibt verschiedene Sortierverfahren, die unterschiedlich effizient arbeiten. Die Komplexität eines Algorithmus, also die Anzahl der nötigen Operationen, wird üblicherweise in der Landau-Notation dargestellt. Einige Sortierverfahren benötigen außerdem neben dem zur Speicherung des Arrays nötigen noch weiteren Speicherplatz. Komplexität und Speicherbedarf hängen bei einigen Sortierverfahren von der anfänglichen Anordnung der Werte im Array ab, man unterscheidet dann zwischen Best Case (bester Fall), Average Case (Durchschnittsverhalten) und Worst Case (schlechtester Fall).

Man unterscheidet zudem zwischen stabilen und instabilen Sortierverfahren. Stabile Sortierverfahren sind solche, die die relative Reihenfolge von Elementen, die bezüglich der Ordnung äquivalent sind, nicht verändern, während instabile Sortierverfahren dies nicht garantieren.

Zudem unterscheidet man zwischen Sortierverfahren, die in-place (auch in situ) arbeiten, d. h. die mit einer von der Anzahl der zu sortierenden Elemente unabhängigen Menge zusätzlichen Speicherplatzes funktionieren, und solchen, die dies nicht tun (out-of-place oder ex situ genannt).

Und man unterscheidet auch zwischen natürlichen Sortierverfahren, die bei vorsortierten Daten schneller arbeiten als bei unsortierten Daten, und solchen, die es nicht tun. Algorithmen, bei denen der Kontrollfluss von den Daten abhängt, nennt man adaptiv und dementsprechend Sortierverfahren, die nicht von den Eingabedaten abhängen, nicht-adaptiv. Nicht-adaptive Algorithmen sind demnach besonders interessant für Hardware-Implementierungen.

Vergleichsbasiertes Sortieren

Allgemeine Verfahren basieren auf dem paarweisen Vergleich der zu sortierenden Elemente. Bei der Komplexitätsanalyse wird davon ausgegangen, dass der Aufwand zum Vergleich zweier Elemente konstant ist.

Sortierverfahren	Best-Case	Average-Case	Worst-Case	Stabil	Rekursiv	Zusätzlicher Speicherbedarf (sofern nicht in-place)
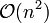
Binary Tree Sort	$\mathcal{O}( n \cdot \log (n) )$	$\mathcal{O}( n \cdot \log (n) )$	$\mathcal{O}(n^2)$	nein	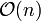	$\mathcal{O}( n )$
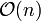
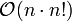
Bogosort	$\mathcal{O}( n )$	$\mathcal{O}( n \cdot n! )$	$\infty$	nein	-	-
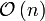
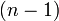
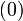
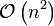
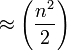
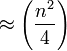
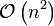
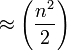
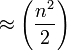
Bubblesort (Vergleiche) (Kopieraktionen)	$\mathcal{O}\left( n \right)$ $\left( n-1 \right)$ $\left( 0 \right)$	$\mathcal{O}\left( n^2 \right)$ $\approx \left( \frac{n^2}{2} \right)$ $\approx \left( \frac{n^2}{4} \right)$	$\mathcal{O}\left( n^2 \right)$ $\approx \left( \frac{n^2}{2} \right)$ $\approx \left( \frac{n^2}{2} \right)$	ja	nein	-
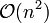
Combsort	$\mathcal{O}( n \cdot \log (n) )$	$\mathcal{O}( n \cdot \log (n) )$	$\mathcal{O}( n^2 )$	nein	nein	-
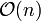
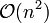
Gnomesort	$\mathcal{O}( n )$		$\mathcal{O}( n^2 )$	ja	nein	-
Heapsort	$\mathcal{O}( n \cdot \log (n) )$	$\mathcal{O}( n \cdot \log (n) )$	$\mathcal{O}( n \cdot \log (n) )$	nein	nein	-
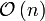
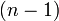
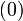
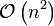
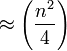
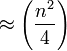
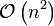
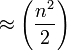
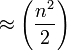
Insertionsort (Vergleiche) (Kopieraktionen)	$\mathcal{O}\left( n \right)$ $\left( n-1 \right)$ $\left( 0 \right)$	$\mathcal{O}\left( n^2 \right)$ $\approx \left( \frac{n^2}{4} \right)$ $\approx \left( \frac{n^2}{4} \right)$	$\mathcal{O}\left( n^2 \right)$ $\approx \left( \frac{n^2}{2} \right)$ $\approx \left( \frac{n^2}{2} \right)$	ja	nein	-
Introsort	$\mathcal{O}( n \cdot \log (n) )$	$\mathcal{O}( n \cdot \log (n) )$	$\mathcal{O}( n \cdot \log (n) )$	nein	ja	-
Merge Insertion	$\mathcal{O}( n \cdot \log (n) )$	$\mathcal{O}( n \cdot \log (n) )$	$\mathcal{O}( n \cdot \log (n) )$	ja	ja	implementierungsabhängig keine, 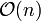$\mathcal{O}( n )$ oder $\mathcal{O}( n \cdot \log (n) )$
Mergesort	$\mathcal{O}( n \cdot \log (n) )$	$\mathcal{O}( n \cdot \log (n) )$	$\mathcal{O}( n \cdot \log (n) )$	ja	ja	bei Arrays: 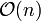$\mathcal{O}( n )$, je nach Implementierung auch $\mathcal{O}( n \cdot \log (n) )$
Natural Mergesort	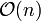$\mathcal{O}( n )$	$\mathcal{O}( n \cdot \log (n) )$	$\mathcal{O}( n \cdot \log (n) )$	ja	ja	bei Arrays: 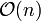$\mathcal{O}( n )$, je nach Implementierung auch $\mathcal{O}( n \cdot \log (n) )$
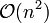
Quicksort	$\mathcal{O}( n \cdot \log (n) )$	$\mathcal{O}( n \cdot \log (n) )$	$\mathcal{O}( n^2 )$	nein	ja	-
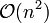
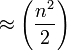
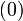
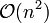
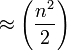
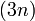
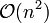
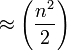
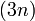
Selectionsort (Vergleiche) (Kopieraktionen)	$\mathcal{O}( n^2 )$ $\approx \left( \frac{n^2}{2} \right)$ $\left( 0 \right)$	$\mathcal{O}( n^2 )$ $\approx \left( \frac{n^2}{2} \right)$ $\left( 3n \right)$	$\mathcal{O}( n^2 )$ $\approx \left( \frac{n^2}{2} \right)$ $\left( 3n \right)$	nein	nein	-
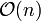
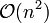
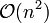
Shakersort (Cocktailsort)	$\mathcal{O}( n )$	$\mathcal{O}( n^2 )$	$\mathcal{O}( n^2 )$	ja		-
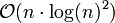
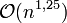
Shellsort		$\mathcal{O}( n \cdot \log (n)^2 )$	$\mathcal{O}( n^{1,25} )$	nein	nein	-
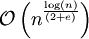
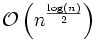
Slowsort	$\mathcal{O}\left(n^{\frac{\log(n)}{(2+e)}}\right)$	$\mathcal{O}\left( n^{\frac{\log(n)}{2}} \right)$		ja	ja	-
Smoothsort	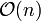$\mathcal{O}( n )$	$\mathcal{O}( n \cdot \log (n) )$	$\mathcal{O}( n \cdot \log (n) )$	nein		-
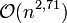
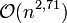
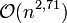
Stoogesort	$\mathcal{O}( n^{2,71} )$	$\mathcal{O}( n^{2,71} )$	$\mathcal{O}( n^{2,71} )$	nein	ja	-
Swap-Sort	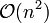		$\mathcal{O}( n^2 )$

Bei diesen Verfahren gilt das 0-1-Sortier-Lemma von Knuth: Wenn ein Sortieralgorithmus ausschließlich aus Operationen der Art „Vergleich-und-Austausch-wenn-größer“ besteht und wenn von vornherein (unabhängig von den zu sortierenden Daten) feststeht, an welchen Positionen die Werte miteinander verglichen und gegebenenfalls vertauscht werden, dann gilt: Der Algorithmus sortiert genau alle Eingabedatensätze, wenn er alle Eingabedatensätze sortiert, die nur aus Nullen und Einsen bestehen. Dieses Lemma sichert zu, dass bei bestimmten Sortieralgorithmen für den Nachweis der Korrektheit die Betrachtung von 0-1-Eingaben genügt.

Beweis der unteren Schranke für vergleichsbasiertes Sortieren

Es lässt sich beweisen, dass ein vergleichsbasiertes Sortierverfahren nicht schneller als 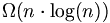$\Omega(n\cdot \log(n))$ sein kann:

Sei B der Entscheidungsbaum für die Zahlenfolge X (x1,....,xn). Da alle Permutationen von X das Ergebnis des Sortieralgorithmus sein könnten, muss der Entscheidungsbaum B mindestens n! Blätter haben. Da eine Mindestanzahl von Schritten gesucht ist, treten im Entscheidungsbaum keine unnötigen Vergleiche auf.

In einem Entscheidungsbaum mit n! Blättern beträgt die maximale und die mittlere Tiefe eines Blattes mindestens log(n!). Da eine untere Schranke gesucht ist, kann n! mittels 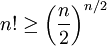$n! \ge \left( \frac{n}{2} \right)^{n/2}$ nach unten hin abgeschätzt werden. Damit gilt $\log(n!) \ge \left( \frac{n}{2} \right)\cdot\log\left( \frac{n}{2} \right)=\Omega(n\cdot\log(n))$.

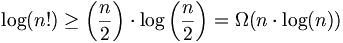Es bleibt noch zu zeigen, dass in einem Binärbaum mit k Blättern die maximale und die mittlere Tiefe eines Blattes mindestens log(k) beträgt. Angenommen B sei ein Binärbaum für welchen die obige Aussage nicht gilt. Seien T1 und T2 Teilbäume eines Binärbaumes mit k>2 Blättern. Für die Anzahl der Blätter k1 in T1 bzw. k2 in T2 gilt nun offensichtlich k1 < k, k2 < k und k1+k2 =k. Für die Tiefe jedes Blattes, bezogen auf die Wurzel von B, gilt: ...

$\mbox{tiefe}_{mittlere}(B)=\frac{k_1}{k}\cdot(\mbox{tiefe}_{mittlere}(T_1)+1)+\frac{k_2}{k}\cdot(\mbox{tiefe}_{mittlere}(T_2)+1)$

$\ge \frac{k_1}{k}\cdot(\log(k_1)+1)+\frac{k_2}{k}\cdot(\log(k_2)+1) = \frac{1}{k}\cdot(k_1\cdot\log(2\cdot k_1)+k_2\cdot \log(2\cdot k_2))$

Das Minimum dieser Funktion liegt nun bei k1 + k2 = k und k1 = k2 = k/2. Eingesetzt in obige Formel ergibt das:

$\mbox{tiefe}_{mittlere}(B) \ge \frac{1}{k}\cdot(\frac{k}{2}\cdot\log(k)+\frac{k}{2}\cdot\log(k))=\log(k)$.

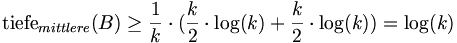Dies ergibt einen Widerspruch zur Annahme, womit obige Aussage bewiesen ist.

Nicht-vergleichsbasiertes Sortieren

Trotz des oben angegebenen Beweises ist es möglich, bestimmte Daten in linearer Zeit zu sortieren, allerdings nicht vergleichsbasiert. Dazu muss es sich um Daten handeln, bei denen sich aus dem Schlüssel eines Elementes auch ohne Vergleich mit den Schlüsseln anderer Elemente Information über die Position des Elementes in der sortierten Folge gewinnen lassen. In diesem Fall kann ein spezialisiertes Verfahren schneller sein.

Sortierverfahren	Zeit	Stabil	Rekursiv	Zusätzlicher Speicherbedarf
Bucketsort	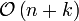$\mathcal{O}\left( n + k\right)$	ja	nein	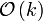$\mathcal{O}\left( k \right)$
Countingsort	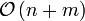$\mathcal{O}\left( n + m\right)$	ja	nein	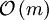$\mathcal{O}\left( m \right)$
Radixsort	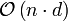$\mathcal{O}\left( n \cdot d\right)$	ja	möglich	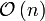$\mathcal{O}\left( n \right)$

Dabei stellt n die Anzahl der Elemente dar, k die Anzahl der möglichen Werte, m die Differenz aus Maximal- und Minimalwert der Eingabe und d die Anzahl der Stellen der längsten Eingabe.

Sortierung nach Beziehungen

Wenn nicht mehr nach Eigenschaften, sondern nur noch nach paarweisen Beziehungen sortiert werden kann, so spricht man von einer topologischen Sortierung. Dies ist beispielsweise der Fall, wenn Aufgaben erledigt werden müssen, manche Aufgaben aber unbedingt vor anderen durchzuführen sind, bei anderen jedoch die Reihenfolge keine Rolle spielt.

Für das topologische Sortieren gibt es Algorithmen, deren Laufzeit von der Anzahl der Beziehungen 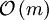$\mathcal{O}\left( m \right)$ abhängt. Topologisches Sortieren ist nicht möglich, wenn gegenseitige (zyklische) Abhängigkeiten bestehen. Eine topologische Sortierung muss nicht eindeutig sein.

Wenn die Beziehungen vollständig sind, also für je zwei Objekte eine Abhängigkeit vorgegeben ist, so geht die topologische Sortierung in eine gewöhnliche Sortierung über. Das Laufzeitverhalten der Algorithmen bei n Objekten ist dann $\mathcal{O}\left( 1 \right)$.

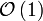Indirektes Sortieren

In den Fällen, bei denen das Umstellen der Daten mit hohem Aufwand verbunden ist, kann man auch indirektes Sortieren anwenden. Man benötigt dazu zusätzlichen Speicher proportional zur Anzahl der Elemente (in der Regel 4 Bytes pro Element). Dann wird dieses Array indirekt sortiert. Um die eigentlichen Daten letztendlich in die richtige Reihenfolge zu bringen ist ein zusätzlicher Aufwand von 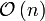$\mathcal{O}\left( n \right)$ erforderlich.

Literatur

• Donald E. Knuth: Sorting and Searching. Band 3 der Reihe The Art of Computer Programming. Addison Wesley, ISBN 0-201-89685-0
• Niklaus Wirth: Algorithmen und Datenstrukturen. Teubner Verlag, ISBN 3519222507
• Robert Sedgewick: Algorithms in Java, Part 1–4 Addison-Wesley, ISBN 0201361205
• Thomas H. Cormen, Charles Leiserson, Ronald L. Rivest, Clifford Stein: Introduction to Algorithms The MIT Press, ISBN 0-262-03293-7
• Thomas Ottmann, Peter Widmayer: Algorithmen und Datenstrukturen Spektrum Verlag, ISBN 3-8274-0110-0
• Anany Levitin: Introduction to The Design and Analysis of Algorithms Pearson Addison Wesley, ISBN 0-321-36413-9

Weblinks

• Visualisierung von Sortieralgorithmen mit Processing - Chronologische Visualisierungen von zwölf verschiedenen Sortieralgorithmen
• Grafischer Vergleich einiger Sortieralgorithmen (Java)
• VisuSort Framework – Visualisierung diverser Sortieralgorithmen (Windows)
• Übersicht und Beschreibung vielfältiger Sortieralgorithmen
• AniSort – Visualisierung von 6 verschiedenen Sortieralgorithmen (Java Applet)
• JavaScript – Interaktive Visualisierung verschiedener Sortieralgorithmen