- Span (Mathematik)
-
In der linearen Algebra ist die lineare Hülle einer Teilmenge A (eines K-Vektorraums V) die Menge aller Linearkombinationen mit Vektoren aus A und Skalaren des Körpers K. Die lineare Hülle bildet einen Untervektorraum. Dieser ist gleichzeitig der kleinste Untervektorraum, der A enthält.
Als Symbole für die lineare Hülle von A werden
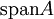 ,
, 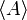 , L(S),
, L(S), 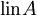 oder
oder 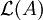 verwendet. Ist A endlich, etwa
verwendet. Ist A endlich, etwa 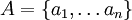 , werden doppelte Klammern vermieden indem die Schreibweisen
, werden doppelte Klammern vermieden indem die Schreibweisen 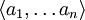 ,
, 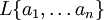 oder
oder 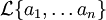 verwendet werden.
verwendet werden.Inhaltsverzeichnis
Definition
Konstruktive Definition
Ist V ein Vektorraum über einem Körper K und
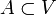 eine Teilmenge des Vektorraums, dann ist
eine Teilmenge des Vektorraums, dann istdie lineare Hülle von A. Die lineare Hülle ist die Menge aller endlichen Linearkombinationen der ai.
Im Fall einer endlichen Teilmenge A vereinfacht sich diese Definition zu
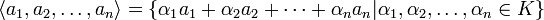 .
.
Die lineare Hülle der leeren Menge ist der Nullraum:
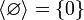 .
.
Andere Definitionen
Äquivalent (gleichwertig) zu der konstruktiven Definition sind die folgenden Definitionen:
- Die lineare Hülle einer Teilmenge A eines Vektorraums ist der kleinste lineare Unterraum, der die Menge A enthält.
- Die lineare Hülle einer Teilmenge A eines Vektorraums V ist die Schnittmenge aller linearen Unterräume U von V, die A enthalten.
Eigenschaften
- Die lineare Hülle einer Teilmenge eines Vektorraums V ist ein Unterraum von V.
- Für jeden Unterraum U eines Vektorraums V gilt
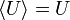 .
. - Eine Menge von Vektoren ist ein Erzeugendensystem ihrer linearen Hülle. Ist umgekehrt eine Menge von Vektoren ein Erzeugendensystem eines Unterraumes, so ist dieser ihre lineare Hülle.
- In der Menge T der Unterräume eines Vektorraumes (einschließlich des Gesamtraums) kann man die Operation „bilde die lineare Hülle der Vereinigungsmenge“ als zweistellige Verknüpfung einführen. Die dazu duale Verknüpfung ist dann die Schnittmengenbildung. Mit diesen Verknüpfungen bildet T dann einen Verband.
Beispiele
- Die beiden Vektoren (3,0,0) und (0,2,0) sind Elemente des reellen Vektorraums
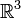 . Ihre lineare Hülle
. Ihre lineare Hülle 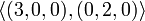 ist die x-y-Ebene.
ist die x-y-Ebene. - Sei
![K[[X]] = \left\lbrace \sum_{k=0}^{\infty} \alpha_k x^k | \alpha_k \in K \right\rbrace](/pictures/dewiki/101/ea362151f6d70bf27fe5e45164d8b35d.png) der Vektorraum der formalen Potenzreihen zum Körper K und
der Vektorraum der formalen Potenzreihen zum Körper K und 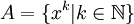 die Menge der Monome. Dann ist die lineare Hülle von A der Unterraum der Polynome.
die Menge der Monome. Dann ist die lineare Hülle von A der Unterraum der Polynome.
Literatur
- Siegfried Bosch: Lineare Algebra. Springer, 2001, ISBN 3-540-41853-9, S. 29–30
Wikimedia Foundation.

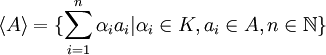
![\langle A \rangle = \{ \sum_{i=0}^n \alpha_i x^i | \alpha_i \in K, n \in \N \} = K[X]](/pictures/dewiki/55/7962cb5b30c415190d5343d68d0120cc.png)