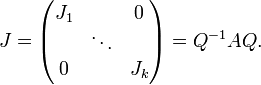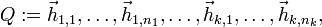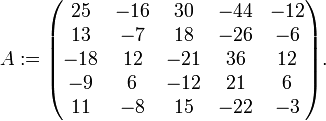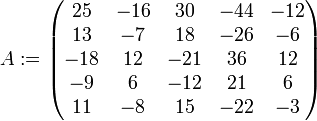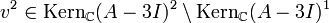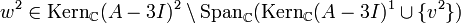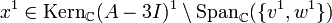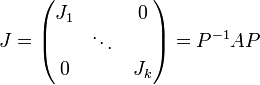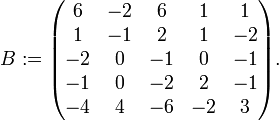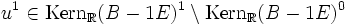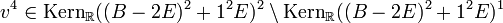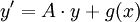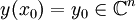- Jordanform
-
Die jordansche Normalform ist ein Begriff aus dem mathematischen Teilgebiet der linearen Algebra. Sie ist ein einfacher Vertreter der Äquivalenzklasse der zu einer trigonalisierbaren Matrix (trigonalisierbaren linearen Abbildung) ähnlichen Matrizen (linearen Abbildungen). Die Trigonalisierbarkeit ist gleichbedeutend damit, dass das charakteristische Polynom der Matrix (linearen Abbildung) vollständig in Linearfaktoren zerfällt. Benannt wurde die jordansche Normalform nach Marie Ennemond Camille Jordan, der sie 1871 im Zusammenhang mit der Lösung komplexer Differentialgleichungssysteme für komplexe Matrizen herleitete.
Die jordansche Normalform zu einer quadratischen Matrix A ist eine Matrix J in der folgenden Blockdiagonalform
Die Matrix Q ist die Matrix der Eigenvektoren und Hauptvektoren, aus denen sie spaltenweise besteht. Q − 1 bezeichnet dabei die inverse Matrix von Q. Die Ji sind die Jordan-Blöcke. Diese haben folgende Form:
Die λi sind dabei die Eigenwerte von A. Zu jedem Eigenwert λi gibt es seiner geometrischen Vielfachheit entsprechend viele Jordan-Blöcke. (Die geometrische Vielfachheit ist dabei die Dimension des Eigenraums zum Eigenwert λi.) Die Gesamtdimension aller Jordan-Blöcke eines Eigenwertes entspricht seiner algebraischen Vielfachheit, d. h. seiner Vielfachheit im charakteristischen Polynom.
In einem Jordanblock sind die sogenannten Jordanketten „gespeichert“ (siehe Hauptvektor). Besteht A z. B. nur aus einem Jordanblock mit Eigenwert λ und bezeichne vj den j-ten Hauptvektor (dabei ist v1 der Eigenvektor zum Eigenwert λ), dann gilt (A − λE)v1 = 0 und (A − λE)vj + 1 = vj für
 .
.Es existiert noch die alternative Darstellung der Jordanblöcke mit 1 in der unteren Nebendiagonalen.
Im Spezialfall einer diagonalisierbaren Matrix ist die jordansche Normalform eine Diagonalmatrix.
Zur Form von Q
Es seien
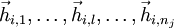 die Hauptvektoren der jeweils l-ten Stufe, wobei nj die Dimension des j-ten Jordankästchens ist.
die Hauptvektoren der jeweils l-ten Stufe, wobei nj die Dimension des j-ten Jordankästchens ist.Dann ist Q, definiert durch
eine Transformationmatrix, welche die Jordan-Normalform von A herstellt, wobei k die Anzahl der Jordankästchen war.
In Worten: Die Spalten von Q sind die Eigenvektoren mit den dazugehörigen Hauptvektoren in der Reihenfolge der dazugehörigen Jordankästchen. Allerdings ist Q nicht eindeutig bestimmt.
Algorithmus zur Bestimmung einer komplexen jordanschen Normalform
Für die jordansche Normalform eines Endomorphismus
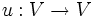 eines n-dimensionalen
eines n-dimensionalen  -Vektorraums V wählt man eine Basis
-Vektorraums V wählt man eine Basis 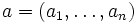 des Vektorraums V und berechnet die jordansche Normalform der Matrix von u in Bezug auf die Basis a, i. e. die Matrix zum Basiswechsel Ma(u).
des Vektorraums V und berechnet die jordansche Normalform der Matrix von u in Bezug auf die Basis a, i. e. die Matrix zum Basiswechsel Ma(u).Im Folgenden wird die komplexe jordansche Normalform einer (quadratischen) Matrix bestimmt.
Sei im Folgenden
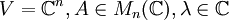 und En die Einheitsmatrix.
und En die Einheitsmatrix.Bestimmung der Eigenwerte
Mit Hilfe des charakteristischen Polynoms
- χA = det(λEn − A)
errechnet man aus seinen Nullstellen die (paarweise verschiedenen) Eigenwerte
Die Eigenwerte werden hier also nicht ihrer Vielfachheit entsprechend aufgeführt.
Bestimmung der Größe der Jordanblöcke
Hierfür muss man die Dimension der Potenzen der Eigenräume bestimmen. Das heißt, man berechnet
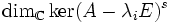 für
für 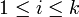 und
und 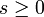 .
.Die Dimension des Kerns erhält man wiederum aus dem Dimensionssatz:
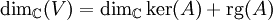 . Der Rang von A kann z. B. mit dem gaußschen Algorithmus bestimmt werden. Die Dimension wird ab einem bestimmten Wert für s (spätestens bei der Vielfachheit des Eigenwertes im charakteristischen Polynom) stationär.
. Der Rang von A kann z. B. mit dem gaußschen Algorithmus bestimmt werden. Die Dimension wird ab einem bestimmten Wert für s (spätestens bei der Vielfachheit des Eigenwertes im charakteristischen Polynom) stationär.Mit
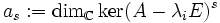 definiert man also positive Zahlen, um mit der Formel 2as − as − 1 − as + 1 die Anzahl der Jordankästchen der Größe s zum Eigenwert λi zu erhalten.
definiert man also positive Zahlen, um mit der Formel 2as − as − 1 − as + 1 die Anzahl der Jordankästchen der Größe s zum Eigenwert λi zu erhalten.Komplexe jordansche Normalform
Die erhaltenen Jordanblöcke schreibt man in eine Matrix und erhält die komplexe jordansche Normalform einer Matrix. Haben die Kästchen allesamt die Größe 1, liegt der Spezialfall einer Diagonalmatrix vor, und A ist somit diagonalisierbar.
Das Minimalpolynom
![g\in \mathbb C[X]](/pictures/dewiki/50/266296ec663b97518c799e12b5024b7b.png) von A erhält man aus
von A erhält man aus 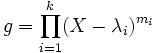 , worin mi die Größe des größten Jordanblocks zum Eigenwert λi bezeichnet.
, worin mi die Größe des größten Jordanblocks zum Eigenwert λi bezeichnet.Die jordansche Normalform ist bis auf die Reihenfolge der Kästchen eindeutig bestimmt. Sofern alle Eigenwerte in
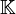 liegen, sind zwei Matrizen, welche dieselbe jordansche Normalform haben, zueinander ähnlich.
liegen, sind zwei Matrizen, welche dieselbe jordansche Normalform haben, zueinander ähnlich.Beispiel
Man betrachte die Matrix
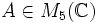 , die wie folgt definiert ist
, die wie folgt definiert istIhr charakteristisches Polynom lautet χ(A) = (X − 3)5. Somit besitzt diese Matrix genau einen Eigenwert, nämlich 3. Nun berechnen wir die as für
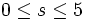 .
.rg(A − 3E5)0 ist die Einheitsmatrix, und diese hat vollen Rang, also 5. Die Dimension des Vektorraumes
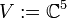 beträgt ebenso 5. Also ist
beträgt ebenso 5. Also ist 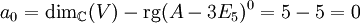 .
.- rg(A − 3E5)1 = 2. Somit ist
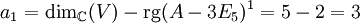 .
.
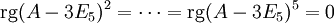 . Damit ist
. Damit ist 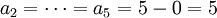 .
.
Die Anzahl der Jordankästchen mit Größe 1 sind 2a1 − a0 − a2 = 6 − 0 − 5 = 1 Stück.
Die Anzahl der Jordanblöcke mit Größe 2 sind 2a2 − a1 − a3 = 10 − 3 − 5 = 2 Stück.
Den anderen Kästchen bleibt jetzt nichts mehr anderes übrig, als die Größe 0 zu haben.
Somit ist
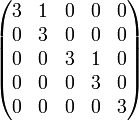 die jordansche Normalform von A. Das Minimalpolynom von A ist (X − 3)2.
die jordansche Normalform von A. Das Minimalpolynom von A ist (X − 3)2.Bestimmung einer Basistransformation zur komplexen jordanschen Normalform
Nun soll eine Basistransformationsmatrix
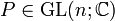 bestimmt werden, die
bestimmt werden, die- J = P − 1AP
erfüllt. Sie ist durch diese Gleichung bekanntlich nicht eindeutig bestimmt. Die Verfahren verwenden die vorherige Kenntnis der komplexen jordanschen Normalform J.
Ein ineffizienter Brute-Force-Ansatz
Ein erster, aber nicht sehr geschickter Ansatz wäre der folgende: J = P − 1AP ist offenbar äquivalent zu PJ − AP = 0. Durch komponentenweise Betrachtung erhält man daraus
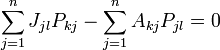 für alle
für alle 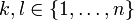 .
.
Dies ist ein lineares (homogenes) Gleichungssystem von n2 Gleichungen in den n2 Unbekannten
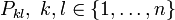 . Der Lösungsraum ist nichttrivial. Findet man unter den Lösungen
. Der Lösungsraum ist nichttrivial. Findet man unter den Lösungen 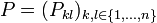 eine reguläre Matrix (so eine existiert auch, falls J die jordansche Normalform ist), so ist P eine Basistransformation mit J = P − 1AP.
eine reguläre Matrix (so eine existiert auch, falls J die jordansche Normalform ist), so ist P eine Basistransformation mit J = P − 1AP.Abgesehen davon, dass man noch durch geschickte Linearkombination der Basisvektoren des Lösungsraumes eine reguläre Matrix erzeugen muss (und zwar durch Ausprobieren, das ist eine ernstzunehmende algorithmische Schwachstelle), ist dieser Ansatz sehr ineffizient, da man ein unnötig großes Gleichungssystem lösen muss. Die Ursache besteht unter anderem darin, dass dieser Algorithmus keinen Gebrauch macht von den Informationen, die zur vorherigen Bestimmung der jordanschen Normalform ausgerechnet wurden. Er erkennt selbst im Fall einer diagonalisierbaren Matrix nicht, dass die Transformationsmatrix direkt durch die Eigenvektoren gegeben ist. Bereits bei kleinen Dimensionen wäre daher schon ein unverhältnismäßig großer Rechenaufwand nötig.
Ein Standard-Verfahren
Ein gängiges Verfahren, um eine Basistransformation zu erhalten, ist das folgende: Man bestimme (wie auch bei obigem naiven Ansatz) zunächst die Jordannormalform J. Dann hat man insbesondere schon alle Eigenwerte λ berechnet sowie die Kerne
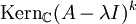 für alle
für alle 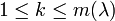 , worin
, worin 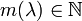 die Dimension des größten Jordanblocks zum Eigenwert λ bezeichnet. Anschließend arbeite man zur Bestimmung einer regulären Matrix P mit J = P − 1AP die Blöcke nacheinander ab. Dabei ist zu beachten, dass man bei Jordanblöcken zum selben Eigenwert stets vom größten Block zum kleinsten Block vorgeht.
die Dimension des größten Jordanblocks zum Eigenwert λ bezeichnet. Anschließend arbeite man zur Bestimmung einer regulären Matrix P mit J = P − 1AP die Blöcke nacheinander ab. Dabei ist zu beachten, dass man bei Jordanblöcken zum selben Eigenwert stets vom größten Block zum kleinsten Block vorgeht.Zu jedem Block der Größe k und Eigenwert λ werden k Spalten der Basistransformationsmatrix
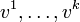 nach einem bestimmten Schema bestimmt. Wenn der Block in J die Spalten
nach einem bestimmten Schema bestimmt. Wenn der Block in J die Spalten 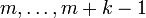 belegt, so werden die Vektoren
belegt, so werden die Vektoren 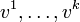 in P ebenso (von links nach rechts) in die Spalten
in P ebenso (von links nach rechts) in die Spalten 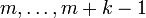 eingefügt. Die Vektoren
eingefügt. Die Vektoren 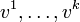 werden nun wie folgt bestimmt:
werden nun wie folgt bestimmt:- Man wähle
![v^k \in {\rm Kern}_{\mathbb{C}}(A-\lambda I)^k \setminus [{\rm Span}_{\mathbb{C}}({\rm Kern}_{\mathbb{C}}(A-\lambda I)^{k-1} \cup M)]](/pictures/dewiki/102/f61b3d59846adfa7919bfd5ae9e59b93.png) beliebig, worin M die Menge der zuvor berechneten Spalten (d. h. Basisvektoren) der Stufe k aus zuvor abgearbeiteten Jordanblöcken zum selben Eigenwert λ (sofern vorhanden) bezeichnet. Insbesondere an dieser relativ freien Wahl erkennt man, dass die Basistransformation nicht eindeutig sein kann. Wenn m(λ) = 1 ist v1 der Eigenvektor zum Eigenwert λ.
beliebig, worin M die Menge der zuvor berechneten Spalten (d. h. Basisvektoren) der Stufe k aus zuvor abgearbeiteten Jordanblöcken zum selben Eigenwert λ (sofern vorhanden) bezeichnet. Insbesondere an dieser relativ freien Wahl erkennt man, dass die Basistransformation nicht eindeutig sein kann. Wenn m(λ) = 1 ist v1 der Eigenvektor zum Eigenwert λ. - Nach der Wahl obigen Vektors besteht jedoch keinerlei Wahlfreiheit mehr, man muss sukzessiv vj: = (A − λI)vj + 1 für alle
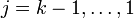 setzen.
setzen.
Nachdem man auf obige Weise alle Jordanblöcke abgearbeitet hat, wurden am Ende alle Spalten von P aufgefüllt. Es gilt: P ist regulär und erfüllt P − 1AP = J, und ihre Spalten bilden eine Basis, bezüglich derer A die Darstellung J besitzt.
Wird die alternative Darstellung der Jordanblöcke gewählt, d.h. mit 1 in der unteren Nebendiagonalen, muss lediglich die Reihenfolge der Basivektoren pro Jordanblock umgekehrt werden.
Beispiel
Als erläuterndes Beispiel betrachte man hierzu die Matrix
wie oben. Es gilt
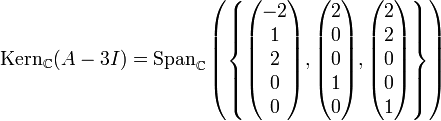 und
und 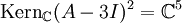 .
.
Ihre Jordannormalform lautet
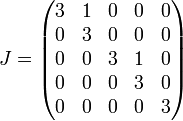 .
.
Man beginne mit dem ersten Jordanblock der Dimension 2. Dazu wähle man
beliebig, beispielsweise
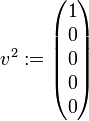 . Dann ist
. Dann ist 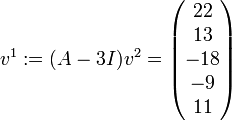 zu wählen. Daraus erhält man
zu wählen. Daraus erhält man 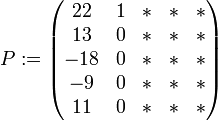 . Nun gehe man zum zweiten Jordanblock der Größe 2 über. Man wähle nun
. Nun gehe man zum zweiten Jordanblock der Größe 2 über. Man wähle nunbeliebig, beispielsweise
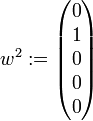 . Dann ist
. Dann ist 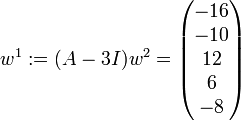 , und man landet bei
, und man landet bei 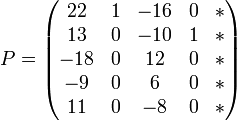 . Schließlich ist der letzte Jordanblock (der Größe 1) an der Reihe. Man wähle hierzu
. Schließlich ist der letzte Jordanblock (der Größe 1) an der Reihe. Man wähle hierzubeliebig, beispielsweise
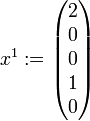 . Dann ist
. Dann ist 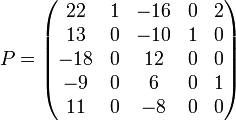 eine reguläre Matrix mit J = P − 1AP.
eine reguläre Matrix mit J = P − 1AP.Der ineffiziente Ansatz hätte für dieses Beispiel unter anderem ein Gleichungssystem mit 25 Variablen lösen müssen.
Reelle jordansche Normalform
Betrachtet man reelle Matrizen, so zerfällt deren charakteristisches Polynom im Allgemeinen nicht mehr vollständig in Linearfaktoren, sondern nur noch in irreduzible Faktoren, die in diesem Fall stets lineare oder quadratische Faktoren sind. Es stellt sich nun die Frage nach einer Normalform, wenn man ausschließlich reelle Basistransformationen zulässt.
Zu einem quadratischen irreduziblen Faktor
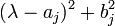 mit bj > 0 definiert man als Jordanblock
mit bj > 0 definiert man als JordanblockWir nennen die Anzahl der Zeilen (bzw. Spalten) die Größe dieses Blocks. Dann bezeichnet man
als reelle jordansche Normalform. Um sie und eine geeignete reelle Matrix
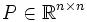 zu bestimmen, kann man folgendermaßen vorgehen:
zu bestimmen, kann man folgendermaßen vorgehen:- Bestimme das charakteristische Polynom und faktorisiere es in irreduzible Faktoren. Es ergibt sich
-
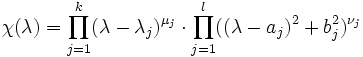 ,
,
- wobei
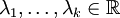 paarweise verschiedene Eigenwerte mit Vielfachheit
paarweise verschiedene Eigenwerte mit Vielfachheit 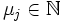 bezeichnen. Weiter seien darin
bezeichnen. Weiter seien darin 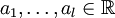 ,
,  ,
, 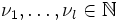 und
und  paarweise verschieden.
paarweise verschieden.
- Für jedes
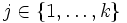 bestimme man
bestimme man
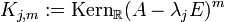 für
für 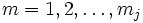 ,
,- worin
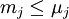 die kleinste natürliche Zahl ist mit
die kleinste natürliche Zahl ist mit 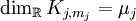 . Analog bestimme man für jedes
. Analog bestimme man für jedes 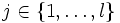
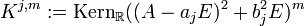 für
für 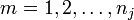 ,
,- worin
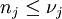 die kleinste natürliche Zahl ist mit
die kleinste natürliche Zahl ist mit 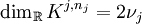 .
. - Zudem setzen wir Kj,0: = Kj,0: = {0}.
- Nun stelle man die jordansche Normalform auf. Es gilt hierbei
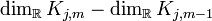 ist die Anzahl der Jordanblöcke zum Eigenwert λj, deren Größe größer oder gleich m ist.
ist die Anzahl der Jordanblöcke zum Eigenwert λj, deren Größe größer oder gleich m ist.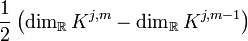 ist die Anzahl der Jordanblöcke zum Faktor
ist die Anzahl der Jordanblöcke zum Faktor 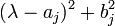 , deren Größe größer oder gleich 2m ist.
, deren Größe größer oder gleich 2m ist.
- Außerdem ist μj die Summe der Jordanblockgrößen zum Eigenwert λj und 2νj die Summe der Jordanblockgrößen zum Faktor
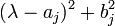 . Aus diesen Angaben kann man eindeutig die jordansche Normalform J bestimmen.
. Aus diesen Angaben kann man eindeutig die jordansche Normalform J bestimmen.
- Danach bestimme man die Basistransformationsmatrix P, das heißt, man sucht eine reelle invertierbare Matrix
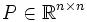 , so dass J = P − 1AP.
, so dass J = P − 1AP.
Ein Verfahren, um eine Basistransformation zu erhalten, ist das folgende:
- Man arbeite die Blöcke nacheinander ab. Dabei ist zu beachten, dass man bei Jordanblöcken zum selben irreduziblen Faktor stets vom größten Block zum kleinsten Block vorgeht. Zu jedem Block der Größe t werden t Spalten der Basistransformationsmatrix
 nach einem bestimmten Schema bestimmt. Wenn der Block in J die Spalten
nach einem bestimmten Schema bestimmt. Wenn der Block in J die Spalten 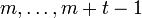 belegt, so werden die Vektoren
belegt, so werden die Vektoren  in P ebenso (von links nach rechts) in die Spalten
in P ebenso (von links nach rechts) in die Spalten 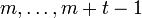 eingefügt. Die Vektoren
eingefügt. Die Vektoren  werden nun wie folgt bestimmt:
werden nun wie folgt bestimmt:
- Zu einem Jordanblock der Größe m zum Eigenwert λj wähle man
![v^m \in K_{j,m} \setminus [{\rm Span}_{\mathbb{R}}(K_{j,m-1} \cup M)]](/pictures/dewiki/100/d73afb110acb0afd147aac8685be2f9f.png) beliebig, worin M die Menge der zuvor berechneten Spalten (das heißt Basisvektoren) der Stufe m aus zuvor abgearbeiteten Jordanblöcken zum selben Eigenwert λ (sofern vorhanden) bezeichnet. Anschließend setze man sukzessiv vt − 1: = (A − λjE)vt für alle
beliebig, worin M die Menge der zuvor berechneten Spalten (das heißt Basisvektoren) der Stufe m aus zuvor abgearbeiteten Jordanblöcken zum selben Eigenwert λ (sofern vorhanden) bezeichnet. Anschließend setze man sukzessiv vt − 1: = (A − λjE)vt für alle 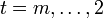 .
. - Zu einem Jordanblock der Größe 2m zum irreduziblen Faktor
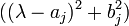 wähle man einen Vektor
wähle man einen Vektor ![v^{2m} \in K^{j,m} \setminus [{\rm Span}_{\mathbb{R}}(K^{j,m-1}\cup M)]](/pictures/dewiki/56/8a7c462af5f6b66d96fd1f583253a7c0.png) , wobei M aus den bereits berechneten Hauptvektoren der Stufen 2m,2m − 1 zum selben irreduziblen Faktor
, wobei M aus den bereits berechneten Hauptvektoren der Stufen 2m,2m − 1 zum selben irreduziblen Faktor 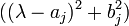 besteht.
besteht.
- Zu einem Jordanblock der Größe m zum Eigenwert λj wähle man
-
- Dann setze man für
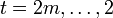 sukzessiv
sukzessiv 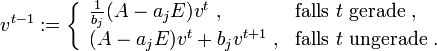
- Schließlich setzt man P wie gehabt aus den Vektoren
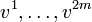 zusammen.
zusammen.
- Dann setze man für
- Nachdem man auf obige Weise alle Jordanblöcke abgearbeitet hat, werden am Ende alle Spalten von P aufgefüllt. Es gilt: P ist regulär und erfüllt P − 1AP = J, und ihre Spalten bilden eine Basis, bezüglich derer A die Darstellung J besitzt.
Beispiel
Man betrachte die Matrix
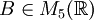 , die wie folgt definiert ist
, die wie folgt definiert istIhr charakteristisches Polynom lautet χ(λ) = ((λ − 2)2 + 1))2(λ − 1), wobei (λ − 2)2 + 1 irreduzibel über
 ist. Nun berechnen wir die jordansche Normalform:
ist. Nun berechnen wir die jordansche Normalform: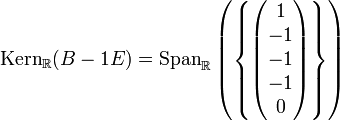 .
.
Dieser Kern hat die Dimension 1. Also gibt es nur einen Jordanblock der Größe
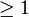 . Andererseits muss die Summe der Jordanblockgrößen 1 sein (die Potenz von λ − 1), so dass es genau einen Jordanblock zum Eigenwert 1 gibt, und er hat die Größe 1. Weiter hat
. Andererseits muss die Summe der Jordanblockgrößen 1 sein (die Potenz von λ − 1), so dass es genau einen Jordanblock zum Eigenwert 1 gibt, und er hat die Größe 1. Weiter hatdie Dimension 2, so dass es demzufolge nur
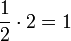 Jordanblock der Größe
Jordanblock der Größe 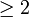 gibt. Da die Summe der Jordanblockgrößen 4 sein muss (das Doppelte der Potenz von (λ − 2)2 + 1), ergibt sich, dass dieser eine Jordanblock die Größe 4 besitzt. Außerdem errechnen wir
gibt. Da die Summe der Jordanblockgrößen 4 sein muss (das Doppelte der Potenz von (λ − 2)2 + 1), ergibt sich, dass dieser eine Jordanblock die Größe 4 besitzt. Außerdem errechnen wir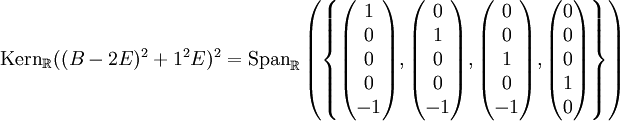 .
.
Somit ist
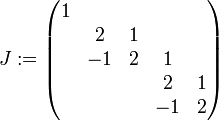 die reelle jordansche Normalform von B.
die reelle jordansche Normalform von B.Zum Vergleich, die komplexe jordansche Normalform lautet
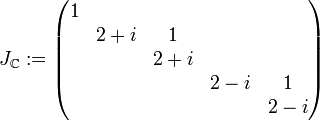 .
.Zum Berechnen einer Basistransformationsmatrix beginne man mit dem ersten reellen Eigenwert und dann mit dem (ersten) Jordanblock der Dimension 1. Man wähle
beliebig, also beispielsweise
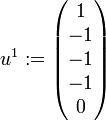 . Daraus erhält man
. Daraus erhält man 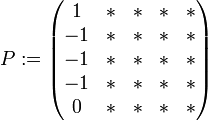 .
.Nun gehe man zum ersten irreduziblen Faktor (komplexen Eigenwert) und dann zum Jordanblock der Größe 4 über. Dazu wähle man
beliebig, beispielsweise
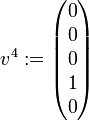 . Dann ist
. Dann ist 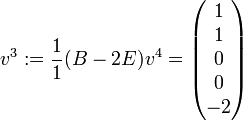 ,
, 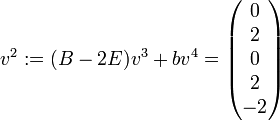 und
und 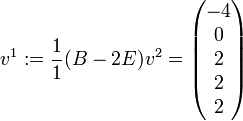 zu wählen. Daraus erhält man:
zu wählen. Daraus erhält man: 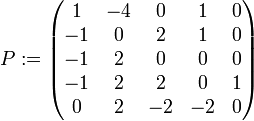 ist eine reguläre Matrix mit J = P − 1BP.
ist eine reguläre Matrix mit J = P − 1BP.Jordansche Normalform in allgemeinen Körpern
Die jordansche Normalform kann noch weiter verallgemeinert werden auf allgemeine Körper. In diesem Zusammenhang wird sie häufig auch als Weierstraß-Normalform (bzw. Frobenius-Normalform) bezeichnet. Dies erlaubt eine eindeutige Matrixdarstellung von Endomorphismen von endlich-dimensionalen Vektorräumen, bei der sich alle ähnlichen Endomorphismen durch eine eindeutige Matrix darstellen lassen. So können ähnliche lineare Abbildungen identifiziert werden. Das Lemma von Frobenius charakterisiert zueinander ähnliche Matrizen durch die Elementarteiler ihrer charakteristischen Matrizen und liefert die Frobenius-Normalform als Normalform des Vektorraums unter der Operation eines Polynomrings.
Durch die Darstellung in der Weierstraß-Normalform ist der Aufbau des Minimalpolynoms sofort erkennbar und das charakteristische Polynom leicht zu berechnen.
Anwendung bei linearen Differentialgleichungssystemen erster Ordnung mit konstanten Koeffizienten
Gegeben sei ein lineares Differentialgleichungssystem (von n Gleichungen) erster Ordnung mit konstanten Koeffizienten
durch eine Matrix
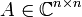 und eine stetige Funktion
und eine stetige Funktion 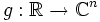 . Es ist bekannt, dass die eindeutige Lösung des Anfangswertproblems
. Es ist bekannt, dass die eindeutige Lösung des Anfangswertproblemsgegeben ist durch
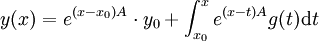 ,
,
worin
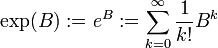 für
für 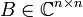
die Matrixexponentialfunktion bezeichnet. Man beachte:
- Die Matrixexponentialfunktion von einem komplexen Jordanblock kann explizit ausgerechnet werden:
-
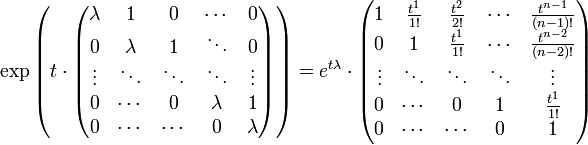 .
.
- Die Matrixexponentialfunktion von einer komplexen Jordannormalform
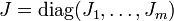 kann explizit berechnet werden mittels:
kann explizit berechnet werden mittels:
-
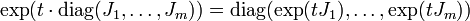 .
.
- Die Matrixexponentialfunktion einer Matrix A, deren komplexe Jordannormalform J zusammen mit einer Basistransformationsmatrix
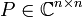 bekannt ist, das heißt A = PJP − 1, kann explizit berechnet werden mittels:
bekannt ist, das heißt A = PJP − 1, kann explizit berechnet werden mittels:
-
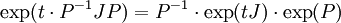 .
.
Mit anderen Worten: Kennt man eine Darstellung A = PJP − 1 mit der komplexen jordanschen Normalform J, so kann man exp(tA) für jedes
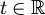 explizit ausrechnen, so dass zum Bestimmen von
explizit ausrechnen, so dass zum Bestimmen vonnur noch das Integrationsproblem zu lösen ist, welches im homogenen Fall g = 0 völlig entfällt.
Siehe auch
- Diagonalisierung ist ein Spezialfall der jordanschen Normalform.
- Die jordansche Normalform ist ein Spezialfall der Weierstraß-Normalform.
- Die Existenz der jordanschen Normalform liefert die Existenz der (additiven) Jordan-Chevalley-Zerlegung eines Endomorphismus.
Literatur
- Herbert Amann: Gewöhnliche Differentialgleichungen. 2. Auflage. Gruyter - de Gruyter Lehrbücher, Berlin/New York 1995, ISBN 3-11-014582-0.
Weblinks
- Daniel Winkler: Kochen mit Jordan. (PDF-Datei)
- Jordan matrix. In: Encyclopaedia of Mathematics. (englisch)
- Jordan canonical form theorem. In: PlanetMath. (englisch)
- The Real Jordan Form. In: Number Theory Web. (englisch)
- Das Gelbe Rechenbuch / Zusätze: Jordanform von Matrizen (PDF-Datei)
Wikimedia Foundation.