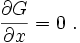Statisches Gleichgewicht

Das Gleichgewicht ist in der Physik allgemein ein sich (zumindest auf eine gewisse Zeit) nicht verändernder Zustand eines Systems. Dieser allgemeine Begriff führt in den verschiedenen Fachbereichen zu unterschiedlichen Betrachtungen:

Mechanik

Grundlagen

Das Gleichgewicht im Sinne der Mechanik ist der Zustand eines Körpers oder eines unbewegten, gekoppelten Systems von Körpern, in dem sich alle angreifenden Kräfte beziehungsweise Momente gegenseitig aufheben. Nach dem ersten Newton’schen Axiom (Trägheitsgesetz) bedeutet dies, dass der Körper entweder in Ruhe verharrt (seine Lage nicht verändert) oder sich gleichförmig weiter bewegt (ohne Beschleunigung).

Betrachtet man statt der vektoriellen Kräfte ein skalares Potential des Gesamtsystems, so beschreibt eine Gleichgewichtslage den Zustand mit extremalen Potential. Der Körper verändert also seine Lage nicht.

Der Teilbereich der Physik, der sich speziell mit Gleichgewichtssituationen beschäftigt, ist die Statik. Gleichgewichtssituationen kommen jedoch allgemein in vielen Bereichen von Physik und Technik vor. Die Betrachtung muss sich auch nicht notwendig auf rein mechanische Kräfte beschränken, etwa können sich Gravitation und elektrische Anziehung ausgleichen. Oft erlauben Gleichgewichte einfache Berechnungen, wo sonst mit komplizierten Differentialgleichungen gearbeitet werden müsste, indem einfach die wirkenden Kräfte gleichgesetzt werden können (nach dem Reaktionsprinzip, dem dritten Axiom des Newton). Außerdem lassen sich Einzelkräfte vielfach auf ihre Resultierende reduzieren (newtonsches Superpositionsprinzip). Des Weiteren lassen sich Systeme in wählbaren Grenzen als abgeschlossen betrachten, und von außen wirkende Kräfte durch Scheinkräfte kompensieren (Prinzip der virtuellen Kräfte oder der äußeren Kraft), wie auch durch Scheinkräfte nicht-inertiale Systeme analog zu inertialen behandeln (d'Alembertsches Prinzip).

Exakt ausgedrückt müssen folgende Bedingungen erfüllt sein, damit ein Körper im Gleichgewicht ist (Gleichgewichtsbedingungen):

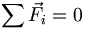1. $\sum \vec F_{i} = 0$ – Die Summe der Resultierenden aller wirkenden Kräfte muss gleich null sein
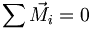2. $\sum \vec M_{i} = 0$ – Die Summe aller Momente um einen beliebigen Punkt muss gleich null sein

bzw.

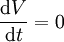$\frac{\mathrm dV}{\mathrm dt} = 0$ – Das Potential V muss extremal sein

In den Summen sind Zwangs- und eingeprägte Kräfte bzw. Momente enthalten.

Die Folgerung der Gleichgewichtsbedingungen ist:

Am starren Körper lassen sich alle statisch bestimmten Aufgaben mit den Gleichgewichtsbedingungen lösen.

Für Systeme miteinander verbundener Körper ist für jeden Körper ein solcher Satz von Gleichgewichtsbedingungen anzusetzen. Um die Elimination der Zwangskräfte aus dem Gleichungssystem zu vermeiden, können an Stelle der Gleichgewichtsbedingungen andere Theoreme der Mechanik verwendet werden, z. B. das Prinzip der virtuellen Arbeit.

Illustration der Gleichgewichtsarten: Pendel

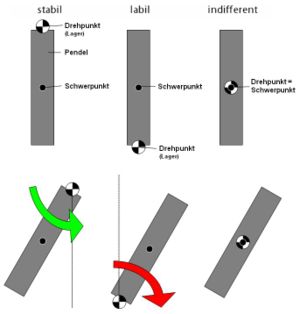
Es werden drei Arten des Gleichgewichts unterschieden:

• Stabiles Gleichgewicht: Bei einer kleinen Auslenkung kehrt der Körper wieder in die vorige Lage zurück. Das Potential besitzt ein Minimum.
• Labiles Gleichgewicht: Der Körper befindet sich momentan im Gleichgewicht, wird bei einer kleinen Auslenkung aber weiter von dieser Lage wegstreben. Das Potential besitzt ein Maximum.
• Indifferentes Gleichgewicht: Der Körper nimmt nach einer kleinen Auslenkung eine neue Gleichgewichtslage ein. Das Potential ändert sich nicht.

Kräftegleichgewicht

Ein Körper befindet sich im Kräftegleichgewicht, wenn die resultierende Vektorsumme der auf ihn wirkenden Kräfte Null ergibt. Dies bedeutet auch, dass er kein Bestreben zeigt, seinen gegenwärtigen Bewegungszustand zu ändern, oder anders ausgedrückt, er wird nicht beschleunigt. In diesem Fall wird sich ein Körper mit gleichmäßiger Geschwindigkeit weiter bewegen, falls er schon in Bewegung war oder in Ruhe bleiben. Dies gilt sowohl für lineare Bewegungen (Translation) als auch für Drehbewegungen (Rotation).

Gleichgewichtslagen: stabil, labil, indifferent

Die drei Arten des mechanischen Gleichgewichts lassen sich für Körper, auf die nur die Gravitation wirkt, durch die Lage von Schwerpunkt und Angriffspunkt des Drehmomentes beschreiben:

• Stabiles Gleichgewicht: Der Schwerpunkt des Körpers befindet sich unterhalb des Drehpunktes (z. B. beim Pendel).
• Labiles Gleichgewicht: Der Schwerpunkt des Körpers befindet sich oberhalb des Drehpunktes (z. B. beim Inversen Pendel).
• Indifferentes Gleichgewicht: Der Schwerpunkt und der Drehpunkt des Körpers fallen zusammen (z. B. beim Rad).

Illustration der Gleichgewichtsarten: Kugel

Eine weitere Veranschaulichung ist die Betrachtung einer Kugel:

• Liegt die Kugel in einer Schüssel, so ist sie im stabilen Gleichgewicht, sie wird bei einer Verschiebung zurückrollen.
• Liegt die Kugel auf einer flachen Kuppe, so ist sie im labilen Gleichgewicht, sie wird bei einer Verschiebung wegrollen.
• Liegt die Kugel auf einer Ebene, so ist sie im indifferenten Gleichgewicht, sie wird an dem Punkt, an den man sie verschiebt, liegenbleiben, bzw. bei einmaliger Krafteinwirkung und unter Vernachlässigung des Reibungswiderstandes in ihrem Bewegungszustand verharren (Massenträgheit).

Siehe auch: Standfestigkeit, Stabilität

Thermodynamik

Die Thermodynamik bezeichnet ein System als im Gleichgewicht, wenn die Entropie des Systems ein Extremum annimmt. Da aber die Entropie minimal Null sein kann (d. h. startet bei Null) kann man das Extremum mit dem Maximum gleichsetzen bzw. als gleichbedeutend annehmen.

Im thermodynamischen Gleichgewicht gilt grundsätzlich das Kräftegleichgewicht aus Gibbs freier Enthalpie:

$\frac{\partial G}{\partial x}=0 \ .$

Das heißt, dass keine Energie- bzw. Potenzialdifferenz zwischen den jeweiligen Punkten im Raum vorliegt.

Ohne innere Barrieren (z. B. Wände) und wirkende Kraftfelder (z. B. Schwerkraft) gilt die triviale Lösung. Sie setzt für zwei beliebige Punkte 1 und 2 des Systems

• das thermische Gleichgewicht (s. u.) T₁ = T₂,
• das mechanische Gleichgewicht (s. o.) p₁ = p₂ und
• das Chemische Gleichgewicht μ₁ = μ₂

voraus. Die Temperatur T, der Druck p sowie das chemische Potenzial μ sind somit im Gleichgewicht überall zeitlich konstant und gleich. Allgemeiner kann man zeigen, dass die Forderung nach maximaler Entropie des Gesamtsystems gleichwertig zur Forderung der Konstanz aller freien intensiven Variablen ist bzw. einem Extremalprinzip bezüglich des zugehörigen thermodynamischen Potenzials entspricht.

Da keine treibenden Gradienten mehr vorliegen, enthält ein System im thermodynamischen Gleichgewicht keine Flüsse, z. B. von Materie, Wärme oder Arbeit. Ein System im thermodynamischen Gleichgewicht ist daher immer stationär.

Der Umkehrschluss gilt jedoch nicht. Ein stationärer Zustand entspricht nicht in jedem Fall einem thermodynamischen Gleichgewicht. In einigen Fällen können durchaus stationäre Flüsse vorliegen: das nennt man das so genannte Fließgleichgewicht.

Ferner ist zu bemerken, dass reversible Prozesse nur entlang nahe beieinander liegender thermodynamischer Gleichgewichtspunkte möglich sind, da andernfalls die Entropie des Systems steigt.

Thermisches Gleichgewicht

Der Begriff thermisches Gleichgewicht wird in zwei verschiedenen Zusammenhängen benutzt.

Zum einen im oben verwendeten Sinne als Zustand eines einzelnen thermodynamischen Systems: Es befindet sich im thermischen Gleichgewicht, wenn es durch einige wenige makroskopische Größen beschrieben werden kann und wenn sich diese Größen zeitlich nicht ändern. Eine Flasche Schnaps im Kühlschrank befindet sich im thermischen Gleichgewicht, weil ihr Zustand durch Masse, Temperatur, Druck und Alkoholgehalt eindeutig bestimmt ist und (oft) über längere Zeit konstant bleibt. Ein Liter kochendes Spaghettiwasser befindet sich nicht im thermischen Gleichgewicht, weil für die Beschreibung seiner turbulenten Strömungsbewegung sehr viele Informationen erforderlich sind und es deshalb im strengen Sinne kein thermodynamisches System ist.

Zum anderen als Beziehung zwischen mehreren Systemen: Zwei Körper, die miteinander in thermischem Kontakt stehen, befinden sich miteinander genau dann im thermischen Gleichgewicht, wenn sie die gleichen Temperaturen besitzen. Ist ein System A sowohl mit einem System B als auch mit einem System C im thermischen Gleichgewicht, dann sind auch die Systeme B und C miteinander im thermischen Gleichgewicht. Diese Aussage bildet eine wichtige Grundannahme der Thermodynamik und wird zuweilen als Nullter Hauptsatz der Thermodynamik bezeichnet.

Lokales thermisches Gleichgewicht

Im thermischen Gleichgewicht stehen alle Prozesse im Gleichgewicht. Dies fordert u. a. auch, dass die Rate der Emission und Absorption von Strahlung im Gleichgewicht steht. Wenn das Strahlungsspektrum dem eines schwarzen Hohlraumstrahlers entspricht, gilt das thermische Gleichgewicht.

In vielen Fällen ist die Emissions- und Absorptionsrate jedoch selektiv; die Strahlung von Gasen und Flüssigkeiten sind über einen weiten Wellenlängenbereich optisch dünn, da nur bestimmte Energiezustände entsprechend der Quantenzahlen erlaubt sind. Gase oder Flüssigkeiten sind transparent für die Strahlung, deren Energie nicht zu einer Strahlungsanregung der Teilchen führen kann.

Mit dem lokalen thermodynamischen Gleichgewicht (engl. local thermodynamic equilibrium - Abkürzung LTE) wird das Verhältnis von angeregten zu nichtangeregten Molekülen beschrieben, das von der Temperatur und der Strahlungsintensität abhängt. Im isothermen Gleichgewicht von Strahlung und Molekülanregung wird dieses Verhältnis durch die Boltzmann-Statistik beschrieben. Wenn keine isothermen Bedingungen vorliegen, entstehen Abweichungen von der Boltzmann-Statistik. Sind diese Abweichungen gering, was hauptsächlich bei hoher Stoßhäufigkeit der Gasmoleküle der Fall ist, sind die Abweichungen zwischen der Boltzmann-Statistik und dem realem Verhältnis sehr gering, so daß man vom lokalen thermodynamischen Gleichgewicht spricht.

Dieser Fall des LTE liegt z. B. im größten Bereich der Erdatmosphäre vor. Erst in sehr großen Höhen, wo wegen des geringen Drucks die Stoßhäufigkeiten sehr gering sind, werden die Abweichungen von der Boltzmann-Statistik wesentlich und es liegt kein LTE mehr vor.

Hydrodynamik

In der Strömungslehre stellt sich das hydrostatische Gleichgewicht als Ausgleich einer gerichteten Kraft auf einen Körper und eines Druckgradienten in dem umgebenden Fluid dar.

In erweitertem Sinne können aber auch Teile des Fluids selbst zu Paketen zusammengefasst und wie ein Körper behandelt werden. Hierbei findet ein Ausgleich zwischen den mechanischen und den thermodynamischen Aspekten des Systems statt. Damit untersucht man etwa Konvektion und deren Gleichgewichtslagen, oder in der Meteorologie die Schichtungsstabilität der Erdatmosphäre.

Dynamisches Gleichgewicht

Auch über die hier beschriebenen statischen Zustände hinaus findet der Gleichgewichtsbegriff Anwendung. Ein dynamisches Gleichgewicht liegt stets dann vor, wenn in einem System zwei entgegengesetzt verlaufende Prozesse sich in ihrer Wirkung gerade aufheben.

Der Gleichgewichtsbegriff in der Chemie ist somit typischerweise dynamisch zu verstehen, etwa als Fließgleichgewicht.

Beispiele aus der Physik:

• Das Strahlungsgleichgewicht zweier unterschiedlich heißer Körper in einem abgeschlossenen System mit Emission und Absorption von Wärmestrahlung, näheres siehe unter Prevostscher Satz.
• Die Ausbreitung von Wellen über ein dispersives und nichtlineares Medium. Ein dynamisches Zusammenspiel dieser Eigenschaften kann zu vielzahligen Phänomenen führen, z. B. zu einer Herausbildung sog. Solitonen.

Siehe auch: D'Alembertsches Prinzip, Kritischer Punkt (Dynamik)