Steckhalma

Solitär (auch Solitaire, Steck- oder Solohalma, Springer, Jumper, Nonnenspiel, Einsiedlerspiel) ist ein Brettspiel für eine Person. Das weitest verbreitete Spielfeld ist kreuzförmig und wird mit 32 Steinen auf 33 Feldern gestartet. Es wird auch als Englisches Solitär bezeichnet (Bild).

Da zumindest in den USA auch das Kartenspiel Patience Solitaire heißt, nennt man das Brettspiel auf Englisch eher Peg Solitaire oder Sailor's Solitaire, in den USA nach einer bekannten Marke auch Hi-Q.

Geschichte

1687: die Prinzessin von Soubise

Dass das Spiel zuerst in Frankreich bekannt war, ist gesichert. Es taucht erstmals 1687 auf einem Porträt von Claude-Auguste Berey auf und wurde mit Sicherheit am Hof des Sonnenkönigs gespielt. In England wird es erstmals 1746 erwähnt.

Die Geschichte vom „französischen Adeligen im Gefängnis“ entstammt einem englischen Buch aus dem Jahr 1801, wie John Beasley im einzigen (und vergriffenen) Fachbuch zum Thema, The Ins and Outs of Peg Soitaire, festhält. Seit 1985 verweist Beasley diese Geschichte in das Reich der „unausrottbaren Fabeln“, mit entsprechend geringem Erfolg. Auch, dass es in Übersee erfunden worden sein könnte, ist weder auszuschließen noch überprüfbar. Die englische Bezeichnung Sailor's solitaire könnte dies andeuten.

In der Schweiz wird dieses Brettspiel weitläufig als „Amdener Tubbeli Spiel“ bezeichnet. Amden ist ein Dorf am Walensee. Handwerker in Amden stellen solche Brettspiele her.

Gottfried Wilhelm Leibniz schätzte das Spiel und erwähnte 1710 in einem Brief, dass er dafür seine eigene Variante gefunden hatte.

Eines der ältesten gedruckt vorliegenden Spielbretter ist kreuzförmig, hat 45 Felder und stammt von J. C. Wiegleb, 1779.

Regeln

Es geht darum, pro Sprung einen Spielstein genau einen daneben liegenden überspringen zu lassen, der dadurch „gelöscht“ wird. Steine dürfen nur in Zeilen und Spalten, nicht jedoch diagonal springen. Nur ein Stein soll übrig bleiben, und dies an einem vorgegebenen Platz, meist in der Brettmitte.

Solitär zu zweit

Das Spiel kann auch zu zweit gespielt werden, wenngleich man dies kaum praktiziert. Die Gegner ziehen abwechselnd. Verlierer ist, wer nicht mehr springen kann.

Brett-Varianten

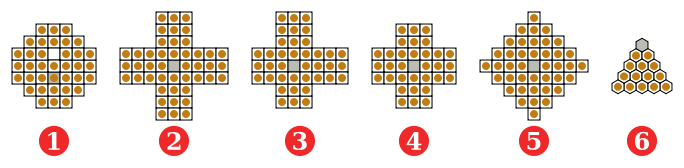
Notation der Züge z. B. bei Beasley. Andere notieren (Zeile,Spalte) in Zahlen, nutzen kartesische Koordinaten oder zählen die Felder der Reihe nach.

Verschiedenste Brettformen kommen vor: Neben dem üblichsten voll symmetrischen „Englischen“ Solitär (4), und der ursprünglichen Form, dem „französischen“ Solitär (1), gibt es unterschiedliche Kreuze, z. B. das deutsche Wiegleb-Brett mit 45 Feldern aus dem Jahr 1779 (2), Kreuze mit unterschiedlich langen Armen (3-3-2-2) (3), Quadrate wie den Diamond mit 41 Feldern (5), 6 × 6 und 8 × 8-Bretter (die natürlich kein Mittelfeld haben können), 9 × 9-Bretter, Dreieck-Versionen (am häufigsten mit 15 Feldern; 6) und etliche mehr – auch sternförmige Anordnungen wurden gespielt.

Für seine Forschungen entwickelte insbesondere George Bell neue Sonderformen, wie etwa Rhomben, das pilzförmige mushroom board mit 36 Feldern, und ähnliche, mit 75 und 90 Feldern.

Das englische Standard-Brett (33 Felder, Abbildung 4)

• Das Standard-Spiel besteht darin, auf einem 33er-Brett alle Felder außer einem mit Steinen zu besetzen. Das zu Spielbeginn freie Feld und das Ziel liegen meist in der Mitte (d4 → d4).
• Das Spiel auf diesem Brett ist jedoch aus jeder Startkonstellation mit einem freien Feld lösbar.

Das Französische Brett (37 Felder, Abbildung 1)

• Die Aufgabe d4 → d4, „Freier Platz…Mitte, letzter Stein…Mitte“ ist im 37er-Brett bewiesenermaßen nicht lösbar, was stark dafür spricht, dass dieses Spiel ursprünglich auch diagonale Züge erlaubte (was nämlich auch diese Aufgabe lösbar macht). Bei den heute üblichen Zügen bleiben zwei Steine übrig, wenn zu Spielbeginn nur das Mittelfeld frei war.

• Nur drei Start-Konstellationen (und deren gedrehte und/oder gespiegelte Gegenstücke) sind auf diesem Brett überhaupt bis zu einem einzelnen Reststein spielbar, nämlich die mit dem freien Platz auf c1 oder d3 oder d6.^[1]

• Literatur zu diesem älteren, in Frankreich übrigens europäisch genannten, Brett ist bedeutend spärlicher als zum 33er.

Andere Versionen des Spiels

• In manchen Varianten sollen aus unterschiedlichsten Start-Konfigurationen bestimmte Zielkonfigurationen erzeugt werden, es ist etwa eine „Pyramide“ oder ein „Kreuz“ abzubauen oder zu erstellen.
• Die besondere Spielweise von Gottfried Wilhelm Leibniz bestand darin, die „Löcher“ anstelle der Steine „springen“ zu lassen.

Computerprogramme

Lösungen können mit Hilfe von Computerprogrammen gefunden werden. Eine grundsätzlich gut geeignete Methode ist „rekursives Backtracking“. Werden dabei alle Möglichkeiten systematisch durchprobiert, dann lässt sich damit auch überprüfen, ob es für eine bestimmte End-Stellung überhaupt eine Lösung aus einer bestimmten Ausgangs-Stellung gibt.

Da es für dieselbe Aufgabe meist eine Vielzahl von Lösungen gibt, liegt die letzte Herausforderung darin, die Lösung mit den wenigsten „Zügen“ zu finden (was bedeutet, dass derselbe Stein mehrmals unmittelbar hintereinander springen muss). Die nachgewiesen kürzestmögliche Lösung für das Standardspiel auf dem 33er-Brett, d4 → d4, wurde bereits 1912 vom Spiel-Guru Ernest Bergholt gefunden: 18 „Züge“ (nummeriert von oben links: 15-17, 28-16, 21-23, 24-22, 26-24, 33-25, 18-30, 31-33-25, 09-23, 01-09, 06-18-30-28-16-04, 07-21-23-25, 13-11, 10-12, 27-13-11, 03-01-09, 08-10-12-26-24-10, 05-17).

Die derzeit optimalen Programme zur Lösung von Solitär(Spiel)-Aufgaben wurden ab 2003 von Jean-Charles Meyrignac und George Bell vorgestellt. Meyrignac hat allein für die Startkonstellation „Freies Feld=c1“ auf dem 37er-Brett 280 unterschiedliche Lösungen errechnet (und dabei bewiesen, dass diese Aufgabe nur 20 „Züge“ erfordert).

Anmerkung zum Begriff „Zug“

Zwar wäre es sinnvoll, wie etwa Jürgen Köller es tut, mit „Zug“ nur zu bezeichnen, was man auch Zugserie oder ähnlich nennen könnte, und den „Einzelzug“ stets nur Sprung zu nennen, der allgemeine Sprachgebrauch ist aber anders (man denkt an Schach und andere Brettspiele). In diesem Artikel bedeutet nur „Zug“ in Anführungszeichen mehrere unmittelbar aufeinander folgender Sprünge mit demselben Stein. Bergholts 18 „Züge“ bestehen selbstverständlich aus 31 Sprüngen, Meyrignacs 20 „Züge“ aus 35 Sprüngen.

Nachweise

1. ↑ Beasley, 2003

Weblinks

• http://mathematische-basteleien.de/solitaer.htm (Jürgen Köller)
• http://www.geocities.com/gibell.geo/pegsolitaire/ George Bell, 2006. (Engl.)
• The Games and Puzzles Journal #28, September 2003 (Sonderausgabe, zusammengestellt von John Beasley unter Mitwirkung von Meyrignac, Bell und anderen; Englisch).
• Solitaire, Alle symmetrischen Endpositionen Helmut Strasser, 2005. Die erste und einzige vollständige Sammlung aller symmetrischen Endpositionen des Solitairespiels.