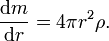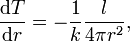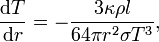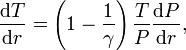Stellare Struktur

Dieser Artikel oder Abschnitt bedarf einer Überarbeitung. Näheres ist auf der Diskussionsseite angegeben. Hilf mit, ihn zu verbessern, und entferne anschließend diese Markierung.

Der innere Aufbau von Sternen hängt von ihrer Masse und ihrem Alter ab. Stellare Strukturmodelle beschreiben die innere Struktur eines Sterns im Detail und stellen die Verbindung her zwischen der Energieerzeugung durch Kernfusion im Zentrum des Sterns und den beobachtbaren Größen wie Leuchtkraft und Spektralklasse. Sie liefern auch Prognosen zur Entwicklung von Sternen.

Energietransport innerhalb des Sterns

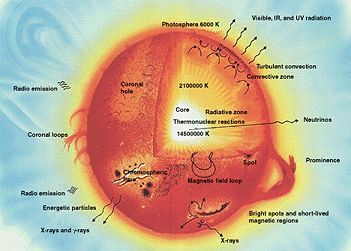Diese Grafik zeigt einen Querschnitt durch einen sonnenähnlichen Hauptreihenstern. NASA image

Schema des Energietransports in massearmen, sonnenähnlichen und massereichen Sternen. Die roten Blitze stellen Energietransport über Strahlung dar, die Ovale mit Pfeilen den Energietransport über Konvektion.

Die im Zentrum des Sterns durch Kernfusion frei gesetzte Energie wird auf unterschiedliche Weise durch die äußeren Schichten eines Sternes transportiert. Konvektion bezeichnet den Energietransport durch großräumige Materiebewegungen: Blasen von heißem Gas steigen im Stern auf und geben Wärme in weiter außen gelegenen Schichten ab, während gleichzeitig kühlere Gaspakete nach unten sinken. Strahlungstransport bezeichnet den Energietransport durch Photonen, die nach außen diffundieren. Bei Weißen Zwergen spielt auch Wärmeleitung eine Rolle.

Wenn die Temperatur schnell genug nach außen hin abfällt, ist Konvektion die dominierende Form des Energietransports.^[1] In Regionen mit kleinerem Temperaturgradient und einer kleinen Opazität (die also durchlässig für Strahlung sind), ist der Energietransport durch Strahlung die dominierende Form.

Die innere Struktur eines Hauptreihensterns wird vor allem durch die Masse des Sterns bestimmt.

In Sternen mit 0,3 bis 1,5 Sonnenmassen findet die Fusion von Wasserstoff zu Helium vor allem über die Proton-Proton-Kette statt, welche keinen steilen Temperaturgradient erzeugt. Somit dominiert die Wärmestrahlung im Innern von sonnenähnlichen Sternen. Im äußeren Teil herrscht dagegen die Konvektion vor, da hier der Stern kühl genug ist, damit der Wasserstoff neutral ist und somit undurchlässig für ultraviolette Photonen wird. Sonnenähnliche Sterne haben also radiative Kerne und konvektive Hüllen.

In massereichen Sternen (schwerer als ca. 1,5 Sonnenmassen) liegt die Kerntemperatur über etwa 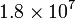$1.8 \times 10^7$ K, so dass die Fusion von Wasserstoff zu Helium vorwiegend über den Bethe-Weizsäcker-Zyklus (auch CNO-Zyklus genannt) geschieht. Im Bethe-Weizsäcker-Zyklus steigt die Energieproduktion mit der 15. Potenz der Temperatur an, während sie bei der Proton-Proton-Kette nur mit der vierten Potenz der Temperatur zunimmt.^[2] Wegen der starken Temperaturempfindlichkeit des CNO-Zyklus entsteht im inneren Teil des Sterns ein Temperaturgradient, der steil genug ist, um den Kern konvektiv zu machen. In den äußeren Schichten des Sterns ist der Temperaturgradient zwar flacher, jedoch bleibt die Temperatur so hoch, dass der Wasserstoff noch fast völlig ionisiert ist, so dass der Stern für ultraviolette Strahlung durchsichtig bleibt. Dadurch haben massereiche Sterne eine Strahlungshülle.

Hauptreihensterne mit kleinen Massen haben keine Strahlungszone; der dominierende Energietransportmechanismus ist im gesamten Stern die Konvektion. Ebenso sind Riesensterne voll konvektiv.^[3]

Gleichungen der stellaren Struktur

Das einfachste Modell für den Aufbau von Sternen ist das kugelsymmetrische quasi-statische Modell. Dieses geht davon aus, dass sich der Stern in einem eingeschwungenen Zustand befindet und nicht rotiert, so dass keine ausgezeichnete Achse vorliegt. Das Modell beruht auf vier grundlegende Differentialgleichungen erster Ordnung: Zwei davon beschreiben, wie Dichte und Druck vom Radius abhängen; zwei weitere beschreiben, wie Temperatur und Leuchtkraft vom Radius abhängen.^[4]

Die physikalischen Größen, die in diesem Modell den Sternaufbau charakterisieren, sind die Dichte ρ(r), die Temperatur T(r), der Gesamtdruck (Materie plus Strahlung) P(r), die Leuchtkraft l(r) und die Energieproduktionsrate pro Masseeinheit ε(r). Zur Ableitung der Gleichungen werden kugelförmige Schalen der Dicke dr im Abstand r vom Mittelpunkt des Sterns betrachtet. Man geht davon aus, dass an jedem Punkt im Stern lokales thermodynamisches Gleichgewicht (LTG) herrscht, so dass die beiden Komponenten Materie und Strahlung (Photonen) die gleiche Temperatur haben. Streng genommen wird das LTG nie genau erreicht, da die Temperatur unterhalb der betrachteten Schicht stets höher ist als die Temperatur darüber. Jedoch ist diese Näherung unter normalen Umständen sehr genau, da die mittlere freie Weglänge der Photonen, λ, klein ist verglichen mit den Strecken, über die sich die Temperatur merklich ändert, d. h. $\lambda \ll T/|\nabla T|$.

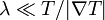Ein stabiler Stern befindet sich im hydrostatischen Gleichgewicht: Die nach außen gerichtete Kraft auf eine gegebene Kugelschale, die sich aus dem nach außen abfallenden Druck ergibt, steht in exakter Balance mit der innen gerichteten Kraft infolge der gravitativen Anziehung durch die weiter innen liegenden Schichten:

${\mbox{d} P \over \mbox{d} r} = - { G m \rho \over r^2 }$.

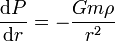Dabei ist m(r) die Masse, welche innerhalb der betrachteten Schale bei r liegt; G ist die Gravitationskonstante. Die Masse einer Kugelschale ist gegeben durch

${\mbox {d} m \over \mbox{d} r} = 4 \pi r^2 \rho .$

Durch Integration vom Zentrum (r = 0) bis zum Radius r der betrachteten Kugelschale erhält man die eingeschlossene Masse m(r), Integration bis zum äußeren Rand des Sterns(r = R) ergibt die Gesamtmasse.

Indem man den Energieerzeugung in einer kugelförmigen Schale betrachtet, erhält man die Energie-Gleichung, eine Kontinuitätsgleichung für die Leuchtkraft:

${\mbox{d} l \over \mbox{d} r} = 4 \pi r^2 \rho ( \epsilon - \epsilon_\nu )$.

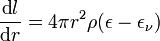Dabei stellt ε_ν die Leuchtkraft pro Masseeinheit dar, die in Form von Neutrinos produziert wird. Neutrinos wechselwirken nur sehr schwach mit gewöhnlicher Materie und entweichen somit aus dem Stern, ohne seine Struktur weiter zu beeinflussen. In Hauptreihensternen wird nur im Zentrum Energie durch Kernreaktionen freigesetzt, so dass in allen äußeren Schalen die Leuchtkraft konstant ist. Bei Sternen in späteren Entwicklungsstadien laufen verschiedene Kernreaktionen auch in Schalen um das Zentrum herum ab (so genanntes „Schalenbrennen“), die in der Energiegleichung berücksichtigt werden müssen.

Die Temperaturverlauf nimmt abhängig von der Art des vorherrschenden Energietransports unterschiedliche Formen an. Für konvektiven Energietransport durch großräumige Materiebewegungen (adäquat für einen Weißen Zwerg) gilt:

${\mbox{d} T \over \mbox{d} r} = - {1 \over k} { l \over 4 \pi r^2 },$

wobei k die Wärmeleitfähigkeit ist.

Im Falle des Energietransports durch Strahlung, adäquat für den inneren Teil eines Hauptreihensterns mit Sonnenmasse und die äußeren Schichten von massereichen Hauptreihensternen, gilt

${\mbox{d} T \over \mbox{d} r} = - {3 \kappa \rho l \over 64 \pi r^2 \sigma T^3},$

wobei κ die Opazität der Materie darstellt und σ die Stefan-Boltzmann-Konstante ist. Die Boltzmannkonstante wurde hierbei auf 1 gesetzt.

Im Falle von konvektivem Leuchtkrafttransport gibt es keine allgemeingültige mathematische Formulierung. Eine vereinfachte heuristische Beschreibung liefert die Mischungswegtheorie. Die Mischungswegtheorie behandelt das Gas in den Sternen in Form von diskreten Elementen, welche jeweils etwa die Temperatur, Dichte und Druck ihrer ursprünglichen Umgebung beibehalten, sich aber über eine charakteristische Strecke, den so genannten Mischungsweg, durch den Stern bewegen.^[5] Für ein einatomiges Ideales Gas ergibt die Mischungswegtheorie

${\mbox{d} T \over \mbox{d} r} = \left(1 - {1 \over \gamma} \right) {T \over P } { \mbox{d} P \over \mbox{d} r},$

wobei γ = c_p / c_v der adiabatische Index ist, das Verhältnis der spezifische Wärmekapazitäten in dem Gas (Für ein vollständig ionisiertes Ideales Gas ist γ = 5 / 3.).

Schließlich wird eine Zustandsgleichung benötigt, welche eine Beziehung zwischen Druck und anderen lokalen Variablen, wie z. B. Temperatur, Dichte, chemische Zusammensetzung, usw., darstellt und somit die Materie, aus der der Stern aufgebaut ist charakterisiert. Für verschiedene Sterntypen und verschiedene Bereiche innerhalb eines Sterns werden unterschiedliche Zustandsgleichungen verwendet, zum Beispiel diejenige für ein ideales Gas, Strahlung oder entartete Materie.

Zusammen mit einer Reihe von Randbedingungen beschreibt eine Lösung der Gleichung das komplette Verhalten eines Sterns. Typischerweise werden als Randbedingungen die Werte der beobachtbaren Parameter an der Oberfläche des Sterns (r = R) und in seinem Zentrum (r = 0) herangezogen: P(R) = 0, d. h. der Druck an der Oberfläche verschwindet; m(0) = 0; dies erfordert, dass die Massendichte ρ im Zentrum nicht divergiert, also endlich bleibt; m(R) = M, die Gesamtmasse des Sterns; und T(R) = T_eff, d.  die Temperatur an der Oberfläche ist gleich der effektive Temperatur des Sterns.

Komplexere Sternaufbaumodelle berücksichtigen weitere Prozesse, zum Beispiel Rotation, durch die die Kugelsymmetrie gebrochen wird, oder Magnetfelder.

Obwohl die heutigen Sternentwicklungsmodelle die Hauptmerkmale des Hertzsprung-Russell-Diagramms beschreiben, müssen sie noch weiter verbessert werden. Es bestehen weiterhin Unsicherheiten, wie der Energietransport innerhalb des Sterns vor sich geht. Die schwierigste Herausforderung bleibt die nummerische Behandlung von Turbulenzen. Einige Forscherteams entwickeln dafür vereinfachte Modelle mit 3D-Berechnungen.

Siehe auch

• Polytrop
• Hauptreihe

Weblinks

• OPAL opacity code
• The Yellow CESAM code, stellar evolution and structure FORTRAN source code
• EZ to Evolve ZAMS Stars a FORTRAN 90 software derived from Eggleton's Stellar Evolution Code, a web-based interface can be found here.
• Geneva Grids of Stellar Evolution Models (some of them including rotational induced mixing)
• The BaSTI database of stellar evolution tracks

Quellen

1. ↑ Carl J. Hansen, Steven D. Kawaler, Virginia Trimble; Springer (Hrsg.): Stellar interiors : physical principles, structure, and evolution. 2. Auflage. 2004, ISBN 0387200894, S. §5.1.1. 
2. ↑ Carl J. Hansen, Steven D. Kawaler, Virginia Trimble; Springer (Hrsg.): Stellar interiors : physical principles, structure, and evolution. 2. Auflage. 2004, ISBN 0387200894, S. Tbl. 1.1. 
3. ↑ Carl J. Hansen, Steven D. Kawaler, Virginia Trimble; Springer (Hrsg.): Stellar interiors : physical principles, structure, and evolution. 2. Auflage. 2004, ISBN 0387200894, S. §2.2.1. 
4. ↑ Diese Erörterung folgte z. B. Michael A. Zeilik, Stephan A. Gregory; Saunders College Publishing (Hrsg.): Introductory Astronomy & Astrophysics. 4. Auflage. 1998, ISBN 0030062284, S. §16-1–16-2.  und Carl J. Hansen, Steven D. Kawaler, Virginia Trimble; Springer (Hrsg.): Stellar interiors : physical principles, structure, and evolution. 2. Auflage. 2004, ISBN 0387200894, S. §7.1. 
5. ↑ Carl J. Hansen, Steven D. Kawaler, Virginia Trimble; Springer (Hrsg.): Stellar interiors : physical principles, structure, and evolution. 2. Auflage. 2004, ISBN 0387200894, S. §5.1. 

Literatur

• R. Kippenhahn, A. Weigert; Springer-Verlag (Hrsg.): Stellar Structure and Evolution. 1990. 
• Carl J. Hansen, Steven D. Kawaler, Virginia Trimble; Springer (Hrsg.): Stellar Interiors. 2. Auflage. 2004, ISBN 0387200894. 
• Achim Weiss, Wolfgang Hillebrandt, Hans-Christoph Thomas, H. Ritter; Cambridge Scientific Publishers (Hrsg.): Cox and Giuli's Principles of Stellar Structure. 2004. 
• Michael A. Zeilik, Stephan A. Gregory; Saunders College Publishing (Hrsg.): Introductory Astronomy & Astrophysics. 4. Auflage. 1998, ISBN 0030062284.