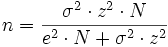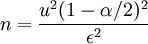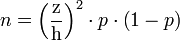Stichprobentechnik

Als Stichprobe bezeichnet man eine Teilmenge einer Grundgesamtheit, die unter bestimmten Gesichtspunkten ausgewählt wurde. Mit Stichproben wird in Anwendungen der Statistik (etwa in der Marktforschung, aber auch in der Qualitätskontrolle und in der naturwissenschaftlichen, medizinischen und psychologischen Forschung) häufig gearbeitet, da es oft nicht möglich ist, die Grundgesamtheit, etwa die Gesamtbevölkerung oder alle hergestellten Exemplare eines Produkts, zu untersuchen. Grundgedanke der Zuhilfenahme von Stichproben ist das Induktionsprinzip, bei dem von besonderen auf allgemeine Fälle geschlossen wird.

Stichprobenumfang

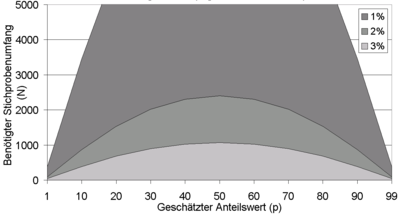Benötigte Stichprobenumfänge bei einfacher Zufallsauswahl

Der Stichprobenumfang (oft auch Stichprobengröße genannt) ist die Anzahl der für eine Prüfung benötigten Proben einer Grundgesamtheit, um statistische Kenngrößen mit einer bestimmten Qualität (Repräsentativität) zu ermitteln (Schätzen). Durch eine geeignete Wahl des Stichprobenumfangs sollen systematische Fehler vermieden und statistisch belegbar werden.

Der Stichprobenumfang wird häufig durch Normen festgelegt, aber auch Erfahrungswerte werden zur Festlegung herangezogen.

Mit den ermittelten Ergebnissen werden statistische Werte berechnet.

Ein Instrument zur Ermittlung von statistischen Werten ist zum Beispiel die Qualitätsregelkarte. Die Standardabweichung und die Prozessfähigkeit sind typische Werte, die bei immer wiederkehrenden Stichproben berechnet werden.

Beim Schätzen werden die Punktschätzung und die Intervallschätzung unterschieden. Während die Punktschätzung für einen gesuchten Parameter einen einzelnen Wert liefert, werden bei der Intervallschätzung auch Informationen über mögliche Abweichungen (Konfidenzintervall) des aus der Probe berechneten Parameters gegenüber dem tatsächlichen Wert der Grundgesamtheit geliefert.

Berechnung der Mindestgröße einer Stichprobe bei gegebenem Konfidenzintervall und gegebenem absoluten Fehler

• $n=\frac{\sigma^2 \cdot z^2 \cdot N}{e^2 \cdot N + \sigma^2 \cdot z^2}$

mit e: Absoluter Fehler = halbe Länge des Konfidenzintervalls

Formel für die Mindestgröße einer Stichprobe für relative Häufigkeiten

• $n = \frac{u^2(1-\alpha/2)^2}{\epsilon^2}$

Um den erforderlichen Stichprobenumfang festlegen zu können sind vorab zu wissen:

• α: Signifikanzniveau, bestimmt das Konfidenzintervall, z. B. bei α = 0,1 für 10 % maximal zulässige Irrtumswahrscheinlichkeit hieße es, dass der kritische Wert bei (1 − α / 2) = 0,95 also 95 %-Grenze lege. Im Falle einer Normalverteilung zx = z(0,95) = 1,645.
• ε: Genauigkeit der Stichprobenergebnisse (zugelassener Fehler, z. B. 0,01 für 1 %)
• u: Standardabweichung der Mittelwerte der Stichproben

Formel für die Mindestgröße einer Stichprobe für Anteilswerte

• $n = \left(\frac{\mathrm{z}}{\mathrm{h}}\right)^2 \cdot p \cdot \left(1-p\right)$

mit

p: geschätzter wahrer Anteil

z: Konfidenzintervall (z. B. 1,96)

h: Präzision der Schätzung (z. B. 0,01)

Beispiel

In der Werkstoffprüfung ist ein Stichprobenumfang von 10 pro 1000 produzierten Teilen durchaus üblich. Er ist u. a. von der Sicherheitsrelevanz des Bauteils oder des Werkstoffes abhängig. Bei den zerstörenden Prüfungen wie zum Beispiel beim Zugversuch wird versucht, den Prüfaufwand und somit die Stichprobe möglichst klein zu halten. Bei der zerstörungsfreien Prüfung z. B. bei Bildverarbeitungssystemen für die Vollständigkeitsprüfung wird häufig eine 100 %-Kontrolle durchgeführt, um Fehler in der Produktion möglichst schnell zu erkennen.

Stichproben in der mathematischen Statistik

In der mathematischen Statistik werden Stichproben idealisierend als Realisierungen von Tupeln 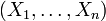$(X_1, \dots, X_n)$ von unabhängig und identisch verteilten Kopien X₁ bis X_n einer Zufallsvariable X betrachtet. In diesem Zusammenhang werden solche Tupel selbst als Stichproben bezeichnet, so zum Beispiel in den Bezeichnungen Stichprobenmittel und Stichprobenvarianz.

Abhängige und unabhängige Stichproben

Sollen zwei Stichproben mittels statistischer Tests miteinander verglichen werden, so muss zwischen abhängigen und unabhängigen Stichproben unterschieden werden:

• Abhängige Stichproben: Elemente von zwei (oder mehr) Stichproben können einander jeweils paarweise zugeordnet werden. Beispiel: Stichprobe 1 besteht aus Personen vor der Behandlung mit einem bestimmten Medikament, und soll verglichen werden mit Stichprobe 2, welche aus den gleichen Personen nach der Behandlung besteht.

• Unabhängige Stichproben: Es besteht kein Zusammenhang zwischen den Elementen der Stichproben. Dies ist beispielsweise der Fall, wenn die Elemente der Stichproben jeweils aus unterschiedlichen Population kommen (z. B. Stichprobe 1 besteht aus Frauen, Stichprobe 2 aus Männern), oder wenn Personen nach dem Zufallsprinzip in zwei oder mehrere Gruppen aufgeteilt werden.

Auswahlverfahren

Um die einzelnen Elemente einer Stichprobe zu erhalten, stehen verschiedene Auswahlverfahren zur Verfügung. Die korrekte Wahl des Auswahlverfahrens ist wichtig, da die Stichprobe repräsentativ sein muss, um auf die Grundgesamtheit schließen zu können (siehe dazu z. B. Hochrechnung). Entscheidend ist eine vernünftige Probenahme, die über den Erfolg der Aussage entscheidet. Häufig sind mehrere Tests notwendig um sicherzustellen, dass tatsächlich rational entschieden wurde.

Ein Auswahlverfahren ist die Art und Weise, wie Personen oder Dinge für einen Zweck ausgewählt werden. Die Statistik beschäftigt sich in der Kombinatorik mit grundsätzlich möglichen Auswahlen. In der Empirie werden mehrere Verfahren (Stichprobenverfahren) zur Auswahl einer repräsentativen Stichprobe unterschieden. Die unterschiedlichen Wahrscheinlichkeiten eines Elementes der Grundgesamtheit, je nach Auswahlverfahren in die Stichprobe zu gelangen, nennt man Einschlusswahrscheinlichkeit. Als Auswahlverfahren werden auch kommerzielle Verfahren bezeichnet, die an Repräsentativität nicht interessiert sind. Die tatsächliche Auswahl der Auskunftgebenden erfolgt z. B. mit dem Random-Route-Verfahren und dem Schwedenschlüssel.

In der Empirie dient das Auswahlverfahren (auch Stichprobenverfahren) der Ermittlung einer repräsentativen Stichprobe. Man unterscheidet generell Stufung, Schichtung und Klumpung. Die verschiedenen Typen von Auswahlverfahren können folgendermaßen charakterisiert werden:

Man unterscheidet:

• Zufallsauswahlverfahren: Bei einem Zufallsauswahlverfahren (auch Wahrscheinlichkeitsauswahl, Zufalls-Stichprobe, Zufallsauswahl, Random-Sample) hat jedes Element der Grundgesamtheit die gleiche Wahrscheinlichkeit (größer Null), in die Stichprobe zu gelangen. Das erfordert die vorherige Erstellung eines Gesamtverzeichnisses aller Elemente der Grundgesamtheit. Man unterscheidet einstufige und mehrstufige Zufallsauswahlverfahren. Nur bei Zufallsauswahlen sind streng genommen die Methoden der induktiven Statistik anwendbar.
• Systematische Stichproben Auswahlverfahren, bei denen subjektive Erwägungen die Auswahl der Zielpersonen bestimmen. Es werden Vorinformationen über die auszuwählenden Fälle genutzt. Verallgemeinerungen sind auf der Basis mathematisch-statistischer Modelle bei bewussten Auswahlen nicht möglich.
• Willkürliche Stichproben: Elemente aus der Grundgesamtheit werden (etwa von einem Interviewer) mehr oder weniger willkürlich in die Stichprobe aufgenommen, es liegt ausschließlich im Ermessen des Interviewers oder auch der Untersuchungspersonen selbst.

Literatur

• Josef Bleymüller, Günther Gehlert, Herbert Gülicher: Statistik für Wirtschaftswissenschaftler. 14. Auflage. Vahlen, München 2002, ISBN 3-8006-3115-6 (Kapitel 12 und 13)
• Jürgen Bortz / Nicola Döring (1995): Forschungsmethoden und Evaluation. Berlin u. a.
• Elisabeth Noelle-Neumann / Thomas Petersen (1996): Alle, nicht jeder. München.
• Rainer Schnell / Paul B. Hill / Elke Esser (1999): Methoden der empirischen Sozialforschung. München, Wien.

Siehe auch

• Rückfangmethode
• Schwedenschlüssel, RLD-Verfahren
• Designeffekt
• Messung

Weblinks

• http://www.mathe-online.at/lernpfade/hypothesen_testen/?kapitel=1 - Lernpfad: Stichprobe und Grundgesamtheit
• Online-Lehrbuch Wirtschaftspsychologie auf WPGS.de: Kapitel über Stichproben in der Marktforschung.
• Handout Statistikvorlesung, WU Wien, 2003
• Bestimmung der Stichprobengröße für repräsentative Umfragen
• Tool zur Bestimmung von Stichprobengrößen aufgrund von Mittelwerten oder Anteilswerten