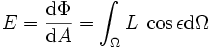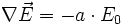Strahlungsstromdichte

Die Bestrahlungsstärke oder Strahlungsstromdichte (engl.: irradiance, heat flux density: Formelzeichen: E) ist der Begriff für die gesamte Leistung der eingehenden elektromagnetischen Energie, die auf eine Oberfläche trifft, bezogen auf die Größe der Fläche. Sie wird normalerweise in Watt pro Quadratmeter gemessen.

Überblick

Die Bestrahlungsstärke ist definiert als der Strahlungsfluss dΦ pro Fläche dA:

$E = \frac{\mathrm{d}\Phi}{\mathrm{d}A} = \int_\Omega L\;\cos\epsilon\mathrm{d}\Omega$

(L=Strahldichte, dΩ=Raumwinkelelement, ε=Winkel des Raumwinkelelementes zur Flächennormalen)

• Formelzeichen: E
• SI-Einheit: Watt pro Quadratmeter
• Einheitenzeichen: W/m²

Anmerkung:

Der Index e – der hier weggelassen ist – bei Formelzeichen in der Photometrie steht für eine energetische Messgröße, die eine objektive Messgröße ist, es fließen nicht die speziellen Eigenschaften der menschlichen Wahrnehmung ein. Im Gegensatz dazu wird der Index v bei Messgrößen gesetzt, bei denen die subjektiven Eigenschaften des menschlichen Auges einfließen, hier steht das v für visuell. Die Entsprechung ist die Beleuchtungsstärke E_v.

Analog zur Bestrahlungsstärke gibt es die spezifische Ausstrahlung, die die von einer Fläche ausgehende Strahlungsleistung pro Fläche bezeichnet.

Die Gershun-Gleichung setzt skalare und vektorielle Bestrahlungsstärke in Bezug.

Spektrale Bestrahlungsstärke

Die spektrale Bestrahlungsstärke E_ν(ν) (Einheit: W m^-2 Hz^-1), der ein Körper ausgesetzt ist, gibt an, welche Strahlungsleistung bei der Frequenz ν aus dem gesamten Halbraum pro Flächeneinheit und pro Einheits-Frequenzintervall auf den Körper trifft:

$E_{\nu}(\nu) = \int_{Halbraum} \, K_{\Omega \nu}(\beta, \varphi, \nu) \, \cos(\beta) \, \mathrm{d}\Omega$.

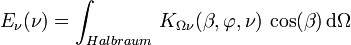• K_Ων ist die spektrale Bestrahlungsdichte.
• Der Kosinusfaktor berücksichtigt den Umstand, dass bei Einstrahlung aus einer beliebigen durch $\varphi$ und β gegebenen Richtung nur die auf dieser Richtung senkrecht stehende Projektion cos(β)dA der Fläche dA als effektive Empfangsfläche auftritt.
• dΩ ist ein Raumwinkelelement: $\mathrm{d}\Omega = \sin(\beta) \, \mathrm{d}\beta \, \mathrm{d}\varphi$.

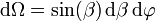Allgemeine Definition im Feld

Für allgemeine, das heißt nicht unbedingt kollimierte, Strahlungsfelder, deren Strahlungsverteilung durch eine Strahldichte L(θ,φ) gegeben ist, ist die Bestrahlungsstärke in Richtung (θ₀,φ₀) definiert als

$E = \int_0^{2\pi}\int_0^{\pi} L(\theta,\phi)\ \vec{e}(\theta_0,\phi_0)\,\vec{e}(\theta,\phi) \ \sin\theta\;{\mathrm{d}\theta}\;{\mathrm{d}\phi}$.

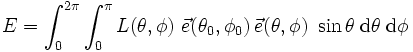Außerdem sind die Größen

• skalare Bestrahlungsstärke (engl.: scalar irradiance) E₀, die die Strahldichte unabhängig von der Richtung berücksichtigt, und
• vektorielle Bestrahlungsstärke (engl.: vectorial irradiance) 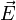$\vec{E}$, die eine Nettobestrahlungsstärke (mit Richtung) darstellt,
  

definiert:

$E_0 = \int_0^{2\pi}\int_0^{\pi} L(\theta,\phi)\ \sin\theta\;{\mathrm{d}\theta}\;{\mathrm{d}\phi}$.

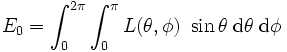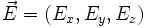$\vec{E} = (E_x, E_y, E_z)$ wobei die Komponenten E_x , E_y und E_z die Bestrahlungsstärken bzgl. der x-, y- bzw. z-Richtung bedeuten.

Gershun-Gleichung

Die Gershun-Gleichung (nach Andre Aleksandrovich Gershun, 1903–1952) setzt die vektorielle und skalare Bestrahlungsstärke in Beziehung zum Absorptionskoeffizienten a:

$\nabla\vec{E} = -a \cdot E_0$

Interessant ist, dass der Streukoeffizient nicht in der Beziehung auftaucht. Dadurch kann der Absorptionskoeffizient a in einer beliebigen Strahlungsverteilung, unabhängig von der Streuung, durch die Bestimmung der beiden Bestrahlungsstärken ermittelt werden.

Literatur

• DIN-Taschenbuch 22. Einheiten und Begriffe für physikalische Größen. Beuth Verlag, 1999, ISBN 3-410-14463-3
• Erich Helbig: Grundlagen der Lichtmeßtechnik. Akademische Verlagsgesellschaft Geest & Portig K.-G., Leipzig 1977
• Gershun, A. (1936/1939): Svetovoe Pole (English: The Light Field), Moskau 1936. Translated by P. Moon and G. Timoshenko (1939) in Journal of Mathematics and Physics, 18, 51-151

Siehe auch:

• Radiometrie
• Fotometrie