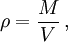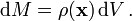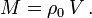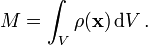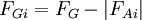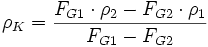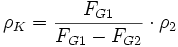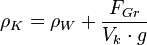Rel. Dichte

Physikalische Größe
Name	Dichte
Formelzeichen der Größe	ρ
Größen- und Einheiten- system Einheit Dimension SI kg·m−3 M·L−3
Siehe auch: Wichte (spezifisches Gewicht), relative Dichte (spezifische Dichte), spezifisches Volumen

Die Dichte (genauer: Massendichte) eines Körpers ist das Verhältnis seiner Masse zu seinem Volumen. Sie wird zum Beispiel in Gramm pro Kubikzentimeter oder Kilogramm pro Liter angegeben. Anschaulich gesagt beschreibt sie, ob der Körper für seine Größe leicht wie eine Feder oder schwer wie ein Stein ist.

Zerteilt man einen Körper, der gleichmäßig aus demselben Material zusammengesetzt ist, dann erhält man Teile mit anderen Massen, anderer Form und anderer Größe. Aber das Verhältnis der Masse M zum Volumen V, die Dichte

$\rho= \frac{M}{V}\,,$

hat bei den Teilen denselben Wert wie bei dem ursprünglichen Körper. Die Dichte ist eine für das Material des Körpers charakteristische, von seiner Form und Größe unabhängige Eigenschaft.

Mit -dichte zusammengesetzte Wörter bezeichnen auch andere Größen, die auf das Volumen, manchmal aber auch auf eine Fläche, eine Länge, ein Frequenzintervall oder Anderes bezogen werden (Beispiele unter Andere Dichtebegriffe unten).

Ortsabhängige Dichte

Bei stetig verteilter Materie ist die Masse dM in einem für kleiner und kleiner werdende Bereiche unabhängig von dV. Der Grenzwert definiert die Massendichte $\rho\,,$

$\mathrm dM = \rho(\mathbf x) \,\mathrm dV\,.$

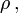
Für einen homogenen Körper, dessen Massendichte in seinerm Inneren überall den Wert ρ₀ hat, ist die Gesamtmasse M das Produkt von Dichte und Volumen $V\,,$

$M = \rho_0\,V\,.$

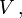
Bei inhomogener Dichte ist die Gesamtmasse allgemeiner das Volumenintegral über die Massendichte

$M = \int_V \rho(\mathbf x)\,\mathrm d V\,.$

Die Dichte ergibt sich aus den Massen der Atome, aus denen das Material besteht und aus ihren Abständen. In homogenem Material, zum Beispiel in einem Kristall, ist die Dichte überall gleich. Sie ändert sich normalerweise mit der Temperatur und, bei Materialien, die wie Gase kompressibel sind, mit dem Druck. Daher ist die Dichte der Atmosphäre ortsabhängig und nimmt mit der Höhe ab.

Der Kehrwert der Dichte wird spezifisches Volumen genannt und spielt vor allem in der Thermodynamik der Gase und Dämpfe eine Rolle. Das Verhältnis der Dichte eines Stoffes zur Dichte im Normzustand wird als Relative Dichte bezeichnet.

Dichtebestimmung durch Auftrieb

Angreifende Kräfte am eingetauchten Körper

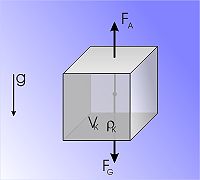
Nach dem Prinzip von Archimedes erfährt ein vollständig in einer Flüssigkeit oder Gas eingetauchter Körper eine Auftriebskraft, die der Gewichtskraft des Volumens der verdrängten Flüssigkeit entspricht. Um die zwei Unbekannten Dichte und Volumen zu bestimmen, sind zwei Messungen erforderlich.

Taucht man einen beliebigen Körper mit dem Volumen V_K vollständig in zwei Flüssigkeiten oder Gase mit den bekannten Dichten ρ₁ und ρ₂ ein, so erfährt er die unterschiedlichen, resultierenden Gewichtskräfte F_G1 bzw. F_G2. Messbar sind die resultierenden Kräfte mittels einer einfachen Waage. Die gesuchte Dichte ρ_K lässt sich wie folgt bestimmen.

Ausgehend von der Formel für die Gewichtskraft des Körpers und den Auftriebskräften F_Ai:

$F_{G}=V_K \cdot \rho_K \cdot g$,

$F_{Ai}=V_K \cdot \rho_i \cdot g$

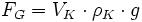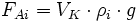
messen die beiden Waagen für die in die Flüssigkeit (oder das Gas) 1 oder 2 eingetauchten Massen die Gewichtskräfte

$\,F_{Gi}=F_G-|F_{Ai}|$

Eliminiert man aus den beiden Gleichungen für i = 1,2 das Volumen V_K, erhält man nach einigen einfachen mathematischen Umformungen die Lösung:

$\ \rho_K = \frac{F_{G1} \cdot \rho_2 - F_{G2} \cdot \rho_1}{F_{G1}-F_{G2}}$

Falls die eine Dichte sehr viel kleiner als die andere ist, 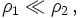$\ \rho_1 \ll \rho_2\,,$ etwa bei Luft und Wasser, vereinfacht sich die Formel zu:

$\ \rho_K = \frac{F_{G1} }{F_{G1}-F_{G2}}\cdot \rho_2$

Falls man nur eine Flüssigkeit, beispielsweise Wasser mit Dichte ρ_W, hat, kann man die obige Methode folgendermaßen anwenden:

Gewicht des Körpers vor Eintauchen:

$F_{G}=V_K \cdot \rho_K \cdot g$,

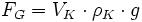Gewicht (reduziert) des Körpers nach (vollständigem) Eintauchen, wobei das Volumen V_K verdrängt wird (dies wird entweder durch den Überlauf aus dem vollen Gefäß, oder im Messzylinder gemessen):

$F_{Gr}=V_K \cdot \rho_K \cdot g - F_{A} = V_K \cdot g (\rho_K -\rho_W)$,

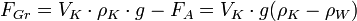also nach Umformen

$\rho_K = \rho_W + \frac {F_{Gr}} {V_k \cdot g}$

Nach dieser Methode bestimmte schon Archimedes die Dichte der Krone eines Königs, der zweifelte, ob diese wirklich aus reinem Gold bestehe (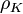$\,\rho_K$ = 19320 kg/m³.)

Auf der Auftriebmessung zur Dichtebestimmung von Flüssigkeiten beruhen das Aräometer und die Mohrsche Waage.

Weitere Messmethoden

• Pyknometer, Dichtebestimmung von Festkörpern durch Messen der verdrängten Flüssigkeitsvolumina.
• Isotopenmethode, Dichtebestimmung durch Strahlungsabsorption.
• Biegeschwinger, Dichtebestimmung durch Schwingungsmessung.

Abgrenzung zu anderen Begriffen

• Die Dichte darf nicht mit dem spezifischen Gewicht (Wichte) verwechselt werden. Während bei der Dichte die Masse im Verhältnis zum Volumen steht, steht beim spezifischen Gewicht an Stelle der Masse die Gewichtskraft.
• Die relative Dichte ist das Verhältnis der Dichte zur Dichte eines Normals, also eine dimensionslose Größe.

Definiert werden diese Unterschiede in der DIN 1306 Dichte; Begriffe, Angaben.

Spezielle Dichtebegriffe in der Technik

• Reindichte ρ₀, absolute Dichte, wahre Dichte, Skelettdichte (Volumen ohne Hohlräume)
• Rohdichte ρ, geometrische Dichte, scheinbare Dichte (eines porösen Körpers, Hohlräume inklusive)
  • Darrdichte, Raumdichte von Holz, Trockendichte der Gesteine (Materialkunde),
• Schüttdichte ρ_Sch eines Gemenges mit einem Fluid inklusive Luft
  • Korndichte, Hektolitergewicht (Logistik)
• Potentielle Dichte σ_θ (Ozeanographie)
• Dichten kompressibler Materialien: Pressdichte, Klopfdichte, Fülldichte, Stopfdichte, Raumdichte von Asphalt
• Sinterdichte von Sinterwerkstoffen

siehe auch: Gesteinsdichte, speziell zu Petrologie und Mineralogie

Als dimensionslose Vergleichsgröße:

• Relative Dichte d, spezifische Dichte
• Lagerungsdichte bindiger und nicht bindiger Böden (Bodenmechanik)

Andere Dichtebegriffe

Größen pro Raumeinheit

• Teilchendichte
• Raumladungsdichte
• Volumenleistungsdichte
• Volumetrische Energiedichte

Größen pro Flächeneinheit

(Empfohlene Bezeichnung nach DIN 5485: -flächendichte oder -bedeckung)

• Massenbelegung / „Flächengewicht“
• Oberflächenladungsdichte
• Stromdichte
• Strahlungsstromdichte
• Elektrische und Magnetische Flussdichte
• Flächenleistungsdichte
• Außerhalb Physik und Technik zum Beispiel Bevölkerungsdichte

Größen pro Längeneinheit

(Empfohlene Bezeichnung nach DIN 5485: -längendichte, -belag oder -behang)

• Linienladungsdichte

Mathematik

• Wahrscheinlichkeitsdichte

Tabellenwerte

Tabellenwerte zur Dichte verschiedener Stoffe sind in folgenden Artikeln zu finden:

Literatur

• DIN 1306 Dichte; Begriffe, Angaben

Weblinks

• Zur Dichte: Begriffe, Methoden und Verfahren
• Mineralienatlas – Dichte
• Dichte einiger Stoffe
• Versuche und Aufgaben zur Dichte