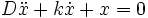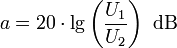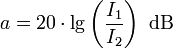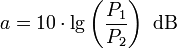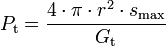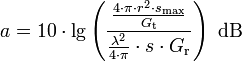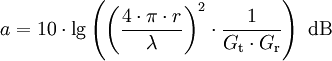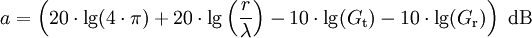Streckendämpfung

Als Dämpfung bezeichnet man in der Physik die Umwandlung von Schwingungsenergie in eine andere Energieform. Dies äußert sich beispielsweise in einem Abklingen eines Signals, einer Schwingung oder einer Welle. Eine Schwingung in einem gedämpften System verebbt, wenn ihr keine neue Energie zugeführt wird. Ein gedämpftes System verringert seine Amplitude, seine Intensität, seinen Ausschlag oder besser die Auslenkung seiner Schwingung oder Welle.

Allgemeine Beschreibung

Um die Dämpfung mathematisch zu beschreiben, wird ein Dämpfungsterm zur Gleichung eines Oszillators hinzugefügt.

Die Gleichung 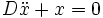$D \ddot x + x = 0$ beschreibt den ungedämpften harmonischen Oszillator, dessen Lösung harmonische Funktionen, wie Sinus und Kosinus sind. Die Dämpfung wird im einfachsten Fall als geschwindigkeitsabhängige Größe 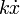$k \dot x$ eingefügt. Für den harmonischen Oszillator ergibt sich jetzt:

$D \ddot x + k \dot x + x = 0$

Darin heißt k Dämpfungskonstante.

Einen Ansatz, der wie hier proportional zur Geschwindigkeit ist, nennt man viskose Dämpfung.

Zu der Lösung des ungedämpften Oszillators kommt ein Dämpfungsterm der Form 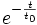$e^{-\frac{t}{t_0}}$ mit t₀ als Dämpfungskonstante.

Der Grad der Dämpfung steht im Zusammenhang mit der Abstimmschärfe eines Systems. Scharf abgestimmte Systeme haben eine geringe Dämpfung, sie brauchen lange, ehe sie in eine Resonanzschwingung geraten, klingen aber lange nach. Stark gedämpfte Systeme antworten schneller auf Resonanz, klingen aber kaum nach.

Die gedämpfte Schwingung kann eine elektrische Schwingung sein, die über ein Kabel oder als Funksignal übertragen wird, eine mechanische Schwingung oder eine optische Schwingung.

In der Regel wird die Dämpfung als positiver Wert angegeben. Das liegt am Verhältnis U₁/U₂. In der Audiotechnik und der Tontechnik ist nur die Verstärkung positiv und die Dämpfung negativ. Man geht dann vom Verhältnis U₂/U₁ aus.

Disziplinen

Mechanik

Beispiele für gedämpfte Schwingungen in der Mechanik sind:

• Saiteninstrumente, deren Holzkörper durch die Saiten angeregt werden und nachklingen.
• Dämpfung von Schwingungen im Fahrwerk von Fahrzeugen, etwa durch einen Stoßdämpfer im PKW.

Eigendämpfung

Dabei wird unterschieden zwischen Konstruktionen bzw. Bauteilen, die gezielt und ausschließlich die Dämpfung bewirken, Dämpfern - und solchen, die durch ihre Eigendämpfung neben der sonstigen Funktion auch eine schwingungsdämpfende Wirkung aufweisen.

Dazu gehören etwa Reifen, deren Karkasse durch Gewebe und Gummimischungen auf eine gewünschte Eigendämpfung abgestimmt wird. Auch in der Architektur bzw. Baustatik spielt die Eigendämpfung von Werkstoffen eine Rolle, um etwa ein durch Wind oder wechselnde Lasten bewirktes Schwingungsverhalten zu beeinflussen.

Elektrotechnik und Nachrichtentechnik

Alle Übertragungswege der Nachrichtentechnik sind gedämpfte Übertragungswege. Dieses gilt für optische ebenso wie für elektrische Übertragungswege. Durch die Dämpfung ist die ohne Verstärkung erreichbare Reichweite begrenzt.

In der Elektrotechnik und Akustik wird die Dämpfung a meistens in Dezibel dB angegeben. Sie berechnet sich üblicherweise aus der Eingangsspannung U₁ und der Ausgangsspannung U₂:

$a = 20 \cdot \lg \left( \frac{U_1}{U_2}\right)~\mathrm{dB}$

Analog dazu die Berechnung der Dämpfung mit Hilfe der Stromstärken:

$a = 20 \cdot \lg \left(\frac{I_1}{I_2}\right)~\mathrm{dB}$

Die Dämpfung kann auch mit Hilfe der Leistungen berechnet werden, da P~U². Sie berechnet sich aus der Eingangsleistung P₁ und der Ausgangsleistung P₂:

$a = 10 \cdot \lg \left(\frac{P_1}{P_2}\right)~\mathrm{dB}$

Wenn die Spannung auf den Wert von 50 % absinkt, also die halbe Spannung verloren geht, dann hat das Kabel (die Leitung) eine Dämpfung von 6,02 dB.

Wenn die Spannung auf den Wert von 70,7 % absinkt, ist die Dämpfung 3,01 dB.

Eine Dämpfung von 3 dB bedeutet, dass die Hälfte der eingespeisten Leistung nicht am Ausgang erscheint, sondern z. B. in Wärme umgewandelt wird.

Das bedeutet dass bei 3 dB Dämpfung die Spannung und der Strom auf 70,7 % abgesunken sind. Die Kontrolle kann einfach mit der Leistungsformel P = U·I durch das Einsetzen der Koeffizienten erfolgen: 0,5·P = 0,707·U·0,707·I

Dämpfung elektromagnetischer Wellen

Die Artikel Pfadverlust und Dämpfung überschneiden sich thematisch. Hilf mit, die Artikel besser voneinander abzugrenzen oder zu vereinigen. Beteilige dich dazu an der Diskussion über diese Überschneidungen. Bitte entferne diesen Baustein erst nach vollständiger Abarbeitung der Redundanz. mik81diss 15:47, 16. Jan. 2008 (CET)

Streckendämpfung

Die Streckendämpfung gibt bei ungestörter Ausbreitung die Dämpfung des gesendeten Signals über die Sendestrecke mit dem Radius r an.

$a = 10 \cdot \lg \left(\frac{P_\mathrm{t}}{P_\mathrm{rv}}\right)~\mathrm{dB}$

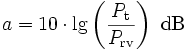
P_t = Sendeleistung

P_rv = Verfügbare Leistung am Empfängereingang

mit

$P_\mathrm{t} = \frac{4\cdot \pi \cdot r^2 \cdot s_\mathrm{max}}{G_\mathrm{t}}$

und

$P_\mathrm{rv} = \frac{\lambda^2}{4\cdot \pi} \cdot s \cdot G_\mathrm{r}$

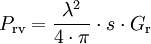
G = Gewinn der Antenne

s = Flächenleistungsdichte

ergibt sich:

$a = 10 \cdot \lg \left(\frac{\frac{4\cdot \pi \cdot r^2 \cdot s_\mathrm{max}}{G_\mathrm{t}}}{\frac{\lambda^2}{4\cdot \pi} \cdot s \cdot G_\mathrm{r}}\right)~\mathrm{dB}$

$a = 10 \cdot \lg \left(\left(\frac{4\cdot \pi \cdot r}{\lambda}\right)^2 \cdot \frac{1}{G_\mathrm{t} \cdot G_\mathrm{r}}\right)~\mathrm{dB}$

$a = \left(20 \cdot \lg (4\cdot \pi) + 20 \cdot \lg \left(\frac{r}{\lambda}\right) -10 \cdot \lg(G_\mathrm{t}) -10 \cdot \lg (G_\mathrm{r})\right)~\mathrm{dB}$

Der erste Faktor innerhalb der Logarithmusfunktion heißt auch Freiraumdämpfung.

Dämpfung durch Atmosphäre

Atmosphärische Dämpfung elektromagnetischer Strahlung

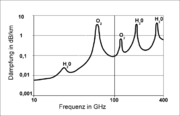
Elektromagnetische Wellen werden in der Atmosphäre gedämpft. Die Dämpfung nimmt mit der Frequenz zu, siehe Bild. Insbesondere Wasser in der Atmosphäre ist dafür verantwortlich, dass Frequenzen im K-Band in regenreichen Gebieten kaum für die Signalübermittlung genutzt werden. Die Absorptionslinien von Sauerstoff und Wasser liegen bei:

• 22,235 GHz (H₂O), 60 GHz (O₂), 118,75 GHz (O₂), 183,31 GHz (H₂O), 325,153 GHz (H₂O)

Literatur

• Dieter Meschede: Gerthsen Physik. 23. Auflage, Springer-Verlag, Berlin Heidelberg New York, 2006, ISBN 978-3-540-25421-8
• Jürgen Detlefsen, Uwe Siart: Grundlagen der Hochfrequenztechnik. 2. Auflage, Oldenbourg Verlag, München Wien, 2006, ISBN 3-486-57866-9
• Herbert Zwaraber: Praktischer Aufbau und Prüfung von Antennenanlagen. 9. Auflage, Dr. Alfred Hüthing Verlag , Heidelberg, 1989, ISBN 3-7785-1807-0
• Gregor Häberle, Heinz Häberle, Thomas Kleiber: Fachkunde Radio-, Fernseh-, und Funkelektronik. 3. Auflage, Verlag Europa Lehrmittel, Haan-Gruiten, 1996, ISBN 3-8085-3263-7

Siehe auch

• Gedämpfte Schwingung
• Dämpfungsfaktor
• Dämpfungsglied
• Schirmdämpfung
• Dämpfung der Sichtweite durch Atmosphäre
• Signaldämpfung bei DSL

Weblinks

• Berechnung des Dämpfungsfaktors und der Anpassungsdämpfung