Subset-Sum

Die Untermengensumme (engl. Subset Sum) ist ein berühmtes Problem der Informatik und des Operations Research. Es ist ein spezielles Rucksackproblem.

Problembeschreibung

Gegeben sei eine Menge von ganzen Zahlen I = {w₁,w₂,...,w_n}. Gesucht ist eine Untermenge, deren Elementsumme maximal, aber nicht größer als eine gegebene obere Schranke c ist (oft ist auch gefragt, die Schranke c exakt zu erreichen).

Formal: 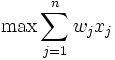$\operatorname{max} \sum_{j=1}^n {w_j x_j}$ so dass 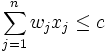$\sum_{j=1}^n {w_j x_j} \le c$ mit $x_j \in \{0,1\}.$

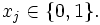
NP-Vollständigkeit

Das Problem ist NP-vollständig und somit vermutlich nicht effizient lösbar. Es kann mit der Branch-and-Bound-Methode gelöst werden.

Der Beweis der NP-Schwere erfolgt durch eine Reduktion von 3-SAT. Für eine gegebene Klauselmenge 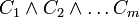$C_1 \wedge C_2 \wedge \ldots C_m$ mit den Variablen 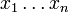$x_1 \ldots x_n$ werden die Zahlen 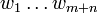$w_1 \ldots w_{m+n}$ sowie die Schranke c anhand einer Tabelle konstruiert. Es wird vorausgesetzt, dass keine Klauseln vorhanden sind, die x_i und 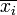$\overline{x_i}$ gleichzeitig enthalten; dies ist keine Einschränkung, da eine solche Klausel immer erfüllt wäre und somit weggelassen werden kann, ohne den Sinn zu verändern.

Beispielsweise wird die Formel 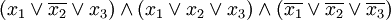$(x_1 \vee \overline{x_2} \vee x_3) \wedge (x_1 \vee x_2 \vee x_3) \wedge (\overline{x_1} \vee \overline{x_2} \vee \overline{x_3})$ wie folgt verarbeitet.

• Die ersten n Zeilen sind lediglich eine Codierung der Formel selbst: w₁ = 100110 besagt, dass x₁ in den Klauseln C₁ und C₂, aber nicht C₃ vorkommt. w₂ setzt das für 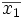$\overline{x_1}$ um, w₃ für x₂, w₃ für 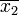$\overline{x_2}$ etc.
• Die Zeilen w_{n + 1} bis w_{n + m} sind "Korrekturzeilen", die nur auf der Diagonalen jeweils abwechselnd den Wert 1 oder 2 haben.
• Die Zahl c besteht nur aus n Einsen und m Vieren. Dies bewirkt, dass bei Addition der Spaltenwerte, an den ersten n Stellen nur entweder w₁ oder w₂; w₃ oder w₄ etc. ausgewählt werden kann, wodurch in der Formel x_i auf true oder false gesetzt wird. Die Vieren sind so gewählt, dass zusätzlich zu den beiden Korrekturwerten, die zusammen nur 1+2=3 ergeben, noch mindestens eine der Variablen in den Klauseln vorhanden sein muss, um auf 4 zu kommen. Sind mehr Variablen verfügbar, können entsprechend Korrekturzeilen weggelassen werden.

	x1	x2	x3	C1	C2	C3
w1	1	0	0	1	1	0
w2	1	0	0	0	0	1
w3	0	1	0	0	1	0
w4	0	1	0	1	0	1
w5	0	0	1	1	1	0
w6 = n	0	0	1	0	0	1
w7	0	0	0	1	0	0
w8	0	0	0	2	0	0
w9	0	0	0	0	1	0
w10	0	0	0	0	2	0
w11	0	0	0	0	0	1
w12 = n + m	0	0	0	0	0	2
c	1	1	1	4	4	4

Besitzt nun die boolesche Formel eine erfüllende Belegung, so nehmen wir falls x_i=true die Zahl w_{2i − 1} auf; falls x_i=false die Zahl w_2i. Damit sind schon die Einsen in c korrekt. Da eine erfüllende Belegung existiert, ist in den gerade hinzugefügten Zahlen in jeder Klausel mindestens eine erfüllte Variable vorhanden, somit tritt zu den möglichen Korrekturvariablen 1+2 noch jeweils mindestens eine 1 von der weiter oben erfüllten Variable, so dass in jedem Fall mindestens die gewünschte 4 erreicht wird. Sollten mehrere Variablen in einer Klausel erfüllt sein, so werden nach Bedarf Korrekturzahlen weggelassen. Mit der konstruierten Menge ist es so möglich, genau c zu erreichen, wenn die Formel erfüllbar ist.

Wenn nun c genau erreicht werden kann, so muss die Teilmenge der w_i zunächst jeweils genau ein w₁ oder w₂; w₃ oder w₄ etc. enthalten, weil sonst die Einsen in c nicht erfüllt wären. Somit ist gewährleistet, dass eine Variable tatsächlich true oder false (und nicht keins oder beides) ist. Durch diese Auswahl der Teilmenge muss dann auch jede Klausel erfüllt sein, denn wenn in einer Klausel keine Variable durch die Belegung erfüllt wäre, so würde die Addition nicht die notwendige Vier in c ergeben. Daher ist die boolesche Formel insgesamt erfüllbar.

Literatur

• Soma, Nei Y. Toth, Paolo: An exact algorithm for the subset sum problem. European Journal of Operational Research 136 S. 57-66
• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, und Clifford Stein. Algorithmen - Eine Einführung. Oldenbourg-Verlag, 2004. ISBN 3-486-27515-1. Seiten 1017ff.