Summerfield-Kriterium

Vulcain-2-Triebwerk einer Ariane 5

Strömungsabriß in einer Düse

Das Summerfield-Kriterium macht eine Aussage über die maximal zulässige Expansion einer Düse.

Grundlegendes

Will man eine Strömung auf Überschallgeschwindigkeit bringen, so muss man sie über eine Düse expandieren. Für eine Überschallströmung ist dieses nur möglich, indem man den Querschnitt stetig erweitert. Dieses beobachtet man zum Beispiel bei Düsen von Raketen wie dem hier abgebildeten Vulcain-2-Triebwerk. Ausgehend von einem engsten Querschnitt dem sogenannten kritischen Querschnitt wo die Strömungsgeschwindigkeit Ma = 1 beträgt wird der Querschnitt der Düse nun über die Bedingung $\frac{dA}{A} = (Ma ^2 -1) \frac{dw}{w}$ erweitert.

Hierbei sind $\frac{dA}{A}$ die Querschnittsänderung $\frac{dw}{w}$ die Geschwindigkeitsänderung und Ma die Machzahl.

Da die Formel nicht einfach zu verstehen ist, sollten wir sie genauer betrachten. Nehmen wir an, dass wir eine Strömung mit Ma < 1 betrachten. Nun wird der Term in der Klammer in jedem Fall negativ. Wollen wir nun eine Erhöhung der Geschwindigkeit also ein positives dw/w, so müssen wir dA/A negativ setzen also den Querschnitt verkleinern. Das heißt also: Um eine Strömung im Unterschall zu beschleunigen, müssen wir den Querschnitt verkleinern.

Betrachten wir nun den Fall im Überschall. Nun ist der Term in der Klammer auf jeden Fall positiv da Ma > 1 ist. Wollen wir nun ein positives dw/w also eine beschleunigte Strömung, so müssen wir den Querschnitt erweitern, da wir als Ergebnis auch ein positives dA/A herausbekommen. Daraus folgt, dass unser Querschnitt immer größer werden muss, wenn wir eine Überschallströmung betrachten. Genau dieses Prinzip sehen wir wieder auf dem Bild des Vulcain-II-Triebwerks, das in Strömungsrichtung vom kleinsten Querschnitt nach der Brennkammer wieder sukzessive größer wird.

Das Summerfield-Kriterium

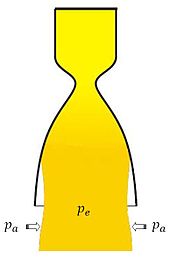
Nach dem Summerfield-Kriterium tritt Strömungsablösung an einer Düse bei einem Druckverhältnis von

${p_\mathrm{e} \over p_\mathrm{a}}$ ≈ 0,25 bis 0,4 auf.

Hierbei sind p_e der Druck am Düsenaustritt (exit) und p_a der Umgebungsdruck (ambient) der Düse.

Anschaulich lässt sich das Phänomen so erklären, dass bei der Beschleunigung des Fluids in der Düse der Druck immer weiter abfällt. Fällt der Druck unter den gegebenen Wert des Summerfield-Kriteriums, so „drückt“ der höhere Umgebungsdruck den Düsenstrahl soweit ein, dass dieser von der Düsenwand ablöst. Dieses tritt meistens sofort beim Start ein, da der Umgebungsdruck da am höchsten ist.

Beispiel

Sagen wir, wir befinden uns auf Meereshöhe und der Umgebungsdruck p_a beträgt 1 bar. Nach dem Summerfield-Kriterium können wir aus dem Druckverhältnis von 0,25 einen minimalen Druck am Düsenquerschnitt von 0,25 bar berechnen. Aus den Isentropenbeziehungen lassen sich nun bei gegebenem Brennkammerdruck p₀ die Machzahl am Austrittsquerschnitt und der gesamte Austrittszustand berechnen.

Konsequenzen

Löst die Strömung über der Düse ab, so geschieht dies an nicht vorhersehbaren Stellen aufgrund minimaler Druckschwankungen. Die Ablösung erfolgt jedoch in jedem Fall asymmetrisch und somit entstehen Momente infolge unterschiedlich starker Impulsströme über den Düsenaustritt. Diese Momente können das Triebwerk beschädigen und im schlimmsten Fall zum Verlust des Trägersystems führen.