Swapsort

Swap-Sort ist ein Sortieralgorithmus, der ein Array aus paarweise verschiedenen Zahlen sortiert.

Idee

Die Idee von Swap-Sort ist, von jedem Element eines Arrays A(1..n) die Anzahl m der kleineren Werte (die in A sind) zu zählen und das Element dann mit dem Element in A(m+1) zu vertauschen. Somit ist sichergestellt, dass das ausgetauschte Element bereits an der richtigen, also endgültigen Stelle steht.

Nachteil dieses Algorithmus ist, dass jedes Element nur einmal vorkommen darf, da sonst keine Terminierung erfolgt.

Prinzip

A ist ein Array mit n Elementen. Swap-Sort arbeitet in folgenden Schritten:

• (1) Beginne mit i=1
• (2) Zähle, wie viele Elemente kleiner als A(i) sind. Ist m diese Anzahl, so tausche A(i) mit A(m+1)
• (3) Ist i=m+1, so erhöhe i um 1
• (4) Ist i=n, so ist die Sortierung beendet - andernfalls gehe wieder zu Schritt 2

Beispiel

Es soll ein Array mit dem Inhalt [7|8|5|2|4|9|3|1] sortiert werden.

7 8 5 2 4 9 3 1   Mit dem Index 1 wird begonnen
^            
9 8 5 2 4 7 3 1   7 wurde mit A(5+1) getauscht
^         
1 8 5 2 4 7 3 9   9 wurde mit A(7+1) getauscht
^         
1 8 5 2 4 7 3 9   der Index wurde erhöht, da die Anzahl m der
  ^               kleineren Elemente von A(1) gleich dem Index-1 war         
1 3 5 2 4 7 8 9   8 wurde mit A(6+1) getauscht
  ^         
1 5 3 2 4 7 8 9
  ^         
1 4 3 2 5 7 8 9   der Index wurde erhöht, da die Anzahl m der
  ^               kleineren Elemente von A(2) gleich dem Index-1 war
1 2 3 4 5 7 8 9   ...usw.
    ^         
1 2 3 4 5 7 8 9
      ^         
1 2 3 4 5 7 8 9
        ^         
1 2 3 4 5 7 8 9
          ^         
1 2 3 4 5 7 8 9
            ^         
1 2 3 4 5 7 8 9  Das Array wurde komplett durchlaufen,
              ^  das Sortieren ist somit beendet

Implementierung

Ada

procedure swapsort (a: in out vector) is
 
z:integer;
 
	function ziel_pos(z:integer) return natural is
		anz:natural:=0;
	begin
		for i in a'range loop
			if a(i) <= z then
				anz:=anz+1;
			end if;
		end loop;
		return anz;
	end
 
begin
	for index in a'range loop
		z:=ziel_pos(a(index));
		while z /= index loop
			< vertausche a(index) mit a(z) >;
			z:=ziel_pos(a(index));
		end loop;
	end loop;
end;

Haskell

swapSort:: Ord a => [a] -> [a]
-- Vergleichsoperation wählbar
swapSort x = swapSort' x 0 (<)
	where
 	swapSort' x i r = if (i == (length x))
                        then x 
                        else let smaller = countSmaller x (x!!i) r
                             in if (i == smaller) then swapSort' x (i+1) r
                                                  else swapSort' (swap x i smaller) i r
	countSmaller [] _ _     = 0
	countSmaller (x:xs) y r = if (r x y) then 1+countSmaller xs y r else countSmaller xs y r
	swap x i1 i2 = let e1 = x!!i1
	                   e2 = x!!i2
		           in insert (remove (insert (remove x i1) e1 (i2-1)) i2) e2 i1
	remove (x:xs) 0 = xs
        remove (x:xs) n = x:remove xs (n-1)
        insert x y 0 = y:x
        insert (x:xs) y n = x:insert xs y (n-1)

Java

public class SwapSorter {
 
    public void sort(int[] sortMe) {
 
        int startwert = 0;
 
 
 
 
        while (startwert < sortMe.length - 1) {
 
            int kleinere = countSmallerOnes(sortMe, startwert);
 
            if (kleinere > 0) {
		int tmp = sortMe[startwert];
                sortMe[startwert] = sortMe[startwert + kleinere];
                sortMe[startwert + kleinere] = tmp;                
            }
            else
            {
                startwert++;
            }
        }
    }
 
    private int countSmallerOnes(final int[] countHere, final int index) {
        int counter = 0;
        for (int i = index + 1; i < countHere.length; i++) {
            if (countHere[index] > countHere[i]) {
                counter++;
            }
        }
        return counter;
    }
 
    // Testmain
    public static void main(String[] args) {
 
        int[] a = {3, 7, 45, 1, 33, 5, 2, 9};
        System.out.print("unsorted: ");
        for (int i = 0; i < a.length; i++) {
            System.out.print(a[i] + "  ");
        }
        System.out.println();
        new SwapSorter().sort(a);
        System.out.print("sorted: ");
        for (int i = 0; i < a.length; i++) {
            System.out.print(a[i] + "  ");
        }
    }
}

Python

def swap_sort(sortme):
    index = 0
    while index < len(sortme) - 1:
        new_index = sum(1 for x in sortme if x < sortme[index])
        if index == new_index:
            index += 1
        else:
            sortme[index], sortme[new_index] = sortme[new_index], sortme[index]
    return sortme

Komplexität

Die Komplexität von Swap-Sort kann mittels Landau-Symbol durch 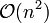$\mathcal{O}(n^2)$ ausgedrückt werden.

Siehe auch

• Liste von Algorithmen