- Symmetriepunktgruppe
-
Eine Punktgruppe ist ein spezieller Typus einer Symmetriegruppe der euklidischen Geometrie, der die Symmetrie einer Punktmenge (beispielsweise eines Körpers) beschreibt. Die Punktgruppe einer Symmetriegruppe enthält die so genannten Ableitungen der affinen Elemente einer Symmetriegruppe.
In der Kristallographie stellt jede der 32 möglichen Kristallklassen eine Punktgruppe dar. Deren Bestimmung ist somit ein wichtiger Schritt auf dem Weg zur Bestimmung der Raumgruppe, die die Symmetrie eines Kristalls beschreibt.
In der Molekülphysik sind Punktgruppen unentbehrlich, um aus spektroskopischen Daten auf die Symmetrie eines Moleküls zu schließen, oder um anhand der bekannten Symmetrie physikalische Eigenschaften vorherzusagen.
Inhaltsverzeichnis
Mathematische Grundlagen
Die Symmetriegruppe eines Körpers wird mathematisch als Menge aller möglichen Symmetrieoperationen beschrieben. Mit Symmetrieoperationen sind dabei euklidische Bewegungen gemeint, die den Körper auf sich abbilden. Zu unterscheiden sind dabei gerade Bewegungen, welche die Orientierung erhalten und ungerade, welche die Orientierung umkehren, z. B. Spiegelungen an Ebenen.
Mögliche Symmetrieoperationen in Punktgruppen im dreidimensionalen, euklidischen Vektorraum sind die Identitätsabbildung, Punktspiegelung an einem Inversionszentrum, Spiegelung an einer Spiegelebene, Drehung um eine Drehachse, sowie als Kombination daraus eine Drehspiegelung. Wenn man das Hintereinanderausführen von Symmetrieoperationen als additive Verknüpfung auffasst, erkennt man, dass eine Menge von Symmetrieoperationen eine (in der Regel nicht kommutative) Gruppe ist. Die Elemente einer Punktgruppe sind die Bilder der Symmetriegruppe unter dem Ableitungs-Homomorphismus. Diese Abbildung ist nicht injektiv, da beispielsweise sowohl Translationen als auch die Identitätsabbildung auf ihre linearen Teile abgebildet werden, welche in beiden Fällen die Identität der Punktgruppe darstellt. Punktgruppen enthalten mindestens einen Punkt, der Fixpunkt aller Symmetrieoperationen ist. Dies ist genau dann der Fall, wenn die Symmetriegruppe keine Translationen enthält, also immer bei beschränkten Körpern.
Internationale Nomenklatur
Es finden zwei Symbolsysteme breite Anwendung: In der Kristallographie hat sich das von Carl Hermann und Charles-Victor Mauguin abgeleitete System durchgesetzt, das die Zähligkeit der Symmetrie in den Vordergrund setzt. In der Molekülphysik ist die Symbolik von Schoenflies weit verbreitet, die auf den zugrundeliegenden Symmetrieelementen beruht.
System von Hermann-Mauguin
Zähligkeit der Achse: im Kristall nur 1, 2, 3, 4 oder 6, sonst auch 5, 7, ... Drehinversionsachse: - (über der Zahl) Symmetrieebene: m Kombination Drehachse/Ebene: /
Dabei wird in der internationalen Form nicht für alle Achsen eine Angabe gemacht, sondern verkürzt dargestellt. Z.B. mmm statt 2/m 2/m 2/m
System von Schoenflies
Drehgruppen: C Drehspiegelgruppen: S Diedergruppen: D Tetraedergruppen: T Oktaedergruppen: O Ikosaedergruppen: I Kugelgruppen: K
horizontale Symmetrieebene: h vertikale Symmetrieebene: v diagonale Symmetrieebene: d Inversionszentrum: i Spiegelebene: s
Dabei wird dem Gruppensymbol je nach Bedarf die Zähligkeit der Achse und/oder ein Symbol für andere Symmetrieelemente als Index angehängt, z.B. D2h
Kristallographische Bedeutung / Kristallklassen
Nicht alle Symmetrien eines Moleküls sind mit der Symmetrie eines Kristalls vereinbar: Wie Pierre Curie erkannte, sind in einem Kristall nur 6-, 4-, 3-, 2-zählige Drehachsen möglich (Drehungen um 60, 90, 120 bzw. 180 und jeweils Vielfache davon). Die Angabe einer 1-zähligen Drehachse bedeutet, dass ein Körper keine Drehsymmetrie besitzt. Eine 5-, 7- oder höherzählige Drehachse gibt es in Kristallen nicht, weil damit keine vollständige Raumausfüllung möglich wäre. Dennoch wurde eine 5-zählige Symmetrie in manchen metallischen Gläsern gefunden.
Es gibt im endlichdimensionalen Raum nur endlich viele mit Kristallsymmetrie verträgliche Punktgruppen. Speziell im dreidimensionalen euklidischen Raum gibt es 32 davon.
Die möglichen Symmetrien eines Kristalls werden mit den 230 kristallographischen Raumgruppen beschrieben. Können die Rotationsteile der Symmetrieoperationen zweier Raumgruppen bei beliebiger Basenwahl zur Übereinstimmung gebracht werden, so werden sie derselben geometrischen Kristallklasse, entsprechend einer der 32 kristallographischen Punktgruppen, zugeordnet. Fordert man, dass es sich dabei um eine primitive Basis handelt, so erhält man 73 arithmetische Kristallklassen, die den geometrischen Kristallklassen entsprechen, aber zusätzlich Gitterzentrierung besitzen. So entsprechen z.B. der geometrischen Kristallklasse 2 die arithmetischen Kristallklassen P2 und C2.
Weil das Beugungsbild von Kristallen in der Röntgenbeugung bei Abwesenheit anomaler Streuung immer ein Inversionszentrum enthält, werden Kristalle einer von 11 zentrosymmetrischen kristallographischen Punktgruppen zugeordnet, die auch als Lauegruppen bezeichnet werden.
Wichtige Punktgruppen (Tabellen)
Punktgruppen und Kristallklassen
Kristallsystem Kristallklasse Schönflies Hermann-Mauguin Hermann/Mauguin Kurzsymbol Triklin triklin-pedial C1 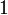
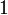
triklin-pinakoidal Ci 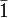
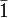
Monoklin monoklin-sphenoidisch C2 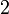
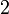
monoklin-domatisch Cs 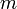
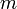
monoklin-prismatisch C2h 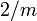
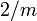
Orthorhombisch rhombisch-disphenoidisch D2 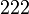
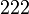
rhombisch-pyramidal C2v 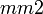
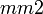
rhombisch-dipyramidal D2h 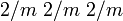
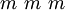
Tetragonal tetragonal-pyramidal C4 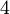
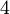
tetragonal-disphenoidisch S4 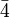
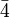
tetragonal-dipyramidal C4h 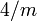
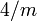
tetragonal-trapezoedrisch D4 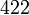
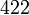
ditetragonal-pyramidal C4v 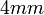
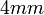
tetragonal-skalenoedrisch D2d 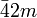 oder
oder 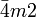
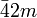
ditetragonal-dipyramidal D4h 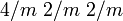
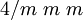
Trigonal trigonal-pyramidal C3 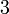
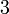
rhomboedrisch C3i 

trigonal-trapezoedrisch D3 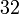 oder
oder 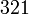 oder
oder 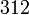
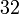
ditrigonal-pyramidal C3v 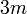 oder
oder 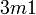 oder
oder 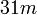
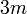
ditrigonal-skalenoedrisch D3d 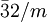 oder
oder 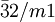 oder
oder 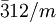
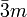
Hexagonal hexagonal-pyramidal C6 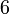
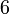
trigonal-dipyramidal C3h 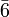
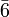
hexagonal-dipyramidal C6h 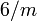
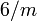
hexagonal-trapezoedrisch D6 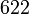
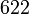
dihexagonal-pyramidal C6v 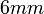
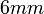
ditrigonal-dipyramidal D3h 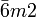 oder
oder 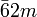
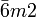
dihexagonal-dipyramidal D6h 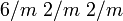
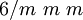
Kubisch tetraedrischpentagondodekaedrisch T 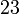
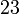
disdodekaedrisch Th 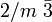
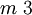
pentagonikositetraedrisch O 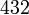
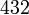
hexakistetraedrisch Td 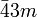
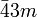
hexakisoktaedrisch Oh 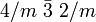
Punktgruppen und Molekülsymmetrie
Schönflies H. / M. Symmetrieelemente Molekülbeispiele Punktgruppen geringer Symmetrie C1 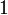
C1 CHFClBr Cs ≡ S1 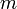
σ ≡ S1 BFClBr, SOCl2 Ci ≡ S2 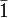
i ≡ S2 1,2-Dibrom-1,2-Dichlorethan, meso-Weinsäure ebene Drehgruppen SO(2) C2 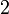
C2 H2O2, S2Cl2 C3 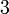
C3 Triphenylmethan, N(GeH3)3 C4 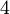
C4 12-Krone-4 C5 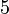
C5 15-Krone-5 C6 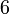
C6 18-Krone-6 Drehgruppen mit vertikalen Spiegelebenen C2v ≡ D1h 
C2, 2σv H2O, SO2Cl2, o-/m-Dichlorbenzol C3v 
C3, 3σv NH3, CHCl3, CH3Cl, POCl3 C4v 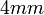
C4, 4σv SF5Cl, XeOF4 C5v - C5, 5σv Corannulen, C5H5In C6v 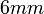
C6, 6σv Benzol-hexamethylbenzol-chrom(0) C∞v - C∞, ∞σv lineare Moleküle wie HCN, COS Drehgruppen mit horizontalen Spiegelebenen C2h ≡ D1d ≡ S2v 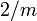
C2, σh, i Oxalsäure C3h ≡ S3 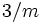
C3, σh Borsäure C4h 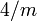
C4, σh, i Polycycloalkan C12H20 C6h 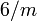
C6, σh, i Hexa-2-propenyl-benzol Drehspiegelgruppen S4 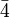
S4 Tetraphenylmethan, Si(OCH3)4 S6 ≡ C3i 
S6 Hexacyclopropylethan Diedergruppen D2 ≡ S1v 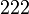
3C2 Twistan D3 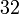
C3, 3C2 Tris-chelatkomplexe D4 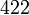
C4, 4C2 - D6 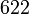
C6, 6C2 Hexaphenylbenzol Diedergruppen mit horizontalen Spiegelebenen D2h 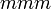
S2, 3C2, 2σv, σh, i Ethen, p-Dichlorbenzol D3h 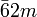
S3, C3, 3C2, 3σv, σh BF3, PCl5 D4h 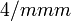
S2, C4, 4C2, 4σv, σh, i Re2(CO)10 D5h - S2, C5, 5C2, 5σv, σh IF7 D6h 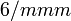
S2, C6, 6C2, 6σv, σh, i Benzol D∞h - S2, C∞, ∞σv lineare Moleküle wie Kohlendioxid, Ethin Diedergruppen mit diagonalen Spiegelebenen D2d ≡ S4v 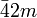
S4, 3C2, 2σd Propadien, Cyclooctatetraen, B2Cl4 D3d ≡ S6v 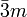
S6, C3, 3C2, 3σd, i Cyclohexan D4d ≡ S8v - S8, C4, 4C2, 4σd Cyclo-Schwefel (S8) D5d ≡ S10v - S10, C5, 5C2, 5σd Ferrocen Tetraedergruppen T 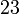
3S4, 4C3, 3C2 Pt(PF3)4 Th 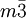
4S6, 4C3, 3C2, 3σh, i Fe(C6H5)6 Td 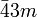
3S4, 4C3, 3C2, 6σd Methan, Phosphor (P4), Adamantan Oktaedergruppen O 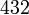
3C4, 4C3, 6C2 - Oh 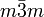
4S6, 3S4, 3C4, 4C3, 6C2, 3σh, 6σd, i SF6, Cuban Ikosaedergruppen I - 12S10, 10S6, 6C5, 10C3, 15C2 Fulleren-C20 (Pentagondodekaeder) Ih - 12S10, 10S6, 6C5, 10C3, 15C2, 15σv, i Fulleren-C60 räumliche Drehgruppen SO(3) Kh - ∞C∞, ∞σ, i einatomige Teilchen wie Helium, Elementarteilchen
Wikimedia Foundation.
