Symmetrieoperation

Wirken Transformationen invertierbar auf Objekte, beispielsweise Drehungen oder Spiegelungen auf die Punkte in einer Ebene, dann sind sie eine Symmetrie jedes Objekts, das sie dabei unverändert lassen. Beispielsweise sind Drehungen Symmetrien von Kreisen um den Drehpunkt.

Bei Drehungen und Spiegelungen eines Körpers heißt solche eine Transformation, die ihn auf sich abbildet, auch Symmetrieoperation des Körpers. Die Menge der Punkte, die von einer Symmetrietransformation unverändert gelassen werden, wird das zugehörige Symmetrieelement genannt. Zur Spiegelung an einer Ebene gehört die Spiegelebene als Symmetrieelement, zu einer Drehung um eine Achse die Drehachse.

Die Transformationen können kontinuierlich sein wie beispielsweise Verschiebungen um beliebige Strecken oder Drehungen um beliebige Winkel, aber auch diskret wie zum Beispiel eine Spiegelung oder Verschiebungen um ganzzahlige Vielfache von Gitterabständen oder Drehungen um Vielfache des rechten Winkels.

Eine Symmetrie der Bewegungsgleichungen eines physikalischen Systems liegt vor, wenn alle Lösungen der Bewegungsgleichungen wieder auf Lösungen abgebildet werden. Sind beispielsweise die Bewegungsgleichungen invariant unter Spiegelungen, dann ist jeder gespiegelte Ablauf genauso möglich wie das Urbild.

Ist in der Chemie der Hamilton-Operator eines Moleküls invariant unter einer Gruppe von Symmetrieoperationen, und wendet man die Symmetrieoperationen auf den Grundzustand an, so entstehen stabile Zustände gleicher Energie. Stimmen sie mit dem ursprünglichen Zustand überein, so ist er invariant und die Transformationen sind Symmetrien des Grundzustandes. Sind die transformierten Zustände vom ursprünglichen Grundzustand verschieden, so nennt man die Symmetrie spontan gebrochen. Beispielsweise ist die rechtsdrehende Milchsäure das Spiegelbild der gleich stabilen linksdrehenden Milchsäure. Dass im menschlichen Körper rechtsdrehende Milchsäure entsteht, bricht die Symmetrie zwischen rechts und links spontan ohne Grund.

Kontinuierliche Symmetrien

Folgen die physikalischen Gleichungen aus einem Prinzip der stationären Wirkung, so gehört zu jeder kontinuierlichen Symmetrie dieser Wirkung nach dem Noether-Theorem eine Erhaltungsgröße und umgekehrt gehört zu jeder nichttrivialen Erhaltungsgröße eine kontinuierliche Symmetrie der Wirkung. (Eine Erhaltungsgröße ist nichttrivial, wenn sie von den Größen wie Ort und Geschwindigkeit abhängt, die man anfänglich mit unterschiedlichen Werten vorgeben kann.)

Die wichtigsten kontinuierlichen Symmetrien der Physik sind:

• Homogenität der Zeit: Das Ergebnis eines Experiments hängt nicht davon ab, wann es durchgeführt wird,

Genauer: die Lagrangefunktion 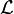$\mathcal L$ hängt nicht von der Zeit ab,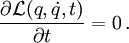 $\frac{\partial \mathcal{L}(q,\dot{q},t)}{\partial t}=0\,.$

Die zugehörige Erhaltungsgröße ist die Energie.

• Homogenität des Raumes: Das Ergebnis eines Experiments hängt nicht davon ab, wo es durchgeführt wird

Genauer: die Lagrangefunktion 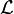$\mathcal L$ hängt nicht vom Ort ab,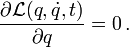 $\frac{\partial \mathcal{L}(q,\dot{q},t)}{\partial q}=0\,.$

Die zugehörige Erhaltungsgröße ist der Impuls.

• Isotropie des Raumes: Das Ergebnis eines Experiments hängt nicht von der Wahl der räumlichen Richtungen ab. Die zugehörige Erhaltungsgröße ist der Drehimpuls.
• Relativitätsprinzip: Das Ergebnis eines Experiments hängt nicht von der Geschwindigkeit des Inertialsystem ab, in dem es durchgeführt wird. Die zugehörige Erhaltungsgröße führt auf den Schwerpunktsatz.

Diskrete Symmetrien

Punktgruppe

Eine Symmetrieoperation eines Moleküls ist eine Kombination einer Drehung und gegebenenfalls Spiegelung, die das Molekül auf sich abbildet. Da die Symmetrieoperationen invertiert und hintereinander ausgeführt werden können, bilden sie eine Gruppe, die Punktgruppe des Moleküls.

Die Punktgruppe enthält die Identität E und kann zudem enthalten

• Spiegelung σ an einer Ebene
• Drehung um eine n-zählige Achse C_n (Drehung um 2π / n)
• Inversion i
• Drehspiegelung S_n Drehung um 2π / n mit Spiegelung an der zur Drehachse senkrechten Ebene

Die zugehörigen Symmetrieelemente sind

• Spiegelebene,
• Drehachse,
• Inversions-Punkt,
• Drehspiegelachse.

Andere wichtige, diskrete Symmetrien der Physik sind:

• Symmetrien eines Kristallgitters bilden seine Raumgruppe,
• Raumspiegelung P (Paritätstransformation): Spiegelung des Raumes an einem Punkt
• Zeitspiegelung T: Umkehr aller anfänglichen Geschwindigkeiten und Ströme
• Ladungskonjugation C: Austausch von Teilchen und Antiteilchen.

Symmetrieverletzungen

Die Thermodynamik ist nicht T-invariant, da es umgekehrte Wärmeströme von kalt zu heiß nicht gibt und die Zunahme der Entropie eine Zeitrichtung auszeichnet (siehe auch: Zeitpfeil).

Von den elementaren Wechselwirkungen sind die Gravitation, die elektromagnetischen und die starken Wechselwirkungen C-, P- und T-invariant. Die Schwache Wechselwirkung ist nicht invariant unter Raumspiegelung, wie 1956 im Wu-Experiment gezeigt. Das Verhalten von K-Mesonen und B-Mesonen ist auch nicht invariant unter der gleichzeitigen Spiegelung und Austauschung von Teilchen. Ohne diese CP-Verletzung wäre beim Urknall gleich viel Materie wie Antimaterie entstanden, die sich bis heute zerstrahlt hätte. Erst die CP-Verletzung erklärt die Baryonenasymmetrie, also das heutige Überwiegen von Materie.

Eichtransformationen

Die Parameter der bisher angegeben Transformationen, beispielsweise Drehwinkel, sind unabhängig vom Ort. Solche Transformationen nennt man globale Transformationen. Kann der Transformationsparameter, wie beispielsweise bei Verschiebung der Bestandteile eines Gummituchs, an jedem Ort (abgesehen von Stetigkeitsbedingungen) frei gewählt werden, spricht man von lokalen Transformationen oder von Eichtransformationen. Physikalische Theorien, deren Wirkung invariant unter Eichtransformationen sind, heißen Eichtheorien. Alle fundamentalen Wechselwirkungen, Gravitation, die elektromagnetische, schwache und starke Wechselwirkung werden nach heutigem Wissen durch Eichtheorien beschrieben.

Siehe auch

• Symmetrie
• Symmetrie (Geometrie)
• Gruppentheorie (Anwendung in der Chemie/Physik)
• Charaktertafel
• CPT-Theorem
• Symmetriebruch

Literatur

• Michel, Louis: Symmetry defects and broken symmetry. Configurations Hidden Symmetry. Rev. Mod. Phys., 1980, 52, 617–651

Weblinks

• Symmetry and Symmetry Breaking. Eintrag in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)Vorlage:SEP/Wartung/Parameter 1 und weder Parameter 2 noch Parameter 3