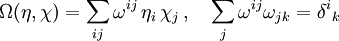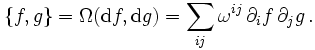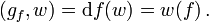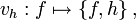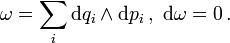Symplektische Topologie

In der Mathematik bezeichnet eine symplektische Mannigfaltigkeit eine glatte Mannigfaltigkeit M zusammen mit einer symplektischen Form ω, das heißt einer globalen glatten 2-Form, die punktweise nicht ausgeartet ist. Manchmal wird auch noch gefordert, dass die Form geschlossen ist, dass also dω = 0 gilt.

Poisson-Klammer

Da die Form 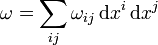$\omega=\sum_{ij}\omega_{ij}\,\mathrm dx^i\,\mathrm d x^j$ nicht ausgeartet ist, definiert sie mit ihrem Inversen an jedem Punkt eine bilineare Abbildung von Eins-Formen $\eta=\sum_i\eta_i\, \mathrm d x^i$ und $\chi=\sum_j\chi_j\, \mathrm d x^j$

$\Omega(\eta,\chi) =\sum_{ij} \omega^{ij}\,\eta_i\, \chi_j\,,\quad \sum_j \omega^{ij}\omega_{jk}=\delta^i{}_k$

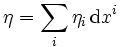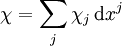
und die Poisson-Klammer der Funktionen f und $g\,,$

$\{f, g\}=\Omega(\mathrm d f, \mathrm d g) = \sum_{ij}\omega^{ij}\,\partial_i f\, \partial_j g\,.$

Hamiltonscher Fluss

In einem Euklidischen Raum ist der Gradient einer Funktion f dasjenige Vektorfeld g_f, dessen Skalarprodukt mit jedem Vektorfeld w mit dem Anwenden von df auf w übereinstimmt,

$(g_f,w) =\mathrm d f(w) = w(f)\,.$

In einer symplektischen Mannigfaltigkeit gehört zu jeder Funktion h das Vektorfeld

$v_h:f\mapsto \{f,h\}\,,$

das Funktionen f längs der Integralkurven der zu h gehörigen Hamiltonschen Gleichungen ableitet. Das Vektorfeld v_h ist der symplektische Gradient von h oder der infinitesimale Hamiltonsche Fluss von h.

Satz von Darboux

In der Umgebung jedes Punktes einer symplektischen Mannigfaltigkeit gibt es lokale Koordinaten q_i,p_i mit $\omega = \sum_{i} \mathrm d q_i \and \mathrm d p_i\$

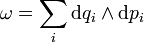
Ein Beweis findet sich im Buch von Arnold in Kapitel 8.

Zusammenhang zur Hamiltonschen Mechanik

In der Hamiltonschen Mechanik ist der Phasenraum eine symplektische Mannigfaltigkeit mit der geschlossenen, symplektischen Form

$\omega = \sum_{i} \mathrm d q_i \and \mathrm d p_i\,,\ \mathrm d \omega = 0\,.$

Dies ist kein Spezialfall, denn nach dem Satz von Darboux lässt sich ω in lokalen Koordinaten immer als 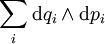$\sum_{i} \mathrm d q_i \and \mathrm d p_i\$ schreiben. Bei symplektischen Mannigfaltigkeiten handelt es sich um die Phasenräume Hamiltonscher Mechanik.

Literatur

• Arnold, V. I. Mathematical Methods of Classical Mechanics, Springer-Verlag (1989), ISBN 0-387-96890-3

Siehe auch

• Kanonische Transformation