- Systemeigenschaft
-
Unter den Systemeigenschaften versteht man einen Satz von Eigenschaften, die für ein System charakteristisch sind. Sie ergeben sich einerseits aus den Eigenschaften der Elemente des Systems und andererseits aus der Systemstruktur, also ihren Beziehungen untereinander.
Inhaltsverzeichnis
Komplexität
Sie ist gekennzeichnet durch die Art und Zahl der Elemente sowie Art, Stärke, Zahl und Dichte der Wechselbeziehungen auf der Mikroebene.
Die Komplexität bzw. Kompliziertheit wird durch die Anzahl der Elemente und Beziehungen bestimmt. Man unterscheidet zwischen struktureller Komplexität (Quotient aus Anzahl der Relationen und Elemente; Komplexitätsmaß = K =nr / ne ) und Zeitlicher Komplexität. Das heißt die Anzahl der möglichen Zustände, die das System in einer Zeitspanne annehmen kann.
Beschreibung der Extrema:
einfache Systeme komplexe Systeme Anzahl der Elemente gering groß Ähnlichkeit der Elemente in allen Merkmalen gleich in allen Merkmalen verschieden Menge der Beziehungen gering groß Dichte der Beziehungen (Vernetzungsgrad) gering groß Beispiel: Pendel Chloroplast Zwischen einfachen und komplexen Systemen sind alle Ausprägungsgrade der Extrema möglich.
Die Komplexität eines Systems hängt von der Definition der Systemgrenzen, von der Zahl der als relevant erachteten Elemente und von den als relevant betrachteten Wechselbeziehungen ab. Viele komplexe Systeme weisen eine hierarchieähnliche Gliederung auf: Je näher (zeitlich und/oder räumlich) man herantritt, um so mehr Details werden sichtbar. Dabei können unabhängig vom Maßstab immer wieder dieselben Strukturen auftreten. In diesem Fall liegt keine Hierarchie sondern Selbstähnlichkeit vor. Selbstähnlichkeit ist in der Biologie weniger bei Strukturen (siehe aber Blumenkohl) als bei Grundprinzipien zu finden, z. B. gelten die Regeln der Evolution (Überproduktion – Variation – Selektion) auf allen Struktur- und Zeitebenen.
Dynamik
Sie ist gekennzeichnet durch das zeitliche Verhalten des Systems. Statische Systeme zeigen ohne Einflüsse von außen sowohl auf der Makroebene als auch auf der Mikroebene keine Veränderungen (Beispiel: ruhendes Pendel). Dynamische Systeme sind auf der Mikroebene dauernden Veränderungen unterworfen, können aber zumindest zeitweise auf der Makroebene einen stationären Zustand einnehmen (Beispiele: chemische Gleichgewichtsreaktion, Ökosystem Wald). Ob ein System als statisch oder dynamisch betrachtet wird, hängt vom Zeitmaßstab und von der Zeitdauer der Beobachtung des Systems ab. Dies wird deutlich bei Systemen im Gleichgewicht, die aber um ihre Gleichgewichtslage schwanken: Ist der Beobachtungszeitraum zu kurz, kann nicht ermittelt werden, ob es sich um Schwankungen um einen Mittelwert handelt oder ob ein ansteigender oder absinkender Trend vorliegt (Beispiel: Klimaschwankungen seit Beginn der direkten Messungen). Wird ein sehr großer Maßstab gewählt, sind die Schwankungen gar nicht feststellbar, das System verhält sich scheinbar statisch.
Wechselwirkung
Systeme und Elemente sind durch Beziehungen miteinander verknüpft. Diese Beziehungen können Energie-, Stoff- und Informationsflüsse sein.
Möglichkeiten auf der Makroebene:
- Isolierte Systeme haben weder einen Stoff- noch einen Energieaustausch mit der Umwelt.
- (Ab)geschlossene Systeme können zwar Energie mit der Umwelt austauschen, nicht aber Stoffe.
- Offene Systeme tauschen mit der Umwelt sowohl Stoffe als auch Energie aus.
Je nach den definierten Systemgrenzen kann ein System als isoliert, abgeschlossen oder offen betrachtet werden, da hiervon die Unterscheidung zwischen System und Umwelt abhängt.
Isolierte und geschlossene Systeme kommen in der Realität praktisch nicht vor, ihre Modellierung ist aber bei der Untersuchung von sehr komplexen Systemen notwendig.
Determiniertheit
Die Determiniertheit ist der Grad der „Vorbestimmtheit“ des Systems: Ein System geht von einem Zustand Z1 in den Zustand Z2 über: Z1 → Z2. Bei deterministischen Systemen ist dieser Übergang bestimmt (zwingend), bei stochastischen wahrscheinlich.
Deterministische Systeme erlauben prinzipiell die Ableitung ihres Verhaltens aus einem vorherigen Zustand, stochastische Systeme nicht. Klassische deterministische Systeme erlauben eine eindeutige Bestimmung ihres Zustandes zu jedem Zeitpunkt der Vergangenheit und Zukunft mit hinreichender Genauigkeit (Beispiel: Planetenbewegung). Hinreichend ist hier bezogen auf menschlich überschaubare, bzw. relevante Zeiträume und Größenordnungen. Die Entwicklung chaotischer Systeme ist nicht immer eindeutig bestimmbar, da alle Parameter mit theoretisch unendlich großer Genauigkeit bekannt sein müssen, sie sind empfindlich gegenüber den Anfangsbedingungen. Mit entsprechenden (mathematischen) Modellen lassen sich relevante Aussagen über Vergangenheit und Zukunft von deterministischen und stochastischen Systemen machen. Aus der Komplexität eines Systems lässt sich keine Aussage über die Vorhersagbarkeit treffen: Es gibt einfache deterministische Systeme, die chaotisch sind (z. B. Doppelpendel) und komplexe deterministische Systeme (Chloroplasten bei der Photosynthese).
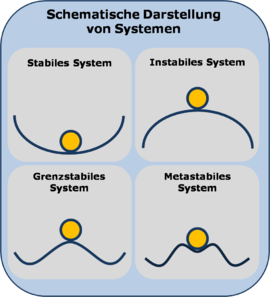
Stabilität
Betrachtungen der Reaktion eines Systems auf der Makroebene im stationären Zustand auf Störungen von außen
Möglichkeiten stabil metastabil instabil, labil grenzstabil, indifferent Reaktion kehrt in den ursprünglichen Zustand zurück kehrt in den ursprünglichen zurück oder geht in einen neuen stabilen Zustand über kehrt nicht mehr in den ursprünglichen (labilen) Zustand jede Störung führt zu einem neuen (stabilen) Zustand Beispiel chemisches System Systeme mit minimaler Enthalpie und maximaler Entropie Ein Wasserstoff-Sauerstoffgemische ist stabil, bis es aktiviert wird, dann reagiert es zu Wasser aktivierter Übergangszustand Verdünnen von Schwefelsäure Beispiel Balkenpendel Schwerpunkt liegt unterhalb des Drehpunktes Schwerpunkt liegt oberhalb des Drehpunktes Schwerpunkt und Drehpunkte fallen zusammen Betrachtung der Elemente auf der Mikroebene
Bei stabilen Systemen ändert sich die Struktur des Systems nicht. Zahl, Art und Wechselwirkung der Elemente bleibt konstant. Bei instabilen Systemen genügen geringe Änderungen der Systembedingungen, um eine Änderung der Struktur herbei zu führen. Diese können sowohl von außen, als auch durch innere Eigendynamik hervorgerufen werden.
Mit zunehmender Komplexität geht die Austauschbarkeit der Elemente und damit die strukturelle Stabilität verloren. Wird bei hochkomplexen Systemen ein Element gegen ein anderes ausgetauscht, das nicht mehr dieselben Eigenschaften hat, kann sich das Gesamtverhalten des Systems verändern. (Beispiel: Organtransplantation).
Welche Stabilität eines Systems festgestellt wird, hängt vom festgelegten Zeitmaßstab und dem Beobachtungszeitraum ab sowie von der Definition der Störung: Manche stabilen Systeme gehen bei genügend starken Störungen in instabile Zustände über (Beispiel: Aktivierung chemischer Reaktionen). Alle Systeme können bei starken Störungen zerstört werden.
Abhängigkeit der Zuordnung von Systemgrenzen
Die Zuordnung zu einer der Stabilitätskategorien hängt auch von der Definition der Systemgrenzen ab:
Beispiel System Kugel / Schüssel:
Bei Störung, d. h. Anstoßen der Kugel, rollt die Kugel wieder in ihre Ausgangslage zurück. Ein zu starker Stoß befördert die Kugel aus der Schüssel heraus, die Kugel fällt zu Boden. Damit ist das ursprüngliche System zerstört. Wird aber das System Kugel/Schüssel/Boden betrachtet, ist die Kugel in der Schüssel nur in einem metastabilen Zustand, da sie am Boden einen stabileren Zustand einnimmt.
Liegt die Kugel auf einer umgekehrten Schüssel (labiles System), führt jede Störung auch zur Zerstörung. Wird aber das System umgekehrte Schüssel/Kugel/Boden betrachtet, führt jede Störung zu einem neuen Zustand.
Beispiel Balkenpendel
Hier kann das System je nach dem Lageverhältnis Schwerpunkt zu Drehpunkt drei verschiedene Zustände einnehmen, die sich gegenüber Störungen unterschiedlich verhalten: exzentrische Anordnung: Es gibt genau einen stabilen Zustand, alle anderen Zustände sind instabil. Für ein anders Pendelsystem mit zentrischer Lagerung (Drehpunkt und Schwerpunkt fallen zusammen) gibt es unendlich viele Möglichkeiten der Ausrichtung des Balkens, die aber alle instabil sind.
Zeitvarianz
Zeitvarianz beschreibt die Abhängigkeit des Systemverhaltens vom Zeitpunkt der Betrachtung. Ein zeitvariantes System verhält sich zu verschiedenen Zeitpunkten unterschiedlich. Bei technischen Systemen liegt der Grund dafür meist in zeitabhängigen Parameterwerten, bei biologischen Systemen beispielsweise in unterschiedlichen Umweltbedingungen. Zeitinvariante Systeme dagegen verhalten sich zu jeder Zeit gleich. Eine mechanische Uhr ist zum Beispiel zeitinvariant, wenn man Verschleiß vernachlässigt. Ein Pendel, bei dem die Länge der Aufhängung sich mit der Zeit ändert, ist zeitvariant.
weitere Eigenschaften
- diskret (zeit- oder zustandsdiskret) – kontinuierlich
- linear - nichtlinear
- zweck- oder zielorientiert
- adaptiv (anpassend)
- autonom (unabhängig von äußerer Steuerung)
- autopoietisch (selbstfortpflanzend)
- denkend
- lernend
- steuernd
- regelnd, selbstregulierend
- trivial - nichttrivial
- verteilt/konzentriert parametrisch
Wikimedia Foundation.