Takagi-Sugeno-Regler

Der Takagi-Sugeno-Regler ist ein auf der Fuzzy-Logik beruhender Regler. Sein Verhalten wird mit Regeln durch unscharfes Schließen beschrieben. Im Schlussfolgerungsteil der Regeln stehen im Gegensatz zu relationalen Fuzzy-Reglern nach Mamdani keine unscharfen Mengen sondern Funktionen der Eingangsgrößen. Die Funktionswerte werden mit den Erfüllungsgraden der Regeln gewichtet. Das Ergebnis ist die scharfe Stellgröße. Es ist also keine Defuzzyfizierung notwendig.

Grundlagen

Zugehörigkeitsfunktionen

In der Fuzzy-Logik werden linguistischen Variablen umgangssprachliche Begriffe als Wertebereich zugeordnet. Zum Beispiel kann die linguistische Variable Regelabweichung die Werte negativ_klein, nahe_null oder positiv_klein annehmen. Mathematische Repräsentation dieser Begriffe ist die Zugehörigkeitsfunktion (Fuzzy-Menge). Sie beschreiben, mit welchem Wert zwischen 0 und 1 eine scharfe Größe zu dieser Fuzzy-Menge gehört. Die Fuzzy-Logik stellt auch Operatoren für die logischen Operationen UND und ODER bereit.

Das Verhalten eines Takagi-Sugeno-Reglers wird durch Regeln der Form

Ri : WENN x1 = A1l UND ... UND xn = Ank DANN yi = f(x1,...,xn)

beschrieben. Dabei sind

• x_j scharfe Eingangsgrößen.
• A_nk Wert einer linguistischen Variablen.
• y_i Funktionen der Eingangsgrößen x_j.

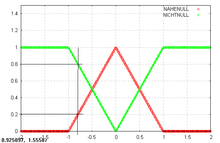
Beispiel: Ein nichtlineares System soll mit P-Reglern geregelt werden. $x\,$ ist die Regelabweichung.

R1 : WENN x = NAHENULL DANN $y_1=0.4\cdot x$
R2 : WENN x = NICHTNULL DANN $y_2=2.5\cdot x$

Fuzzyfizierung

Für jeden linguistischen Wert wird über dessen Zugehörigkeitsfunktion ein Zugehörigkeitsgrad der scharfen Eingangsgröße ermittelt. Die fuzzyfizierte Eingangsgröße ist ein Vektor der Zugehörigkeitsgrade. Sind μ_ij(x) die den linguistischen Werten A_ij entsprechenden Zugehörigkeitsfunktionen und x_i die scharfen Eingangsgrößen, dann gilt für die fuzzyfizierte Eingangsgröße $x_F\,$:

xF(xi) = (μi1(xi),...,μin(xi))

Im obigen Beispiel erhalten wir für x = − 0.8 für

R1 : xF(x) = 0.2
R2 : xF(x) = 0.8

Inferenz

Die Auswertung der Prämissen erfolgt oft mit dem Minimum-Operator (siehe T-Norm). Der Erfüllungsgrad α_i der Regel R_i ist demzufolge

αi = min(μi1(xi),...,μin(xi)).

Für unser Beispiel gilt

α1 = 0.2
α2 = 0.8

Konklusion

Im Schlussfolgerungsteil der Regel stehen keine linguistischen Werte. Deshalb ist keine Defuzzyfizierung notwendig. Die scharfe Ausgangsgröße ergibt sich als mit den Erfüllungsgraden der Regeln gewichteter Mittelwert der Stellgrößen zu

  $y=\frac {\sum_{i=1}^ny_i\cdot \alpha_i}{\sum_{i=1}^n\alpha_i}$

Für das Beispiel erhalten wir die Scharfe Stellgrösse

y =  − 1.664

Vergleich zu Mamdani

Wenn man einen Takagi-Sugeno-Regler 0. Ordnung beschreibt, das heißt einen, bei dem alle Funktionen konstante Funktionen sind, ist dieser Regler ein Sonderfall des Mamdani-Systems, bei dem alle Ausgangsgrößen Singletonvariablen sind.

Literatur

• Holger Lutz, Wolfgang Wendt: Taschenbuch der Regelungstechnik : mit MATLAB und Simulink, Verlag Harri Deutsch, 8. Auflage 2010, ISBN 978-3-8171-1859-5