- Fuzzylogik
-
Fuzzylogik (engl. fuzzy ‚verwischt‘, ‚verschwommen‘, ‚unbestimmt‘; fuzzy logic, fuzzy theory ‚unscharfe Logik‘ bzw. ‚unscharfe Theorie‘) ist eine Theorie, welche vor allem für die Modellierung von Unsicherheiten und Unschärfen von umgangssprachlichen Beschreibungen entwickelt wurde. Sie ist eine Verallgemeinerung der zweiwertigen Booleschen Logik. Beispielsweise kann damit die sogenannte Fuzziness von Angaben wie ein bisschen, ziemlich oder stark mathematisch in Modellen erfasst werden. Die Fuzzylogik basiert auf den Fuzzy-Mengen (Fuzzy-Sets) und sogenannten Zugehörigkeitsfunktionen, die Objekte auf Fuzzy-Mengen abbilden, sowie passenden logischen Operationen auf diesen Mengen und ihrer Inferenz. Bei technischen Anwendungen müssen außerdem Methoden zur Fuzzyfizierung und Defuzzyfizierung betrachtet werden, das heißt Methoden zur Umwandlung von Angaben und Zusammenhängen in Fuzzylogik und wieder zurück, zum Beispiel als Stellwert für eine Heizung als Resultat.
Inhaltsverzeichnis
Historische Entwicklung
Die Wurzeln einer Logik der Unschärfe reichen zurück in die griechische Antike. Bereits der Philosoph Platon postulierte, dass zwischen den Begriffen wahr und falsch ein dritter Bereich liege. Dies ganz im Gegensatz zu seinem Zeitgenossen Aristoteles, welcher die Präzision der Mathematik darin begründete, dass eine Aussage nur entweder wahr oder falsch sein kann.
Die Fuzzy-Set-Theorie, also die unscharfe Mengenlehre, wurde 1965[1] von Lotfi Zadeh, Professor der University of California, Berkeley, entwickelt. Die Fuzzy-Technologie nahm in den 1980er Jahren vor allem in Japan ihren Aufschwung mit der sogenannten japanischen Fuzzy-Welle. Ein historisches Beispiel ist die Regelung der vollautomatischen U-Bahn Sendai, die erste erfolgreiche Großanwendung mit Fuzzylogik in der Praxis. Später fand die Fuzzylogik auch in Geräten der Unterhaltungselektronik breite Anwendung. Die europäische Fuzzy-Welle kam erst Mitte der 1990er Jahre, als die Grundsatzdiskussionen über die Fuzzylogik verebbten.
Fuzzy-Set-Theorie
Die Fuzzy-Set-Theorie ist von der mehrwertigen Logik zu unterscheiden, die in den 1920er Jahren der polnische Logiker Jan Łukasiewicz beschrieb. Im engeren Sinne kann die so genannte Fuzzylogik zwar als eine mehrwertige Logik gedeutet werden, und insofern gibt es eine gewisse Nähe zur mehrwertigen Logik, für deren Wahrheitswert einer logischen Aussage Zahlen aus dem reellen Einheitsintervall [0, 1] (die reellen Zahlen von 0 bis 1) verwendet werden. Allerdings fasst Zadeh die Fuzzy-Set-Theorie als Formalisierung von unbestimmten Begriffsumfängen im Sinne einer referenziellen Semantik auf, was ihm erlaubt, die Unschärfe der Zugehörigkeit von Objekten als Elemente der zu definierenden Mengen graduell über numerische Werte zwischen 0 und 1 anzugeben. Damit eröffnete sich eine weitergehende, linguistische Interpretation der Fuzzy-Set-Theorie als Basis einer Logik der Unschärfe. Der Begriff der Fuzzy Logik wurde zunächst auch nicht von Zadeh, sondern erst später von dem ebenfalls in Berkeley tätigen Linguisten George Lakoff benutzt, nachdem Joseph Goguen, ein Doktorand Zadehs, eine Logik unscharfer Begriffe[2] eingeführt hatte. Siehe in diesem Zusammenhang den von Hegel geprägten Begriff der Gedoppelten Mitte.
Anwendungsbeispiele
Fuzzylogik wird heute in unterschiedlichen Bereichen eingesetzt: Anwendung findet sie in Bereichen der Automatisierungstechnik, Betriebswirtschaft, Medizintechnik, Unterhaltungselektronik, Fahrzeugtechnik, Regelungstechnik, künstlichen Intelligenz, Spracherkennung und anderen Bereichen. Nützlich ist die Verwendung von Fuzzylogik oft dann, wenn keine mathematische Beschreibung eines Sachverhaltes oder Problems vorliegt, sondern nur eine verbale Beschreibung. Auch wenn – wie fast immer – das vorhandene Wissen Lücken aufweist oder teilweise veraltet ist, bietet sich der Einsatz von Fuzzylogik an, um noch zu einer fundierten Aussage über einen aktuellen oder künftigen Systemzustand zu gelangen. Dann wird aus sprachlich formulierten Sätzen und Regeln mittels Fuzzylogik eine mathematische Beschreibung gewonnen, die in Rechnersystemen genutzt werden kann. Interessant ist dabei, dass mit der Fuzzylogik auch dann Systeme sinnvoll gesteuert (bzw. geregelt) werden können, wenn ein mathematischer Zusammenhang zwischen den Ein- und Ausgabegrößen eines Systems nicht darstellbar ist – oder nur mit großem Aufwand erfolgen könnte, so dass eine Automatisierung zu teuer oder nicht in Echtzeit realisierbar wäre.
Weitere Anwendungen sind die Regelung von U-Bahnen, die Prognose der zukünftigen Last in Routern, Gateways oder Mobilfunk-Basisstationen, die Steuerung automatischer Getriebe in Automobilen, Alarmsysteme für die Anästhesie, Zwischenfrequenzfilter in Radios, ABS für Automobile, Brandmeldetechnik, die Prognose des Energieverbrauchs bei Energieversorgern, AF-gekoppelte Mehrfeld-Belichtungsautomatiken und AF-Prädikation in Spiegelreflexkameras etc.
Auch in betriebswirtschaftlichen Anwendungen hat Fuzzylogik erfolgreich Einzug gehalten. Ein erfolgreiches Beispiel ist die Intelligente Schadenprüfung (ISP), mit der sich weltweit Versicherungsunternehmen vor Versicherungsbetrug schützen.
Unscharfe Mengen
Grundlage der Fuzzylogik sind die so genannten unscharfen Mengen (engl.: "fuzzy sets"). Im Gegensatz zu traditionellen Mengen (im Kontext der Fuzzylogik auch scharfe Mengen genannt), in denen ein Element einer vorgegebenen Grundmenge entweder enthalten oder nicht enthalten ist, kann ein Element in einer unscharfen Menge auch ein wenig enthalten sein. Der Grad an Zugehörigkeit wird dabei durch eine Zugehörigkeitsfunktion (membership function) µ beschrieben, die den Elementen einer Grundmenge eine reelle Zahl zwischen 0 und 1 zuordnet.
Auch auf unscharfen Mengen sind Operationen wie auf scharfen Mengen möglich, wie z. B. die Bildung von Schnittmengen (UND), Vereinigungsmengen (ODER) und Komplementmengen (NICHT). Zur Modellierung der logischen Operatoren der Konjunktion (UND), der Disjunktion (ODER) und der Negation (NICHT) bedient man sich der Funktionsklassen der T-Norm und T-Conorm.
Fuzzyfunktionen
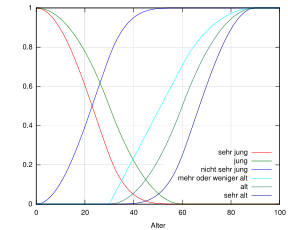
Zusammenfassungen einzelner Zugehörigkeitsfunktionen ergeben die Fuzzyfunktionen. Ein Beispiel dafür ist eine Fuzzyfunktion für das Alter eines Menschen. Diese könnte aus mehreren dachförmigen Dreiecken bestehen, die ihrerseits für verschiedene Alterstypen stehen und Zugehörigkeitsfunktionen dieser einzelnen Alterstypen darstellen. Jedes Dreieck deckt einen Bereich von mehreren Jahren des Menschenalters ab. Ein Mensch mit 45 Jahren hätte so die Eigenschaften: noch jung mit der Wertung 0,75 (das ist noch relativ viel), mittleres Alter mit der Wertung 0,25 (das ist ein bisschen) und von den übrigen Funktionen nichts. Anders ausgedrückt: mit 45 ist man ziemlich viel noch jung und ein bisschen mittel. Die Fuzzyfunktion ordnet jedem Alterswert eine ihn charakterisierende Zugehörigkeitsfunktion zu.
In vielen Fällen werden Fuzzyfunktionen über Tabellen aus statistischen Erhebungen erzeugt. Diese können auch von der Anwendung selbst erhoben werden soweit eine Rückkopplung gegeben ist, wie z. B. in der Fahrstuhlsteuerung. Praktisch bedeutsam ist auch, die Erfahrungen und Intuitionen eines Experten auf dem jeweiligen Gebiet in eine Fuzzyfunktion mit einfließen zu lassen, insbesondere dann, wenn überhaupt keine statistischen Aussagen vorhanden sind, beispielsweise dann, wenn es sich um ein komplett neu zu beschreibendes System handelt.
Diese Dreiecksgestalt ist allerdings keineswegs zwingend, generell können die Werte von Fuzzy-Funktionen beliebige Gestalt haben, solange deren Funktionswerte im Intervall [0,1] bleiben. In der Praxis werden solche Dreieckfunktionen aufgrund ihrer einfachen Berechenbarkeit jedoch gerne verwendet. Relativ weit verbreitet sind noch Trapeze (nicht notwendigerweise spiegelsymmetrisch), aber auch Halbkreise finden sich in einigen Anwendungen. Auch können sich prinzipiell mehr als zwei Abschnitte einer Fuzzy-Funktion überlappen (beim hier betrachteten Beispiel scheint das aber nicht sinnvoll zu sein).
Beispiel für eine nicht-lineare Fuzzy-Funktion
Ein Beispiel für eine nicht-lineare Zugehörigkeitsfunktion bildet die folgende Sigmoidfunktion:

Die Kurve drückt durch die Form des Buchstabens S eine ansteigende Zugehörigkeit zu der jeweils beschriebenen Menge durch einen Wert im Wertebereich [0,1] aus. Je nach Anwendungsfall lässt sich eine abnehmende Zugehörigkeit durch eine entsprechende Z-Kurve ausdrücken:
Z(x,a,δ) = 1 − S(x,a,δ)
Der Parameter a gibt hierbei den Wendepunkt der S-Kurve an, der Wert δ bestimmt die Neigung der Kurve. Je größer δ gewählt wird, desto flacher wird der Verlauf der resultierenden Funktion.
Das Alter eines Menschen lässt sich mittels dieser Kurve wie folgt als Fuzzy-Funktion darstellen:
Alter eines Menschen Bezeichnung Zugehörigkeitsfunktion sehr jung 
jung 
nicht mehr sehr jung 
mehr oder weniger alt 
alt 
sehr alt 
Dabei können die umgangssprachliche Modifikatoren sehr, mehr oder weniger sowie nicht mehr durch einfache Modifikation einer gegebenen Funktion dargestellt werden:
- Der umgangssprachlich verstärkende Modifikator sehr kann in Form eines erhöhten Exponenten dargestellt werden (im Beispiel
 ). Das Ergebnis ist ein steilerer Kurvenverlauf im Vergleich zur Ausgangsfunktion.
). Das Ergebnis ist ein steilerer Kurvenverlauf im Vergleich zur Ausgangsfunktion. - Der umgangssprachliche Modifikator mehr oder weniger kann durch Verwendung eines niedrigeren Exponenten bzw. der Quadratwurzel auf eine gegebene Funktion ausgedrückt werden(
 ). Das Ergebnis ist ein flacherer Kurvenverlauf im Vergleich zur Ausgangsfunktion.
). Das Ergebnis ist ein flacherer Kurvenverlauf im Vergleich zur Ausgangsfunktion. - Die Negation eines umgangssprachlichen Ausdrucks lässt durch eine einfache Subtraktion darstellen (s2 = 1 − s0).
Den Anwendungfällen entsprechend handelt es sich bei dieser Form der Repräsentation um linguistische Variablen. Letztlich wird aus den einzelnen gewichteten Aussagen ein einziger Zahlenwert berechnet, der das Alter in mathematischer Form auszudrücken vermag. Mit diesem Wert lässt sich dann präzise weiterarbeiten. Auch bei dieser so genannten Defuzzyfikation sind viele Verfahren möglich, das bekannteste (aber bei weitem nicht immer beste) ist sicherlich die Methode Center-of-Gravity, bei der der Zahlenwert gewichtet nach der Masse der geometrischen Form der einzelnen Abschnitte der Zugehörigkeitsfunktion gebildet wird. Eine andere Möglichkeit ist, einfach einen gewichteten Mittelwert der Funktionswerte zu bilden.
Begriffsabgrenzung
Nicht zu verwechseln mit der Fuzzylogik ist die Fuzzy-Suche, die eine unscharfe Suche in Datenbanken ermöglicht, zum Beispiel, wenn die genaue Schreibweise eines Namens oder Begriffes nicht bekannt ist.
Auch wenn die Zugehörigkeits-Werte aus dem Intervall [0,1] formal wie Wahrscheinlichkeitswerte aussehen, so ist Unschärfe etwas grundsätzlich anderes als Wahrscheinlichkeit.
Vor allem ist zu beachten, dass die Summe der Werte zweier Funktionen, die sich überschneiden, nicht 1 sein muss. Sie kann gleich 1 sein, aber auch darüber oder darunter liegen.
Literatur
- Benno Biewer: Fuzzy-Methoden. Praxisrelevante Rechenmodelle und Fuzzy-Programmiersprachen. Berlin [u.a.]: Springer, 1997. ISBN 3-540-61943-7
- Christoph Drösser: Fuzzy logic. Methodische Einführung in krauses Denken. Reinbek bei Hamburg: Rowohlt, 1996. ISBN 3-499-19619-0
- Siegfried Gottwald: Fuzzy Sets and Fuzzy Logic. Foundations of Application - from a Mathematical Point of View. Vieweg: Braunschweig/Wiesbaden und Teknea: Toulouse, 1993.
- Berthold Heinrich [Hrsg.:] Messen, Steuern, Regeln. Elemente der Automatisierungstechnik. 8. Aufl. Wiesbaden: Vieweg, 2005. ISBN 3-8348-0006-6
- Ulrich Höhle, Stephen Ernest Rodabaugh: Mathematics of Fuzzy Sets: Logic, Topology, and Measure Theory. Springer, 1999, ISBN 0-7923-8388-5.
- Michels, Klawonn, Kruse, Nürnberger: Fuzzy-Regelung. Grundlagen, Entwurf, Analyse. Springer-Verlag. ISBN 3-540-43548-4
- George J. Klir, Bo Yuan: Fuzzy Sets and Fuzzy Logic: Theory and Applications, 1995, ISBN 0-13-101171-5
- Thomas Kron: Fuzzy-Logik für die Soziologie. In: Österreichische Zeitschrift für Soziologie, 2005, H. 3: 51-89.
- Thomas Kron/Lars Winter: Fuzzy Systems - Überlegungen zur Vagheit sozialer Systeme. In: Soziale Systeme, 2005, H. 2: 370-394.
- Lars Winter/Thomas Kron: Fuzzy Thinking in Sociology. In: Seising, Rudi (Hrsg.): Views on Fuzzy Sets and Systems From Different Perspectives. Philosophy and Logic, Criticisms and Applications. Berlin, Heidelberg: Springer, 2009: 301-320.
- Andreas Mayer [u.a.]: Fuzzy Logic. Einführung und Leitfaden zur praktischen Anwendung. Bonn [u.a.]: Addison-Wesley, 1993. ISBN 3-89319-443-6
- Daniel McNeill u. Paul Freiberger: Fuzzy Logic. Die unscharfe Logik erobert die Technik. Droemer Knauer, München 1994 ISBN 3-426-26583-4
- Rodabaugh, S.E.; Klement, E.P (Eds.): Topological and Algebraic Structures in Fuzzy Sets: A Handbook of Recent Developments in the Mathematics of Fuzzy Sets. Springer, 2003, ISBN 978-1-4020-1515-1.
- Carsten Q. Schneider, Claudius Wagemann: Qualitative Comparative Analysis (QCA) und Fuzzy Sets. Verlag Barbara Budrich, 2007. ISBN 978-3-86649-068-0
- Rudolf Seising: Die Fuzzifizierung der Systeme. Die Entstehung der Fuzzy Set Theorie und ihrer ersten Anwendungen - Ihre Entwicklung bis in die 70er Jahre des 20. Jahrhunderts. Stuttgart: Franz Steiner Verlag (Boethius: Texte und Abhandlungen zur Geschichte der Mathematik und der Naturwissenschaften Band 54) 2005. ISBN 3-515-08768-0
- Hans-Jürgen Zimmermann: Fuzzy Set Theory and its Applications, 2001, ISBN 0-7923-7435-5
- Wolfgang Anthony Eiden: Präzise Unschärfe - Informationsmodellierung durch Fuzzy-Mengen. Ibidem Verlag, 2002. ISBN 3-89821-230-0, PDF
Einzelnachweis
- ↑ Zadeh, Lotfi A.: Fuzzy sets. Information and Control. 1965; 8: 338–353
- ↑ Goguen, J.A., "The logic of inexact concepts". Synthese 19(3/4):325–373, 1969
Siehe auch
- Verwandte Begriffe: Unschärfe und Ungewissheit
- Dreiwertige Logik
- Lineare partielle Information
Weblinks
 Commons: Fuzzylogik – Sammlung von Bildern, Videos und Audiodateien
Commons: Fuzzylogik – Sammlung von Bildern, Videos und Audiodateien- Eintrag, in: Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)
- Buch zum Thema (PDF; 1,27 MB)
- DAX-Fuzzy-Logik-Automat von Klaus Harnack
- Fuzzy Logik Image Processing (engl.)
- 7 Wahrheiten über Fuzzy Logik (engl.)
- Englische Einführung in das Thema (Fuzzy Logic Introduction, M. Hellmann, PDF; 260 kB)
- Ein Anwendungsbeispiel - Herzog, Christof; Das Methodenpaket IeMAX mit dem Fuzzy-Simulationsmodell FLUCS - Entwicklung und Anwendung eines Entscheidungsunterstützungssystems für die integrative Raumplanung http://e-diss.uni-kiel.de/diss_622/
- Fuzzy Logic Definition im Atrox.at Wiki
- Einführung in Fuzzy Logic (engl.)
- Einführung in Fuzzy Logic
- Dissertation about fuzzy logic in profitability analysis (engl.)
Software und Tools
- Der umgangssprachlich verstärkende Modifikator sehr kann in Form eines erhöhten Exponenten dargestellt werden (im Beispiel
Wikimedia Foundation.