- Torricellis Trompete
-
Gabriels Horn (auch Torricellis Trompete) ist ein von Evangelista Torricelli entdeckter Körper, der eine unendliche Oberfläche, aber ein endliches Volumen besitzt. Der Name leitet sich zum einen aus der einem Blasinstrument ähnelnden Form, zum anderen aus der Tradition her, den Erzengel Gabriel als den Engel anzusehen, der das Horn bläst, um das Jüngste Gericht anzukündigen, wobei dabei die Unendlichkeit mit der Göttlichkeit assoziiert wird.
Mathematische Definition
Gabriels Horn ergibt sich, wenn man den Graphen der Funktion
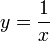 mit dem Definitionsbereich
mit dem Definitionsbereich 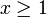 (um die Polstelle bei x = 0 zu vermeiden) um die x-Achse rotieren lässt. Volumen (V) und Fläche (A) dieses Rotationskörpers berechnen sich auf folgende Weise:
(um die Polstelle bei x = 0 zu vermeiden) um die x-Achse rotieren lässt. Volumen (V) und Fläche (A) dieses Rotationskörpers berechnen sich auf folgende Weise:Um das nachvollziehen zu können, muss man wissen, dass für alle
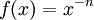 mit
mit 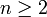 das uneigentliche Integral von 1 bis
das uneigentliche Integral von 1 bis  existiert, das heißt gegen einen endlichen Wert konvergiert:
existiert, das heißt gegen einen endlichen Wert konvergiert:Dahingegen ist die Fläche unter der Kurve
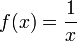 unbeschränkt, denn die Stammfunktion dieser Kurve ist der natürliche Logarithmus:
unbeschränkt, denn die Stammfunktion dieser Kurve ist der natürliche Logarithmus:Erläuterung des Paradoxons
Einerseits bräuchte man unendlich viel Farbe, um die Innen- oder Außenfläche des Horns vollständig zu bedecken, andererseits könnte man das Innere des Horns mit einer endlichen Menge Farbe füllen. Die Auflösung dieses scheinbaren Paradoxons besteht darin, dass zum Bestreichen der gesamten Innenfläche des Körpers eine Farbschicht mit unendlich kleiner Dicke nötig wäre, die kein Volumen hätte.
Weblinks
- Thomas Peters: Gabriels Horn
- Torricellis Trompete auf PlanetMath (engl.)
- Eric W. Weisstein: Gabriel's Horn auf MathWorld (englisch)
Wikimedia Foundation.



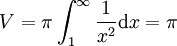
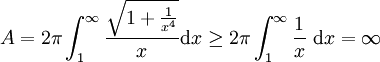
![\int_{1}^{\infty}x^{-n}\mathrm{d}x = \left[\frac{1}{1 - n} x^{1-n}\right]_{1}^{\infty} = \frac{1}{n - 1}](/pictures/dewiki/50/2a5df0623ffcb3c8381dcf34a800028f.png)
![\int_{1}^{\infty}\frac{1}{x}\mathrm{d}x = \left[\ln x \right]_{1}^{\infty} = \infty](/pictures/dewiki/98/b9fdcfb24495ec5695c70109c6b86f60.png)