Transfinite Rekursion

Transfinite Induktion ist eine Beweistechnik in der Mathematik, die die von den natürlichen Zahlen bekannte Induktion auf beliebige wohlgeordnete Mengen verallgemeinert, zum Beispiel auf Mengen von Ordinalzahlen oder Kardinalzahlen, oder sogar auf die echte Klasse aller Ordinalzahlen.

Sei A eine wohlgeordnete Menge (oder Klasse). Will man beweisen, dass die Eigenschaft P für alle Elemente von A zutrifft, so genügt es Folgendes zu beweisen:

• Ist 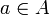$a \in A$ und ist P(b) wahr für alle 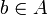$b \in A$ mit b < a, dann gilt auch P(a).

Dass dies ausreicht, sieht man wie folgt:

Sei 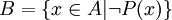$B = \{x \in A | \neg P(x)\}$ die Menge (bzw. Klasse) derjenigen Elemente x von A, für die P(x) nicht zutrifft. Träfe die Eigenschaft P nicht für alle Elemente von A zu, so wäre B nicht leer und enthielte aufgrund der Wohlordnung ein kleinstes Element a. Für jedes b mit b < a gilt dann 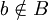$b \notin B$, also P(b). Nach dem Gezeigten folgt P(a).

Andererseits folgt aus 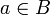$a \in B$ sofort 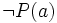$\neg P(a)$. Da sich somit ein Widerspruch ergibt, muss die Annahme, dass P nicht für alle Elemente von A zutrifft, falsch gewesen sein.

Wenn A die Klasse der Ordinalzahlen ist, zerlegt man den Beweis aus technischen Gründen häufig in folgende drei einzeln zu beweisende Fälle:

• P(0) ist wahr.
• Ist a eine Ordinalzahl, so folgt aus P(a) auch P(a + 1).
• Ist a eine Grenzzahl und gilt P(b) für jede Ordinalzahl b < a, so gilt auch P(a).

Transfinite Rekursion

Bei den natürlichen Zahlen ist es bekanntlich möglich, Funktionen rekursiv zu definieren, also auf eine dem Beweis durch vollständige Induktion analoge Methode (Beispiel: 0!: = 1 und $n!:=n \cdot (n-1)!$ für n > 0). Auf dieselbe Weise gehört zur transfiniten Induktion das Definitionsverfahren der transfiniten Rekursion:

Ist A wohlgeordnet und kann man f(a) durch die Werte f(b) ausschließlich an Stellen b < a definieren, so ist hierdurch bereits f auf ganz A definiert.

Formaler gilt: Führen wir die Bezeichnungen 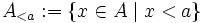$A_{&amp;lt;a}:=\{x\in A\mid x&amp;lt;a\}$ und $A_{\le a}:=\{x\in A\mid x \le a\}$ ein, so gilt der folgende

Rekursionssatz: Sei A eine wohlgeordnete Menge, B eine beliebige Menge.

Für alle 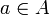$a \in A$ sei eine Abbildung 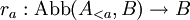$r_a: \mathrm{Abb}(A_{&amp;lt;a},B) \to B$ gegeben.

Dann existiert genau eine Abbildung 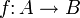$f\colon A \to B$ mit $f(a) = r_a( f \mid_{A_{&amp;lt;a}} )$ für alle $a \in A$.

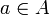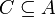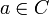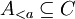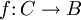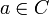Beweis: Unter einem Abschnitt von A wollen wir eine Teilmenge $C \subseteq A$ verstehen, bei der aus $a \in C$ stets auch $A_{&amp;lt;a} \subseteq C$ folgt. Ist C ein Abschnitt und $f\colon C\to B$ eine Abbildung, so sagen wir, dass f die Rekursion erfüllt, falls $f(a) = r_a( f \mid_{A_{&amp;lt;a}} )$ für alle $a\in C$ gilt. Offenbar ist A selbst ein Abschnitt und jeder andere Abschnitt C ist von der Form A _{< a}, nämlich für das kleinste Element a der nichtleeren Menge $A\setminus C$.

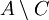Die Menge aller Abschnitte von A ist durch Inklusion wohlgeordnet. Ist nämlich S eine nichtleere Menge solcher Abschnitte, so gilt min(S) = A im Fall S = {A} und ansonsten ist offenbar A _{< m} mit 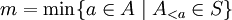$m=\min\{a\in A\mid A_{&amp;lt;a}\in S\}$ ein kleinstes Element.

Wir zeigen durch transfinite Induktion die folgende Aussage P(C) über Abschnitte C von A:

• Es gibt genau eine die Rekursion erfüllende Abbildung $f\colon C\to B$.

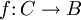Wir setzen also voraus, dass die Aussage für alle kleineren Abschnitte gilt, d.h. dass P(A _{< a}) für alle 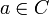$a\in C$ gilt. Die demnach eindeutig bestimmte die Rekursion erfüllende Abbildung 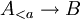$A_{&amp;lt;a}\to B$ heiße f_a.

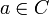Die Eindeutigkeit von f folgt leicht: Sind $f,g\colon C\to B$ zwei die Rekursion erfüllende Funktionen und ist $a\in C$ beliebig, so stimmen f und g nach Induktionsvoraussetzung auf dem kleineren Abschnitt A _{< a} miteinander sowie mit f_a überein und es folgt f(a) = r_a(f_a) = g(a).

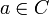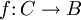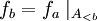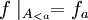Zur Existenz: Für beliebiges $a\in C$ setze man f(a): = r_a(f_a) und erhält so eine Abbildung $f\colon C\to B$. Ist b < a, so folgt aus der Eindeutigkeit $f_b=f_a\mid_{A_{&amp;lt;b}}$, also $f(b)=r_b(f_b)=r_b(f_a\mid_{A_{&amp;lt;b}})=f_a(b)$. Dies bedeutet $f\mid_{A_{&amp;lt;a}}=f_a$ und somit $f(a)=r_a(f\mid_{A_{&amp;lt;a}})$, d.h. f erfüllt die Rekursion.

Durch transfinite Induktion folgt also, dass P(C) für alle Abschnitte C gilt, insbesondere gilt P(A), aber das ist genau die zu beweisende Aussage des Rekursionssatzes.