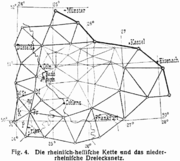
Triangulationsnetz

Vermessungsnetz

Die Triangulation (Aufteilen einer Fläche in Dreiecke) ist das klassische Verfahren zur Erstellung eines trigonometrischen Netzes als Dreiecksnetz für die Zwecke der Erdmessung, der Landesaufnahme sowie als Grundlage für weitere Vermessungsarbeiten.

Verwendet wird das Dreiecksnetz insbesondere als Netz erster Ordnung.

Dieser Artikel bezieht sich im Wesentlichen auf die Anwendung der Triangulation in der Kartographie bzw. Geodäsie und ihrer Geschichte.

Methodik

Vermessung eines Punkts im Dreieck

Verfahren der Triangulation in der Geodäsie

Winkel lassen sich im Gelände wesentlich einfacher (berührungslos) und genauer messen als Längen, besonders wenn die Längen sehr groß sind. Daher wurde für die großräumige Vermessung der Erdoberfläche das Verfahren der Triangulation verwendet. Sind die Winkel zwischen den Seiten eines Dreiecks und die Länge einer seiner Seiten bekannt, so lassen sich die Längen der anderen Seiten mittels trigonometrischer Formeln berechnen. Damit ergeben sich auch die Lagebeziehungen der Dreieckspunkte in einem Koordinatensystem.

Als Voraussetzung muss die Länge einer Seite eines Dreiecks bekannt sein. Da die Seiten mit einer Ausdehnung von 30–50 km jedoch zu lang für eine direkte Messung sind, wird eine kürzere Strecke von nur einigen Kilometern Länge zwischen zwei Festpunkten mit einem Basismessgerät durch Aneinanderlegen von Maßstäben oder mit Messbändern oder -drähten genauestens vermessen. Diese nennt man auch die Basis des Trigonometrischen Netzes. Die ermittelte Länge wird durch ein Basisvergrößerungsnetz auf eine Seite des eigentlichen Netzes übertragen, von der ausgehend alle restlichen Seiten berechnet werden können.

Spezielle moderne Triangulationsverfahren der Geodäsie sind:

• Stellartriangulation: In der Landesvermessung werden die Zielpunkte nicht mit direkter Winkelmessung, sondern durch fotografische Aufnahmen vor dem Hintergrund des Sternhimmels eingemessen
• Satellitentriangulation: In der Satellitengeodäsie ein Verfahren zur Einmessung von Bodenstationen mittels gleichzeitig fotografierter Satellitenpositionen

Erstellen eines Dreiecksnetzes

Historische Kleine Pyramide

Beschreibungsschild zur kleinen Pyramide

Durch Verbinden der Dreiecke mit gemeinsamen Eckpunkten zu einem Dreiecksnetz können die schon bestimmten Seiten eines Dreiecks als Basis zur Berechnung der benachbarten Dreiecke dienen.

Als Dreieckspunkte wurden geodätische Festpunkte auf erhöhten Stellen der Landschaft, beispielsweise Bergkuppen oder ersatzweise Türmen, errichtet. Hohe Bauwerke sind allgemein weniger geeignet, da sie sich senken und dabei ihre Neigung und damit die Lage des erhöhten Punktes verändern können. Von jedem dieser Punkte werden mit einem Theodolit die Winkel zwischen sämtlichen hier endenden Dreiecksseiten ermittelt, indem die jeweils anderen Punkte der Seite angezielt werden. Dazu müssen die Punkte untereinander freie Sicht haben.

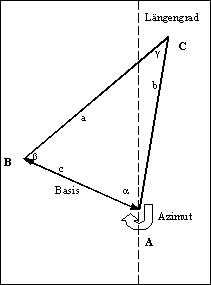
Damit sind aber erst die Lagebeziehungen der Punkte untereinander ermittelt. Das Netz ließe sich noch als Ganzes auf der Erdoberfläche verschieben und drehen. Daher wird noch ein Fundamentalpunkt ausgewählt. Mittels astronomischer Beobachtungen wird seine genaue Lage im geodätischen Gradnetz und die Nord-Abweichung der Richtung (Azimut) zu einem weiteren Festpunkt bestimmt.

In der Regel wird das Dreiecksnetz überbestimmt, das heißt, es werden nicht nur die Dreiecke bestimmt, die zu einer einfachen Überdeckung des Messgebietes notwendig sind, sondern alle, die sich durch die gegenseitige Beobachtbarkeit der Punkte ergeben. So kann durch Ausgleichsrechnung die Genauigkeit gesteigert werden.

Dreiecksnetz und Erdfigur

Um die trigonometrischen Formeln überhaupt anwenden zu können, muss die Berechnung auf einer mathematisch beschreibbaren Fläche durchgeführt werden, der Erdfigur. Zunächst verwendete man als erste Näherung eine Kugel, dann ein Rotationsellipsoid, dessen eine Achse mit der Rotationsachse der Erde zusammenfällt. Setzt man die Länge dieser Achsen in die Gleichungen ein, kann man wiederum durch Minimieren der auftretenden Fehler das bestangepasste Ellipsoid finden.

Die Parameter dieses Ellipsoids (Längen der Halbachsen bzw. Abplattung) zusammen mit den Parametern des Fundamentalpunkts (Lage und Ausrichtung) bezeichnet man als Geodätisches Datum.

Netz erster und zweiter Ordnung

Das so bestimmte Dreiecksnetz ist das Netz 1. Ordnung. Da seine Punkte sehr weit voneinander entfernt liegen, wird es wiederum durch Triangulation verdichtet zu einem Netz 2. Ordnung mit einem Punktabstand in der Größenordnung von 10 km, und dieses wiederum zu weiteren Netzen mit geländeabhängigen Punktabständen.

Diese Punkte kann man dann als Festpunkte für kleinräumige Vermessungen verwenden, und in diesem Größenrahmen auch mit den Formeln der ebenen Trigonometrie rechnen:

Gegeben sind: Gerade c, Winkel α und β

$\gamma = 180^{\circ} - \alpha - \beta, a = c \cdot \frac{\sin{\alpha}}{\sin{\gamma}}, b = c \cdot \frac{\sin{\beta}}{\sin{\gamma}}$

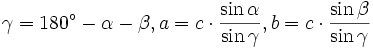
Geschichte der Triangulation in der Geodäsie

Triangulationspunkt im Vierungsturm des Kölner Doms. Hier verlief im 19. Jahrhundert der Nullmeridian für Deutschland.

Die Grundlagen der Trigonometrie gehen zurück auf die Antike. Hipparch von Nikaia (gest. 120 v. Chr.) und Menelaus von Alexandria (ca. 100 n. Chr.) definierten erste Zusammenhänge innerhalb der Gestalt eines Dreiecks. Ptolemäus erweiterte diese Kenntnisse. Von ihm stammt auch eine erste Übertragung auf geographische Zwecke: Er bestimmte mehrere tausend Orte auf der Erde mit Winkelkoordinaten.

Im Mittelalter wurden die Erkenntnisse auch in Europa wieder aufgegriffen, vermutlich durch Kontakt mit Arabern. Zuerst wurden die Kenntnisse lediglich für die Astronomie genutzt, doch im späten 16. bzw. frühen 17. Jahrhundert wurde beispielsweise durch B. Pitiscus eine Anwendung im Bereich der Geodäsie und Geographie erdacht.

Zuerst setzte Willebrord van Roijen Snell (Snellius; 1580-1626) dies um, um mit der Methode der Triangulation die Länge eines Meridianbogens und damit auch den Erdumfang zu messen. Wegen einiger Mess- und Rechenfehler war das Ergebnis noch relativ ungenau.

Nach einigen weiteren Landvermessern, die diese Methode anwandten, kam es zum Ende des 17. Jahrhunderts zum Durchbruch der Triangulation in der Landvermessung. Erste europaweite Triangulationsnetze entstanden, wobei als Vorreiter hier sicherlich Jean Picard (1620-1680) und die Familie Cassini zu sehen sind. Detaillierte und besonders genaue Aufnahmen wie die Tranchot – v. Müfflingische Karte oder die Triangulation des Königreichs Hannover entstanden vor allem zu Beginn des 19. Jahrhunderts, gerade im Zuge der Etablierung konventioneller Verwaltungen der europäischen Staaten, z.B. in Preußen. Europaweit institutionalisiert wurde die Landvermessung durch Triangulation als sich 1864 und später verschiedene Staaten mit dem Vertrag zur „Mitteleuropäischen Gradmessung“ zu gegenseitiger Kooperation, Nachmessungen und Neuordnungen verpflichteten.

Noch heute stellt die Triangulation die Basis für die Landvermessung dar. Ortsbestimmungen erfolgen heute allerdings meist über satellitengestützte Systeme (GPS). Entfernungsmessungen werden seit den 1980er Jahren oftmals durch elektronische Distanzmessgeräte durchgeführt. Oftmals werden die Ergebnisse der verschiedenen Messverfahren kombiniert.

Siehe auch

• Vermessungsnetz
• Geodäsie
• Netz (Geodäsie)
• Struve-Bogen
• Großenhainer Grundlinie
• Rauenberg (Trigonometrischer Punkt)
• Königlich-Sächsische Triangulation

Literatur

• G. Grosjean: Geschichte der Kartographie. Bern 1996
• W. Grossmann: Geodätische Rechnungen und Abbildungen in der Landesvermessung. Hannover 1949
• Lexikon zur Geschichte der Kartographie. Von den Anfängen bis zum Ersten Weltkrieg. Wien 1986
• G. Hake, D. Grünreich: Kartographie. Berlin 1994

Weblinks

• AlpenTunnel.de: Praxis im 19. Jhd