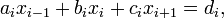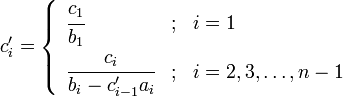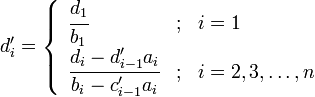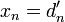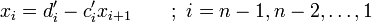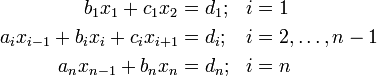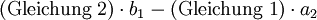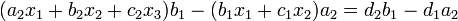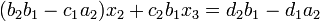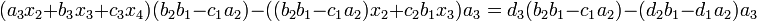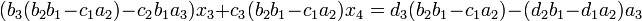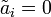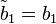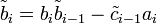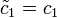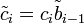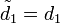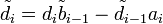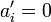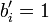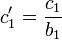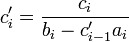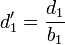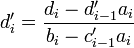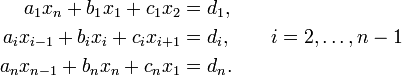Tridiagonalmatrix-Algorithmus

Der Thomas-Algorithmus oder auch Tridiagonalmatrix-Algorithmus (TDMA) ist eine vereinfachte Form des Gaußschen Eliminationsverfahren, der zum schnellen Lösen von linearen Gleichungssystemen mit einer Tridiagonalmatrix benutzt wird.

Ein tridiagonales System mit n Unbekannten kann geschrieben werden als

$a_i x_{i - 1} + b_i x_i + c_i x_{i + 1} = d_i , \,\!$

wobei gelten soll: 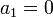$a_1 = 0\,$ und $c_n = 0\,$.

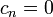In Matrizenform wird das System geschrieben als: $\left[ \begin{matrix} {b_1} & {c_1} & { } & { } & { 0 } \\ {a_2} & {b_2} & {c_2} & { } & { } \\ { } & {a_3} & {b_3} & \cdot & { } \\ { } & { } & \cdot & \cdot & {c_{n-1}}\\ { 0 } & { } & { } & {a_n} & {b_n}\\ \end{matrix} \right] \left[ \begin{matrix} {x_1 } \\ {x_2 } \\ \cdot \\ \cdot \\ {x_n } \\ \end{matrix} \right] = \left[ \begin{matrix} {d_1 } \\ {d_2 } \\ \cdot \\ \cdot \\ {d_n } \\ \end{matrix} \right].$

Für solche Systeme kann die Lösung nach O(n) Operationen gefunden wird, statt nach O(n³) mit dem Gaußschen Eliminationsverfahren. Ein erster Durchlauf eliminiert die a_i's, anschließend erhält man die Lösung mit Hilfe eines Rückwärts-Einsetzverfahrens. Beispiele für diese Matrizen entstehen üblicherweise aus der Diskretisierung der eindimensionalen Poisson-Gleichung (z.B. eindimensionale Diffusionsprobleme) und aus der natürlichen kubischen Spline-Interpolation.

Das Verfahren

Der erste Schritt ist es, die Koeffizienten folgendermaßen zu modifizieren. Die "neuen" modifizierten Koeffizienten sind mit einem Strich gekennzeichnet.

$c'_i = \begin{cases} \begin{array}{lcl} \cfrac{c_1}{b_1} & ; & i = 1 \\ \cfrac{c_i}{b_i - c'_{i - 1} a_i} & ; & i = 2, 3, \dots, n - 1 \\ \end{array} \end{cases} \,$

$d'_i = \begin{cases} \begin{array}{lcl} \cfrac{d_1}{b_1} & ; & i = 1 \\ \cfrac{d_i - d'_{i - 1} a_i}{b_i - c'_{i - 1} a_i} & ; & i = 2, 3, \dots, n \\ \end{array} \end{cases} \,$

Dies ist der vorwärts gerichtete Durchlauf. Die Lösung ergibt sich dann durch ein Rückwärts-Einsetzverfahren:

$x_n = d'_n\,$

$x_i = d'_i - c'_i x_{i + 1} \qquad ; \ i = n - 1, n - 2, \ldots, 1$

Herleitung

Die Unbekannten seien 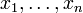$x_1,\ldots, x_n$. Die zu lösenden Gleichungen seien:

$\begin{align} b_1 x_1 + c_1 x_2 & = d_1;& i & = 1 \\ a_i x_{i - 1} + b_i x_i + c_i x_{i + 1} & = d_i;& i & = 2, \ldots, n - 1 \\ a_n x_{n - 1} + b_n x_n & = d_n;& i & = n \end{align}$

Die zweite Gleichung (i = 2) wird nun wie folgt mit der ersten Gleichung modifiziert:

$(\mbox{Gleichung 2}) \cdot b_1 - (\mbox{Gleichung 1}) \cdot a_2$

Dies ergibt:

$(a_2 x_1 + b_2 x_2 + c_2 x_3) b_1 - (b_1 x_1 + c_1 x_2) a_2 = d_2 b_1 - d_1 a_2 \,$

$(b_2 b_1 - c_1 a_2) x_2 + c_2 b_1 x_3 = d_2 b_1 - d_1 a_2 \,$

Dadurch wurde x₁ aus der zweiten Gleichung eliminiert. Mit einer analogen Vorgehensweise ergibt sich aus der modifizierten zweiten und der dritten Gleichung:

$(a_3 x_2 + b_3 x_3 + c_3 x_4) (b_2 b_1 - c_1 a_2) - ((b_2 b_1 - c_1 a_2) x_2 + c_2 b_1 x_3) a_3 = d_3 (b_2 b_1 - c_1 a_2) - (d_2 b_1 - d_1 a_2) a_3 \,$

$(b_3 (b_2 b_1 - c_1 a_2) - c_2 b_1 a_3 )x_3 + c_3 (b_2 b_1 - c_1 a_2) x_4 = d_3 (b_2 b_1 - c_1 a_2) - (d_2 b_1 - d_1 a_2) a_3 \,$

Jetzt wurde x₂ eliminiert. Wird diese Vorgehensweise bis zur n-ten Zeile wiederholt, enthält die modifizierte n-te Gleichung nur eine Unbekannte enthalten. Diese Gleichung wird nun gelöst und das Ergebnis genutzt, um die (n − 1)-te Gleichung zu lösen. Dies wird so lange fortgeführt bis alle Unbekannten bekannt sind.

Verständlicherweise werden die Koeffizienten mit jedem Schritt komplizierter, wenn sie explizit dargestellt werden. Die Koeffizienten können jedoch auch rekursiv dargestellt werden:

$\tilde a_i = 0\,$

$\tilde b_1 = b_1\,$

$\tilde b_i = b_i \tilde b_{i - 1} - \tilde c_{i - 1} a_i\,$

$\tilde c_1 = c_1\,$

$\tilde c_i = c_i \tilde b_{i - 1}\,$

$\tilde d_1 = d_1\,$

$\tilde d_i = d_i \tilde b_{i - 1} - \tilde d_{i - 1} a_i\,$

Um den Lösungsprozess weiter zu beschleunigen, wird 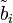$\tilde b_i$ heraus dividiert (wenn 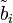$\tilde b_i$) ≠ 0). Die neuen Koeffizienten lauten:

$a'_i = 0\,$

$b'_i = 1\,$

$c'_1 = \frac{c_1}{b_1}\,$

$c'_i = \frac{c_i}{b_i - c'_{i - 1} a_i}\,$

$d'_1 = \frac{d_1}{b_1}\,$

$d'_i = \frac{d_i - d'_{i - 1} a_i}{b_i - c'_{i - 1} a_i}\,$

Dies ergibt:

$\begin{array}{lcl} x_i + c'_i x_{i + 1} = d'_i \qquad &;& \ i = 1, \ldots, n - 1 \\ x_n = d'_n \qquad &;& \ i = n \\ \end{array} \,$

Die letzte Gleichung enthält nur eine Unbekannte. Bestimmt man sie, reduziert man die Anzahl der Unbekannten in der vorletzten Gleichung auf eins, so dass dieses Rückwärts-Einsetzverfahren genutzt werden kann, um alle Unbekannten zu bestimmen.

$x_n = d'_n\,$

$x_i = d'_i - c'_i x_{i + 1} \qquad ; \ i = n - 1, n - 2, \ldots, 1$

Varianten

In manchen Situationen, insbesondere in solchen mit periodischen Grenzbedingungen, kann es sein, dass eine leicht veränderte Form des tridiagonalen Systems zu lösen ist:

$\begin{align} a_1 x_{n} + b_1 x_1 + c_1 x_2 & = d_1, \\ a_i x_{i - 1} + b_i x_i + c_i x_{i + 1} & = d_i,\quad\quad i = 2,\ldots,n-1 \\ a_n x_{n-1} + b_n x_n + c_n x_1 & = d_n. \end{align}$

In diesem Fall kann die Sherman-Morrison-Formel benutzt werden, um die zusätzlichen Operationen des Gaußschen Eliminationsverfahren zu vermeiden und dennoch den Thomas-Algorithmus nutzen zu können.

In anderen Fällen kann das Gleichungssystem block-tridiagonal sein, d.h. dass die Elemente des obigen Gleichungssystems kleinere Untermatrizen sind (z.B. bei der zweidimensionalen Poisson-Gleichung). Für diese Fälle wurden ebenfalls vereinfachte Varianten der Gauß-Elimination entwickelt.

Eine Variante des Thomas-Algorithmus ist der Hu-Gallash-Algorithmus, der, statt des Rückwärts-Einsetzverfahren, ein Vorwärts-Einsetzverfahren nutzt.

Einzelnachweise

• Conte, S.D., and deBoor, C.: Elementary Numerical Analysis. McGraw-Hill, New York. 1972

Weblinks

• Thomas-Algorithmus für — SCILAB (franz.)
• Implementierung in C und C# (engl.)