- Trippelsort
-
Stooge sort (auch Trippelsort) ist ein rekursiver Sortieralgorithmus nach dem Prinzip Teile und herrsche (divide and conquer).
Inhaltsverzeichnis
Prinzip
- Sind das erste und das letzte Element nicht in der richtigen Reihenfolge, so werden sie vertauscht.
- Sind mehr als zwei Elemente in der Liste, fortsetzen, ansonsten abbrechen.
- Sortiere die ersten zwei Drittel der Liste
- Sortiere die letzten zwei Drittel der Liste
Komplexität
Der Algorithmus besitzt eine im Vergleich zu anderen Sortieralgorithmen sehr schlechte Worst-Case-Laufzeit, in der Informatik wird dies mittels Landau-Symbol durch
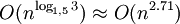 ausgedrückt. Da selbst Bubblesort ein besseres Laufzeitverhalten besitzt, ist Stoogesort nur zur Anschauung von Interesse.
ausgedrückt. Da selbst Bubblesort ein besseres Laufzeitverhalten besitzt, ist Stoogesort nur zur Anschauung von Interesse.Pseudocode
Der folgende Pseudocode sortiert die Eingabemenge aufsteigend.
A: Liste (Array) mit der unsortierten Eingabemenge i: Linke Grenze des zu sortierenden Ausschnitts des Arrays j: Rechte Grenze des zu sortierenden Ausschnitts des Arrays stoogesort(A,i,j) 1 if A[i] > A[j] 2 then A[i]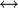 A[j]
3 if i+1
A[j]
3 if i+1 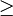 j
4 then return
5 k
j
4 then return
5 k 
 (j-i+1)/3
(j-i+1)/3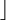 6 stoogesort(A,i,j-k)
6 stoogesort(A,i,j-k)  Sortieren der ersten zwei Drittel
7 stoogesort(A,i+k,j)
Sortieren der ersten zwei Drittel
7 stoogesort(A,i+k,j)  Sortieren der letzten zwei Drittel
8 stoogesort(A,i,j-k)
Sortieren der letzten zwei Drittel
8 stoogesort(A,i,j-k)  Sortieren der ersten zwei Drittel
Sortieren der ersten zwei Drittel
Implementierung
Java
// Interface-Methode (um den Aufruf mit den richtigen Startwerten zu erzwingen) public void stoogeSort(int[] a) { stoogeSort(a,0,a.length); } // Interne Methode private void stoogeSort(int[] a,int s,int e) { if(a[e-1]<a[s]) { int temp=a[s]; a[s]=a[e-1]; a[e-1]=temp; } int len=e-s; if(len>2) { int third=len/3; // Zur Erinnerung: Dies ist die (abgerundete) Integer-Division stoogeSort(a,s,e-third); stoogeSort(a,s+third,e); stoogeSort(a,s,e-third); } }Visual Basic
Sub StoogeSort(ByVal Left As Integer, ByVal Right As Integer) If Feld(Left) > Feld(Right) Then Temp = Feld(Left) Feld(Left) = Feld(Right) Feld(Right) = Temp End If If Right - Left >= 2 Then Call StoogeSort(Left, Left + (Right - Left) * 2 / 3) Call StoogeSort(Left + (Right - Left) * 1 / 3, Right) Call StoogeSort(Left, Left + (Right - Left) * 2 / 3) End If End SubKorrektheitsbeweis
Beweis durch Vollständige Induktion (Zeilennummer beziehen sich auf den oben angegebenen Pseudocode): Induktionsanfang
Für Länge des Arrays n=1 und n=2 sortiert Stoogesort korrekt, da in Zeile 1-4 des Algorithmus die Elemente der Liste in die richtige Reihenfolge gebracht werden und der Algorithmus an der Stelle abbricht.
Induktionsschluss
Aus der Induktionsvoraussetzung folgt, dass die Aufrufe in Zeilen 6-8 korrekt sortierte Teilarrays liefern. Elemente im i-ten Drittel einer korrekten Sortierung des Arrays heißen Typi-Elemente, i=1,2,3.
Nach der Sortierung der ersten zwei Drittel in Zeile 6 befindet sich kein Typ3-Element mehr im ersten Drittel der Liste.
Nach der Sortierung der letzten zwei Drittel in Zeile 7 stehen im letzten Drittel der Liste alle Typ3-Elemente in sortierter Reihenfolge.
Nach der erneuten Sortierung der ersten zwei Drittel in Zeile 8 stehen jetzt außerdem alle Typ1- und Typ2-Elemente in sortierter Reihenfolge.
Weblinks
Siehe auch: Liste von Algorithmen
Wikimedia Foundation.
