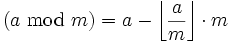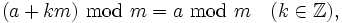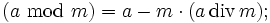- Uhrenarithmetik
-
Modulo [ˈmoːduloː] (lat. Modulus, Kasus Ablativ: "durch Maß" oder auch "mit Maß", somit Mehrzahl Moduli), mathematisches Formelzeichen mod, in vielen Programmiersprachen durch % wiedergegeben, ist eine mathematische Funktion, die den Rest aus der Division zweier ganzer Zahlen angibt. Eine weiterführende Modulorechnung existiert auch für Polynome, die auf den Mengen sog. Galoiskörper definiert sind. Der Rest ist in dem Fall ein Polynom.
- Beispiel: 7 mod 2 = 1, Sprechweise: „Sieben modulo zwei gleich eins.“ Denn 7 : 2 = 3, Rest 1 (2 · 3 + 1 = 7). Ebenso ist beispielsweise 7 mod 3 = 1.
Inhaltsverzeichnis
Varianten der Modulo-Funktion
Es gibt zwei Varianten der Modulo-Funktion, die für negative Argumente unterschiedliche Ergebnisse liefern:
- „Mathematische Variante“:
-
- Die Gaußklammer
 bezeichnet die größte ganze Zahl, die kleiner oder gleich der Zahl in der Gaußklammer ist, also ohne den Rest der Division
bezeichnet die größte ganze Zahl, die kleiner oder gleich der Zahl in der Gaußklammer ist, also ohne den Rest der Division 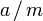 . Für diese Variante gilt stets
. Für diese Variante gilt stets
- aber im Allgemeinen ist
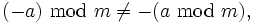 z. B.
z. B. 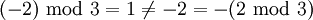 .
.
- Ist m positiv, so ist
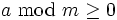 für alle a.
für alle a.
- „Symmetrische Variante“:
-
- dabei bezeichnet
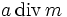 den zur Null hin gerundeten Quotienten
den zur Null hin gerundeten Quotienten 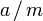 . Für diese Variante gilt
. Für diese Variante gilt
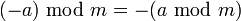 ,
,
- aber im Allgemeinen
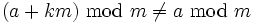 , z. B.
, z. B. 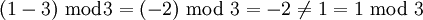 .
.
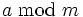 hat stets dasselbe Vorzeichen wie a, oder es gilt
hat stets dasselbe Vorzeichen wie a, oder es gilt 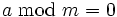 .
.
In Programmiersprachen ist üblicherweise die zweite Variante implementiert. Gilt
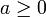 und m > 0, so ergeben beide Varianten dasselbe Ergebnis.
und m > 0, so ergeben beide Varianten dasselbe Ergebnis.Beispiele:
- 17 mod 3 = 2, da 17 = 5×3 + 2 („drei passt fünf mal in 17 und es bleiben zwei übrig“ – der Rest ist also zwei)
- 2 mod 3 = 2, da 2 = 0×3 + 2
- 3 mod 3 = 0, da 3 = 1×3 + 0
Wenn
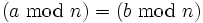 , dann folgt nicht daraus, dass a = b ist, sondern nur, dass sich a und b um ein ganzzahliges Vielfaches von n unterscheiden, also:
, dann folgt nicht daraus, dass a = b ist, sondern nur, dass sich a und b um ein ganzzahliges Vielfaches von n unterscheiden, also: 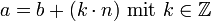 Eine derartige Gleichung kann auch einfacher mit Hilfe der in der Zahlentheorie verbreiteten Kongruenzrelation geschrieben werden.
Eine derartige Gleichung kann auch einfacher mit Hilfe der in der Zahlentheorie verbreiteten Kongruenzrelation geschrieben werden.Anwendung
Programmierung:
Modulo wird in der Programmierung relativ häufig verwendet. Mit mod kann geprüft werden, ob eine Zahl gerade ist: if ( (x mod 2) == 0), dann ist x gerade. Modulo kann man immer benutzen, wenn man alle X Schleifendurchläufe einen speziellen Programmcode ausführen will. Auch bei vielen Berechnungen und Algorithmen ist er sinnvoll einsetzbar. Allgemein kann man mit mod prüfen, ob eine Zahl durch eine andere genau teilbar ist, dann ist der Modulo nämlich Null. Andersrum muss man in der Programmierung oft auf ganze Vielfache von einer Zahl ergänzen (z. B. 4 Bytes) und bekommt durch den Modulo heraus, wie viele „Pad-Bytes“ noch fehlen.
- Beispiel: Man programmiert eine Uhr und hat die Zeit als Sekundenwert seit 0 Uhr gegeben. Dann kann man den Sekundenwert Mod 3600 berechnen. Ist dieser gleich 0, so weiß man, dass eine volle Stunde angefangen hat. Diese Information kann man nutzen, um z. B. ein akustisches Signal (Gong zur vollen Stunde) auszulösen. Mit der Berechnung Sekundenwert Mod 60 erhält man die Sekunde in der aktuellen Minute, die oftmals von Digitaluhren als letzte zwei Stellen anzeigt werden.
Weitere Anwendungen:
- Zur Berechnung der Prüfziffer der ISBN, siehe als Beispiel ISBN → Formeln zur Berechnung der Prüfziffer
- Modulo 10
- In der Kalenderberechnung (z. B. die relativ komplizierte Berechnung des Osterdatums)
- Bei der International Bank Account Number (IBAN)
- In der Kryptografie, z. B. beim Diffie-Hellman-Schlüsselaustausch
Literatur
- K. Reiss, G. Schmieder: Basiswissen Zahlentheorie – Eine Einführung in Zahlen und Zahlenbereiche. Springer-Verlag, Berlin, Heidelberg, New York, ISBN 3-540-21248-5.
Siehe auch
- Kongruenz (Zahlentheorie)
- Hash-Funktion und die dort genannten Verfahren
- Kleiner fermatscher Satz
- Satz von Euler
- Dualsystem
- Galoiskörper
Weblinks
Wikimedia Foundation.