Umgebungsdiagramme

Umgebungsdiagramme dienen der grafischen Veranschaulichung der Umgebungsmodelle von funktionalen Programmiersprachen wie LISP oder Scheme. Sie finden insbesondere didaktische Verwendung, um die Unterschiede zwischen statischem und dynamischem Binden zu verdeutlichen. Umgebungsdiagramme basieren auf dem Buchkapitel The Environment Model of Evaluation (Structure and Interpretation of Computer Programs, Abelson and Sussman).

Umgebungsmodell

Die Struktur eines Programms lässt sich in einzelne Umgebungen (env₀...env_k) zerlegen.

• env₀ stellt dabei die initiale Umgebung dar. Sie stellt die Grundfunktionalität (arithmetische Funktionen und andere Operatoren, z.B. +, -, =) einer Sprache dar. env₀ ist immer vorhanden und wird implizit vorausgesetzt („User Global Environment“). Alle anderen Umgebungen stützen sich direkt oder indirekt auf env₀ ab.
• env₁ ist das Haupt- oder Rahmenprogramm („User Initial Environment“). env₁ enthält Funktions- und Variablendeklarationen. Erst durch den Aufruf einer Funktion oder durch let bzw. let*, wird eine „höhere“ Umgebung env₂ erstellt.
• env₂... env_k sind gleichwertig zu env1. Eine Umgebung env₂ kann selbst wiederum eigene Funktionen (Methoden) oder Variablen (Attribute) deklarieren. Auch hier führt ein Funktionsaufruf zu einer Inkrementierung der Umgebungsstufe.
• Umgebungen lassen sich verschachteln (bei Scheme durch lambda, let und define).

Beispiel (Scheme)

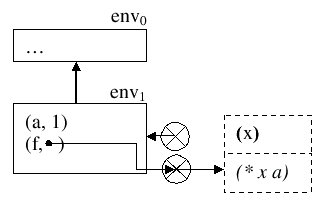
(define a 1) ;env₁: a->1

(define (f x) (* x a)) ;env₁: f->(* x a), a->1, x->5

(f 5) ;Funktionsaufruf: neue Umgebung env₂ wird erstellt

Elemente von Umgebungsdiagrammen

Folgende Elemente tauchen im Umgebungsdiagramm auf:

Rechtecke

Rechtecke stellen eine Umgebung dar, welche Bindungspaare enthält.

Gestrichelte Rechtecke

Gestrichelte Rechtecke stellen einen Funktionsrumpf dar. Im oberen Teil eines solchen Rechtecks werden die Parameter einer Funktion in Klammern geschrieben. Im unteren Teil folgt dann der eigentliche Funktionsterm. Funktionsterme können selbst wiederum andere Funktionen aufrufen oder let- und let*-Ausdrücke enthalten, wodurch eine neue Umgebung erstellt wird.

Kreispaare

Kreispaare stehen für Funktionsobjekte. Einer der Kreise der Kreispaare verweist auf den Funktionsrumpf des Funktionsobjekts. Der zweite Kreis zeigt auf die Definitionsumgebung, also auf die Umgebung, in der die Funktion definiert wurde (in aller Regel also eine Umgebungsebene niedriger).

Pfeile oder Kanten

Gerichtete Kanten referenzieren vom Funktionsobjekt auf die Definitionsumgebung und auf den Funktionsrumpf.

Beispiel für ein Umgebungsdiagramm

Das obige Code-Beispiel sähe in einem Umgebungsdiagramm folgendermaßen aus:

Beispiel eines einfachen Umgebungsdiagramms von

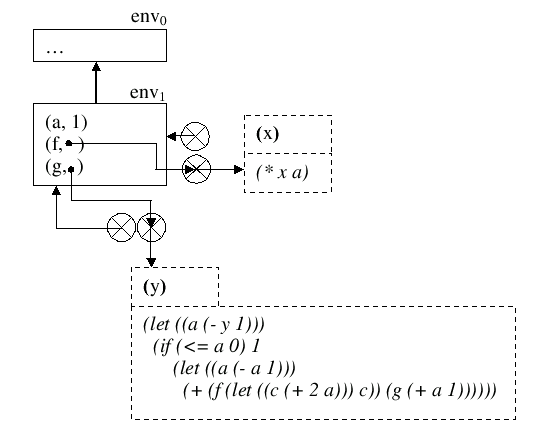
Weiterführung des Beispiels

Aufbauend auf dem letzten Beispiel folgt hier eine Erweiterung und Vervollständigung:

Scheme-Code:

(define a 1) ;env1: a->1

(define (f x) (* x a)) ;env1: f->(* x a), a->1, x->5

((lambda (a) (if (<= a 0) 1

         ((lambda (a) (+ (f ((lambda (c) c) (+ 2 a))) (g (+ a 1))))

     (- a 1))))

   (- y 1)))

Umgebungsdiagramm:

Umgebungsdiagramm des weiterführenden Beispiels

Rezept zum Erstellen eines Umgebungsdiagramms

(Umgebungsdiagramme für Dummies)

1. Man braucht für die Umgebung env₀ kein Rechteck anzufertigen, man notiert also als erstes "env0".

2. Man notiere die äußersten Funktionen und Bindungen in die erste Umgebung env_0.

Neue Umgebungen werden durch folgende Konstrukte erzeugt:
- let und let*
- define
- ...
Dabei ist zu beachten, daß bei jeder Prozedurauswertung eine neue Umgebung erstellt wird.

3. Funktionen werden durch 2 Kreise als Funktionsobjekt, mit Hilfe von 3 Pfeilen, an die alte Umgebung angebunden. Der erste Pfeil zeigt von dem Parameter der Funktion (welcher durch eine Lücke repräsentiert wird) auf den Rand des linken Kreises. Der zweite Pfeil zeigt von der Mitte des linken Kreises auf den Rand der Funktionsumgebung (welche nicht mit env_N durchnummeriert wird). Der dritte Pfeil führt aus der Mitte des rechten Kreises zum Rand der Umgebung, in der die Funktion definiert wurde.

Einzeichnen des konkreten Ablaufs des repräsentierten Programms

Quellen

• Prof. Klaus Hinrichs: Informatik-1-Vorlesungsskript an der Universität Münster zur Scheme-Programmierung