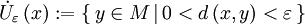- Umgebungsfilter
-
Umgebung ist ein Begriff der Mathematik, der in der Topologie allgemein definiert wird und auch in weiteren Teilgebieten wie der Analysis verwendet wird. Er ist eine Verallgemeinerung des Begriffs der ε-Umgebung aus der reellen Analysis.
Mathematische Eigenschaften, die auf eine gewisse Umgebung bezogen sind, heißen lokal, im Unterschied zu global.
Inhaltsverzeichnis
Umgebungen in topologischen Räumen
Eine Teilmenge U eines topologischen Raumes
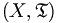 heißt Umgebung des Punktes
heißt Umgebung des Punktes  , falls eine offene Menge O mit
, falls eine offene Menge O mit 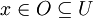 existiert.
existiert.Die Menge aller Umgebungen eines Punktes x bildet einen Filter
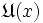 , der Umgebungsfilter von x heißt. Der Umgebungsfilter ist eine Teilmenge der Potenzmenge von X.
, der Umgebungsfilter von x heißt. Der Umgebungsfilter ist eine Teilmenge der Potenzmenge von X.Eine Teilmenge
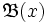 von
von 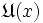 heißt eine Umgebungsbasis von x, wenn jede Umgebung von x ein Element von
heißt eine Umgebungsbasis von x, wenn jede Umgebung von x ein Element von 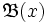 als Teilmenge hat.
als Teilmenge hat.Eine Teilmenge U eines topologischen Raumes X heißt Umgebung der Menge
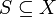 , falls eine offene Menge O mit
, falls eine offene Menge O mit 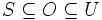 existiert.
existiert.Manchmal wird stattdessen gefordert, dass eine Umgebung (eines Punktes oder einer Teilmenge) selbst schon offen ist.
Eigenschaften
Für die Umgebungen gelten folgende Eigenschaften (Querenburg, 1979, S. 20):
- Ist
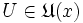 , so gilt
, so gilt 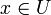 . (Jede Umgebung eines Punktes enthält den Punkt.)
. (Jede Umgebung eines Punktes enthält den Punkt.) - Ist
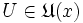 und
und 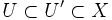 , so ist auch
, so ist auch 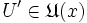 . (Jede Obermenge einer Umgebung eines Punktes ist wieder Umgebung des Punktes.)
. (Jede Obermenge einer Umgebung eines Punktes ist wieder Umgebung des Punktes.) - Ist
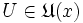 und
und 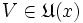 , so gilt auch
, so gilt auch 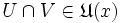 . (Die Schnittmenge zweier Umgebungen eines Punktes ist wieder Umgebung des Punktes. Damit ist auch die Schnittmenge einer endlichen Menge von Umgebungen eines Punktes wieder Umgebung des Punktes.)
. (Die Schnittmenge zweier Umgebungen eines Punktes ist wieder Umgebung des Punktes. Damit ist auch die Schnittmenge einer endlichen Menge von Umgebungen eines Punktes wieder Umgebung des Punktes.) - Zu jedem
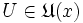 existiert ein
existiert ein 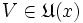 , so dass
, so dass 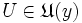 für jedes
für jedes 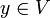 gilt. (Die Umgebung eines Punktes kann gleichzeitig Umgebung anderer in ihr enthaltener Punkte sein. Im allgemeinen ist eine Umgebung U eines Punktes x nicht Umgebung aller in ihr enthaltenen Punkte, sie enthält aber eine weitere Umgebung V von x, so dass U Umgebung aller Punkte in V ist.)
gilt. (Die Umgebung eines Punktes kann gleichzeitig Umgebung anderer in ihr enthaltener Punkte sein. Im allgemeinen ist eine Umgebung U eines Punktes x nicht Umgebung aller in ihr enthaltenen Punkte, sie enthält aber eine weitere Umgebung V von x, so dass U Umgebung aller Punkte in V ist.)
Ordnet man dagegen jedem Punkt x einer Menge X ein die obigen Bedingungen erfüllendes Mengensystem
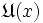 zu, so gibt es eine eindeutig bestimmte Topologie auf X, so dass für jedes x das System
zu, so gibt es eine eindeutig bestimmte Topologie auf X, so dass für jedes x das System 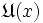 das Umgebungssystem von x ist. Eine Menge ist in diesem Fall genau dann offen, wenn sie mit jedem ihrer Punkte auch eine Umgebung dieses Punktes enthält. (Dieser Satz motiviert die Verwendung des Wortes „offen“ für den oben definierten mathematischen Begriff: Jeder Punkt nimmt seine nächsten Nachbarn in die offene Menge mit, keiner steht anschaulich gesprochen „am Rand“ der Menge.)
das Umgebungssystem von x ist. Eine Menge ist in diesem Fall genau dann offen, wenn sie mit jedem ihrer Punkte auch eine Umgebung dieses Punktes enthält. (Dieser Satz motiviert die Verwendung des Wortes „offen“ für den oben definierten mathematischen Begriff: Jeder Punkt nimmt seine nächsten Nachbarn in die offene Menge mit, keiner steht anschaulich gesprochen „am Rand“ der Menge.)ε-Umgebungen in metrischen Räumen
In einem Metrischen Raum (M, d) ergibt sich der Umgebungsbegriff aus der Metrik d: Man definiert die sogenannten ε-Umgebungen. Für jeden Punkt x des Raums M und jede positive reelle Zahl ε wird definiert:
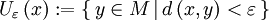
Die so definierte ε-Umgebung von x wird auch offene ε-Kugel um x oder offener Ball genannt.
Eine Teilmenge von M ist nun genau dann eine Umgebung des Punktes x, wenn sie eine ε-Umgebung von x umfasst. Die so definierten Umgebungen erfüllen die oben aufgeführten Axiome 1 bis 4 und bestimmen damit auf der Menge M eindeutig eine Topologie: die durch die Metrik induzierte Topologie. Verschiedene Metriken können denselben Umgebungsbegriff und damit dieselbe Topologie induzieren.
Beispiele
- Die Menge der reellen Zahlen wird durch den Betrag als Norm zu einem metrischen Raum. Die ε-Umgebung einer Zahl x ist das offene Intervall ]x-ε,x+ε[.
- Die Menge der komplexen Zahlen wird ebenso zum metrischen Raum. Die ε-Umgebung einer Zahl z ist die offene Kreisscheibe um z vom Radius ε.
- Etwas allgemeiner tragen alle n-dimensionalen reellen Vektorräume durch den üblichen (von der Quadratnorm induzierten) Abstandsbegriff eine Metrik und damit eine natürliche Topologie. Die ε-Umgebungen sind hier n-dimensionale Kugeln (im geometrischen Sinn) vom Radius ε. Dies motiviert die allgemeinere Sprechweise von ε-Kugeln auch in anderen metrischen Räumen.
- Ein wichtiges Beispiel aus der reellen Analysis: Der Raum der beschränkten Funktionen auf einem reellen Intervall I wird durch die Supremumsnorm zu einem metrischen Raum. Die ε-Umgebung einer beschränkten Funktion f auf I besteht hier aus allen Funktionen, die f punktweise mit einer kleineren Abweichung als ε approximieren. Anschaulich: Die Schaubilder aller dieser Funktionen liegen innerhalb eines „ε-Schlauches“ um das Schaubild von f herum.
Punktierte Umgebung
Eine punktierte Umgebung
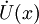 eines Punktes x entsteht aus einer Umgebung
eines Punktes x entsteht aus einer Umgebung 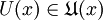 , indem man den Punkt x entfernt, also
, indem man den Punkt x entfernt, also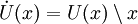 .[1]
.[1]
Punktierte Umgebungen spielen insbesondere bei der Definition des Grenzwerts einer Funktion eine Rolle, ebenso in der Funktionentheorie bei der Betrachtung von Wegintegralen holomorpher Funktionen.
Beispiel
In einem metrischen Raum (M, d) sieht eine punktierte ε-Umgebung folgendermaßen aus:
Einzelnachweise
- ↑ H. Heuser, Lehrbuch der Analysis, Teil 1, 8. Auflage 1990. ISBN 3-519-12231-6. S. 236
Literatur
- Boto von Querenburg: Mengentheoretische Topologie. 3. Auflage. Springer-Verlag, 2001, ISBN 3-540-09799-6
- James Munkres: Topology. 2. Auflage. Prentice Hall, 1999, ISBN 0-13-181629-2
- Ist
Wikimedia Foundation.