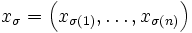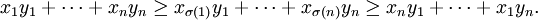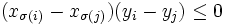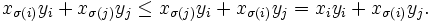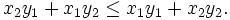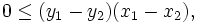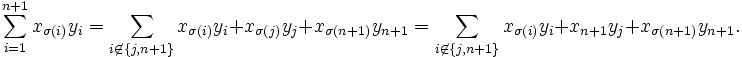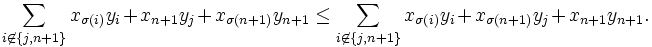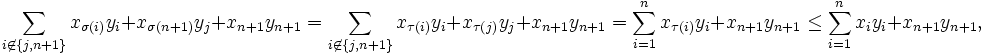- Umordnungsungleichung
-
In der Mathematik ist die Umordnungs-Ungleichung eine Aussage über die Veränderung des Wertes von formalen Skalarprodukten durch Umordnung.
Gegeben seien zwei n-Tupel reeller Zahlen
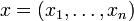 und
und 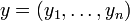 mit
mit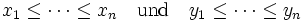 .
.
Das Tupel
sei eine Permutation des Tupels x. Fasst man nun die n-Tupel als Vektoren auf und betrachtet deren Skalarprodukt, so besagt die Umordnungs-Ungleichung, dass
Das Skalarprodukt ist also maximal, wenn die Elemente der n-Tupel gleich geordnet sind, und minimal, wenn sie entgegengesetzt geordnet sind.
Man beachte, dass im Gegensatz zu vielen anderen Ungleichungen keine Voraussetzungen für die Vorzeichen von xi und yi notwendig sind.
Inhaltsverzeichnis
Beweise
Beweis mittels Vertauschungen
Die Beweisidee besteht darin, das kleinste i, das
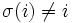 erfüllt und jenes j mit i = σ(j) zu betrachten. Dann sind also σ(i) > i und j > i, daher gilt
erfüllt und jenes j mit i = σ(j) zu betrachten. Dann sind also σ(i) > i und j > i, daher gilt 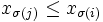 und
und 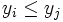 , also
, alsound daher
Solange also ein i mit
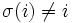 existiert, lässt sich die Summe für gleich geordnete Tupel vergrößern.
existiert, lässt sich die Summe für gleich geordnete Tupel vergrößern.Analog zeigt man, dass sich die Summe für entgegengesetzt geordnete Tupel verkleinern lässt, solange ein i mit
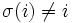 existiert.
existiert.Beweis mit Induktion
Dieser Beweis lässt sich ausführlicher auch mit vollständiger Induktion führen. Für den Induktionsanfang n = 2 gibt es nur zwei Permutationen, es ist also zu zeigen, dass
Das ist aber äquivalent zu
also zur Voraussetzung, dass beide Tupel gleich geordnet sind.
Im Induktionsschritt sei nun j der Index mit σ(j) = n + 1. Der Fall j = n + 1 ist einfach zu behandeln, sei also
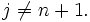 Dann gilt
Dann giltNun wendet man den im Induktionsanfang bewiesenen Fall n = 2 an und erhält
Definiert man nun für
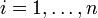 die Permutation
die Permutationso ergibt sich aus der Induktionsvoraussetzung
also genau die Behauptung für das Maximum des Skalarprodukts.
Der Beweis für das Minimum des Skalarprodukts ist analog.
Anwendungen
Viele bekannte Ungleichungen lassen sich aus der Umordnungs-Ungleichung beweisen, beispielsweise die Ungleichung vom arithmetischen und geometrischen Mittel, Cauchy-Schwarzsche Ungleichung und die Tschebyschow-Summenungleichung.
Literatur
- G. H. Hardy, J. E. Littlewood, G. Polya: Inequalities, Cambridge University Press (1952), Kapitel 10.2.
Wikimedia Foundation.