Uneigentliche Gerade

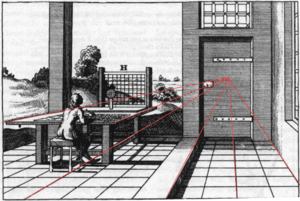Veranschaulichung des Fernpunkts
Vergleichbar dem Fernpunkt treffen sich in der perspektivischen Darstellung Geraden, die in der Wirklichkeit parallel sind, in einem Punkt, dem Fluchtpunkt. Im Gegensatz zum Fluchtpunkt ist der Fernpunkt allerdings kein Punkt der Zeichenebene (also nicht etwa – wie hier der Fluchtpunkt – identisch mit einem Punkt der gezeichneten Tür), sondern befindet sich außerhalb der Menge "realer" Punkte.

Als Fernelemente bezeichnet man die Elemente (Punkte, Geraden und so weiter), die zu einem affinen Raum hinzugefügt werden, um diesen zu einem projektiven Raum zu erweitern:

Ein Fernpunkt (auch: unendlich ferner Punkt oder uneigentlicher Punkt) wird eingeführt als der „Schnittpunkt“ einer Schar paralleler Geraden. Ein Fernpunkt ist also die mathematische Präzisierung der Beobachtung, dass „Parallelen sich im Unendlichen schneiden“. Das Bild eines Fernpunkts in einer perspektivischen Darstellung heißt Fluchtpunkt.

Alle Fernpunkte einer Ebene bilden deren Ferngerade (unendlich ferne Gerade, uneigentliche Gerade).

In der räumlichen Geometrie gibt es je eine Ferngerade zu jeder Schar paralleler Ebenen. Die Ferngeraden zusammen bilden die Fernebene (unendlich ferne Ebene, uneigentliche Ebene).

Weitere Fernebenen und entsprechend höherdimensionale Fernelemente gibt es in Räumen höherer Dimension.