Unerreichbare Kardinalzahl

Dieser Artikel oder Abschnitt bedarf einer Überarbeitung. Näheres ist auf der Diskussionsseite angegeben. Hilf mit, ihn zu verbessern, und entferne anschließend diese Markierung.

In der Mengenlehre wird eine Kardinalzahl als groß bezeichnet, wenn ihre Existenz erwiesenermaßen nicht mit den üblichen Axiomen der Mengenlehre ZFC bewiesen werden kann. Nimmt man die Aussage, dass eine große Kardinalzahl mit einer bestimmten Eigenschaft existiert, als neues Axiom zu ZFC hinzu, erhält man eine stärkere Theorie, in der einige der in ZFC unentscheidbaren Sätze entschieden werden können. Diese Große-Kardinalzahl-Axiome spielen deshalb in der modernen Mengenlehre eine wichtige Rolle.

Die folgende Liste großer Kardinalzahlen ist nach Konsistenzstärke geordnet: Die Existenz einer Kardinalzahl impliziert die Existenz der vor ihr aufgelisteten:

• κ heißt schwach unerreichbare Kardinalzahl, wenn sie überabzählbarer, regulärer Limes ist, wenn also cf(κ) = κ > ω gilt und für jedes μ < κ auch μ ⁺ < κ. Schwach unerreichbare Kardinalzahlen sind genau die regulären Fixpunkte der Aleph-Reihe: $\aleph_\kappa = \kappa = \mathrm{cf} (\kappa)$.
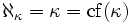• κ heißt stark unerreichbare Kardinalzahl, wenn κ überabzählbarer, regulärer starker Limes ist, wenn also cf(κ) = κ > ω gilt und für jedes μ < κ auch 2^μ < κ. Stark unerreichbare Kardinalzahlen sind genau die regulären Fixpunkte der Beth-Reihe: $\beth_\kappa = \kappa = \mathrm{cf} (\kappa)$.

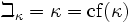Da 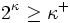$2^\kappa \geq \kappa^+$ ist jede stark unerreichbare Kardinalzahl auch schwach unerreichbar. Ist κ schwach unerreichbar, so ist L_κ ein Modell des Zermelo-Fraenkelschen Axiomensystems der Mengenlehre ZFC, ist κ stark unerreichbar, so ist auch V_κ ein Modell von ZFC. Die Existenz unerreichbarer Kardinalzahlen impliziert also die Widerspruchsfreiheit von ZFC. Nimmt man an, dass ZFC widerspruchsfrei ist, so kann nach dem zweiten Gödelschen Unvollständigkeitssatz nicht in ZFC bewiesen werden, dass es eine unerreichbare Kardinalzahl gibt.

• Eine Mahlo-Kardinalzahl ist eine stark unerreichbare Kardinalzahl κ, in welcher die Menge der regulären Kardinalzahlen stationär ist. Da die Menge der starken Limeskardinalzahlen in κ abgeschlossen unbeschränkt ist, ist dann auch die Menge der unerreichbaren Kardinalzahlen stationär in κ. Da κ regulär ist, folgt daraus, dass κ die κ-te unerreichbare Kardinalzahl ist.

• Schwach kompakte Kardinalzahl
• Messbare Kardinalzahl
• Woodin-Kardinalzahl
• Stark kompakte Kardinalzahl
• Superkompakte Kardinalzahl

Literatur

• Thomas Jech: Set Theory, The Third Millennium Edition, Revised and Expanded; Springer-Verlag, ISBN 3540440852