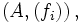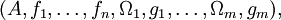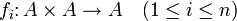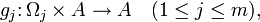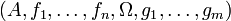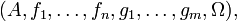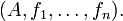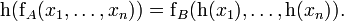- Universelle Algebra
-
Der Begriff algebraische Struktur, missverständlich auch „universelle Algebra“, „allgemeine Algebra“ oder „Algebra“ genannt, bezeichnet ein mathematisches Objekt.
Das Synonym allgemeine Algebra bezeichnet gleichzeitig auch den Teilbereich der Mathematik, der sich allgemein mit diesen Objekten beschäftigt. Es ist wiederum ein Teilbereich der Algebra (ohne Namenszusätze), dem grundlegenden und weitläufigen Teilbereich der Mathematik, in dem generell die Eigenschaften mathematischer Objekte im Zusammenhang mit auf ihnen erklärten Verknüpfungen behandelt werden. Die allgemeine Algebra ist zu unterscheiden von der abstrakten Algebra, einem anderen Teilbereich der Algebra, in dem spezielle algebraische Strukturen in abstrakter Form beschrieben (Gruppen, Ringe usw.) und auf ihre Eigenschaften untersucht werden. Die allgemeine Algebra setzt eine Abstraktionsebene über der abstrakten Algebra an und beschreibt sämtliche algebraischen Strukturen in einheitlicher, abstrakter Form („allgemein“) und untersucht deren Eigenschaften.
Da es auch noch eine spezielle algebraische Struktur innerhalb der abstrakten Algebra gibt, die wiederum den Namen Algebra (ohne Namenszusätze) trägt, ergibt sich insgesamt eine schwer überschaubare Begriffszuordnung. Angesichts dessen beugt im folgenden die Benennung des hier behandelten mathematischen Objektes als algebraische Struktur mit dem zugehörigen mathematischen Teilgebiet der allgemeinen Algebra Verwechslungen vor.
Inhaltsverzeichnis
Definition der algebraischen Struktur
Im Folgenden werden verschiedene Varianten der Definition einer algebraischen Struktur bzw. allgemeinen Algebra angegeben. Für allgemeine Algebra wird dabei generell auch kurz Algebra geschrieben, falls Missverständnisse ausgeschlossen sind. In der Literatur finden sich alle diese Varianten (und noch weitere), ohne dass bisher eine davon sich als etablierter als die anderen herauskristallisiert hätte oder gar als allgemein verbindlich akzeptiert worden wäre. Vielmehr werden sie je nach Bedarf gewählt und angepasst, so dass sie dem Abstraktionsgrad und der jeweils verwendeten Terminologie innerhalb einer abgeschlossenen Ausarbeitung entsprechen.
Variante 1
Die Variante 1 der Definition einer algebraischen Struktur ist eng verwandt mit der Definition einer Struktur in der Modelltheorie und mathematischen Logik.
Eine algebraische Struktur oder allgemeine Algebra ist ein Paar
bestehend aus einer nichtleeren Menge
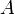 , der Trägermenge der Algebra, und einer Familie
, der Trägermenge der Algebra, und einer Familie 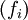 von (endlichstelligen) Verknüpfungen, auch fundamentale Operationen genannt, auf A.
von (endlichstelligen) Verknüpfungen, auch fundamentale Operationen genannt, auf A.Eine n-stellige Verknüpfung auf A ist eine Funktion
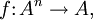 die n Elemente
die n Elemente 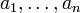 aus A immer auf ein (eindeutig bestimmtes) Element b aus A abbildet, b ist dann das Bild von
aus A immer auf ein (eindeutig bestimmtes) Element b aus A abbildet, b ist dann das Bild von 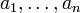 (Schreibweise:
(Schreibweise: 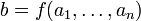 ). Ein Element aus A kann als eine nullstellige Verknüpfung, auch Konstante genannt, interpretiert werden, besondere Elemente werden meist mit einem speziellen Symbol (z. B. einem Buchstaben oder einer Zahl wie
). Ein Element aus A kann als eine nullstellige Verknüpfung, auch Konstante genannt, interpretiert werden, besondere Elemente werden meist mit einem speziellen Symbol (z. B. einem Buchstaben oder einer Zahl wie  , 0, 1) bezeichnet. Eine einstellige Verknüpfung ist eine Funktion von A nach A, die oft durch ein Symbol bezeichnet wird, das unmittelbar (d. h. ohne zusätzliche Klammern oder Trennzeichen) vor, hinter, über etc. das Element (Argument) geschrieben wird.
, 0, 1) bezeichnet. Eine einstellige Verknüpfung ist eine Funktion von A nach A, die oft durch ein Symbol bezeichnet wird, das unmittelbar (d. h. ohne zusätzliche Klammern oder Trennzeichen) vor, hinter, über etc. das Element (Argument) geschrieben wird.- Beispiel:
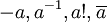
Beim Bild einer zweistelligen Verknüpfung wird in der Regel das Verknüpfungssymbol zur Vereinfachung zwischen die beiden Argumente geschrieben.
- Beispiel:
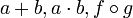 an Stelle von
an Stelle von 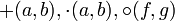
Meistens hat eine Algebra nur endlich viele Verknüpfungen
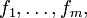 man schreibt dann für die Algebra einfach nur
man schreibt dann für die Algebra einfach nur 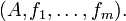
Der Typ oder die Signatur einer Algebra beschreibt die Stelligkeiten der Verknüpfungen. So wird zum Beispiel eine Gruppe meist als Struktur
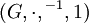 aufgefasst, wobei G die Grundmenge ist,
aufgefasst, wobei G die Grundmenge ist,  eine Funktion von
eine Funktion von 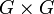 nach G (also eine zweistellige Funktion), − 1 eine einstellige Funktion von G nach G und 1 eine Konstante aus G. Abkürzend schreibt man: Der Typ einer Gruppe ist (2,1,0).
nach G (also eine zweistellige Funktion), − 1 eine einstellige Funktion von G nach G und 1 eine Konstante aus G. Abkürzend schreibt man: Der Typ einer Gruppe ist (2,1,0).Bemerkungen zu Variante 1
- Jede nichtleere Menge A lässt sich zu einer trivialen Algebra
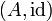 machen mit der identischen Abbildung
machen mit der identischen Abbildung 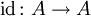 ,
, 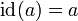 für alle
für alle 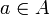 . Ebenso kann (A) als eine Algebra mit einer leeren Familie von Verknüpfungen aufgefasst werden.
. Ebenso kann (A) als eine Algebra mit einer leeren Familie von Verknüpfungen aufgefasst werden. - Manchmal erweist es sich auch als zweckmäßig, die leere Menge
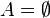 als Trägermenge einer Algebra zuzulassen, etwa damit sichergestellt ist, dass die Menge aller Unteralgebren (siehe unten) einer Algebra einen algebraischen Verband bildet.
als Trägermenge einer Algebra zuzulassen, etwa damit sichergestellt ist, dass die Menge aller Unteralgebren (siehe unten) einer Algebra einen algebraischen Verband bildet. - Man könnte sogar „unendlichstellige Algebren“ mit unendlichstelligen Operationen zulassen (z. B. σ-Algebren), dies würde jedoch dem üblichen Verständnis von „algebraisch“ widersprechen.[1]
- Eine Verallgemeinerung allgemeiner (vollständiger) Algebren sind partielle Algebren, bei welchen nicht nur totale Funktionen sondern auch partielle Funktionen als Verknüpfung zugelassen sind.[2] Z. B. sind Körper (K,+,0,-,·,1,−1) streng genommen keine vollständigen Algebren, weil −1 nur auf K\{0} definiert ist.
Variante 2
Seien
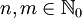 (natürliche Zahlen mit 0). Ein Tupel
(natürliche Zahlen mit 0). Ein Tupelbestehend aus nichtleeren Mengen
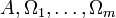 , inneren Verknüpfungen
, inneren Verknüpfungen 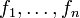 und äußeren Verknüpfungen
und äußeren Verknüpfungen 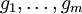 der Form
der Formund
heißt algebraische Struktur oder allgemeine Algebra. A wird die Träger- oder Grundmenge der Algebra und
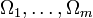 werden die Operatorenbereiche der äußeren Verknüpfungen genannt.[3]
werden die Operatorenbereiche der äußeren Verknüpfungen genannt.[3]Sind alle Operatorenbereiche gleich
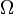 , so schreibt man kürzer
, so schreibt man kürzeroder
und bei m = 0 auch nur
Das m + 2-Tupel
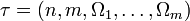 bzw. das Tripel τ = (n,m,Ω) heißt der Typ der Algebra, im Falle m = 0 schreibt man einfach τ = (n).
bzw. das Tripel τ = (n,m,Ω) heißt der Typ der Algebra, im Falle m = 0 schreibt man einfach τ = (n).Bemerkungen zu Variante 2
- Die Anzahl der Verknüpfungen ist hier als endlich beschrieben, gelegentlich werden aber auch unendliche Anzahlen von Verknüpfungen betrachtet.
- n = 0 sowie m = 0 sind ausdrücklich zugelassen. Die „leere“ algebraische Struktur (n = m = 0) ist dann (A), die Trägermenge ohne innere oder äußere Verknüpfungen.
- Für jede äußere Verknüpfung
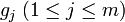 kann eine Familie
kann eine Familie 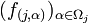 von einstelligen inneren Verknüpfungen
von einstelligen inneren Verknüpfungen 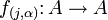 definiert werden mit
definiert werden mit 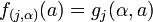 für alle
für alle 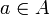 . Umgekehrt ist durch jede solche Familie
. Umgekehrt ist durch jede solche Familie 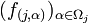 von einstelligen inneren Verknüpfungen auch wieder eine entsprechende äußere Verknüpfung
von einstelligen inneren Verknüpfungen auch wieder eine entsprechende äußere Verknüpfung 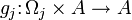 gegeben. Deshalb kann eine algebraische Struktur nach Variante 2
gegeben. Deshalb kann eine algebraische Struktur nach Variante 2 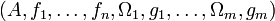 auch aufgefasst werden als eine algebraische Struktur nach Variante 1
auch aufgefasst werden als eine algebraische Struktur nach Variante 1 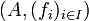 , mit der Indexmenge
, mit der Indexmenge 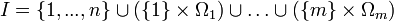 .[1]
.[1]
Beispiele zu Variante 2
- Ein üblicher
 -Vektorraum V hätte die algebraische Struktur
-Vektorraum V hätte die algebraische Struktur 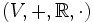 , wobei
, wobei  die Multiplikation von Vektoren (üblicherweise von Links) mit Skalaren bezeichnet.
die Multiplikation von Vektoren (üblicherweise von Links) mit Skalaren bezeichnet.
- Eine beliebige Menge X, auf der eine Gruppe G operiert, hätte die algebraische Struktur
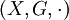 , wobei
, wobei  die Operation der Gruppe auf X symbolisiert.
die Operation der Gruppe auf X symbolisiert.
Spezifizierung algebraischer Strukturen
Nachdem die Verknüpfungen angegeben sind, spezifiziert man die Natur der Algebra näher durch Axiome, die in der abstrakten Algebra (Teilgebiet der Mathematik) meist in Form von Gleichungen geschrieben werden und gegebene Eigenschaften der Verknüpfungen festlegen. Ein Beispiel ist das Assoziativgesetz für eine zweistellige Verknüpfung:
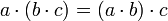 für alle Elemente
für alle Elemente 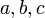 aus A.
aus A.
Unterstrukturen (Unteralgebren)
Ist A die Grundmenge einer algebraischen Struktur, so kann man mit Hilfe der Verknüpfungen von A auf einer Teilmenge
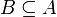 von A eine neue algebraische Struktur des gleichen Typs definieren, falls die Menge B so gewählt ist, dass die Verknüpfungen der ursprünglichen Struktur nicht aus der Menge B herausführen. Das bedeutet, wenn man die Verknüpfungen der ursprünglichen algebraischen Struktur auf die Elemente von B anwendet, dürfen keine Elemente entstehen, die nicht in B sind – insbesondere müssen die Konstanten bereits in B enthalten sein. In der konkreten Anwendung sind z. B. Untergruppen die Unterstrukturen einer Gruppe. Je nachdem, wie man die Gleichungen zur Definition der algebraischen Struktur gewählt hat, können die Unterstrukturen aber ganz verschieden aussehen. So lassen sich z. B. Gruppen so definieren, dass die Unterstrukturen Normalteiler sind.
von A eine neue algebraische Struktur des gleichen Typs definieren, falls die Menge B so gewählt ist, dass die Verknüpfungen der ursprünglichen Struktur nicht aus der Menge B herausführen. Das bedeutet, wenn man die Verknüpfungen der ursprünglichen algebraischen Struktur auf die Elemente von B anwendet, dürfen keine Elemente entstehen, die nicht in B sind – insbesondere müssen die Konstanten bereits in B enthalten sein. In der konkreten Anwendung sind z. B. Untergruppen die Unterstrukturen einer Gruppe. Je nachdem, wie man die Gleichungen zur Definition der algebraischen Struktur gewählt hat, können die Unterstrukturen aber ganz verschieden aussehen. So lassen sich z. B. Gruppen so definieren, dass die Unterstrukturen Normalteiler sind.Homomorphismen
Strukturtreue Abbildungen, sogenannte Homomorphismen, zwischen je zwei algebraischen Strukturen A und B vom selben Typ (sie haben also Verknüpfungen von jeweils gleichen Stelligkeiten und gegebenen spezifischen Eigenschaften) sind mit den Verknüpfungen der beiden algebraischen Strukturen „verträglich“. Jede algebraische Struktur hat deshalb ihren eigenen Homomorphismus-Begriff und definiert daher eine Kategorie.
Einander entsprechende Verknüpfungen in A und B werden meist mit dem gleichen Symbol bezeichnet. So wird etwa in jeder betrachteten Gruppe die Gruppenoperation einheitlich als
 geschrieben. Müssen im Einzelfall die beiden Verknüpfungen auseinandergehalten werden, werden in der Regel die Symbole ihrer Grundmengen oder ähnliches als Indizes beigefügt, also z. B.
geschrieben. Müssen im Einzelfall die beiden Verknüpfungen auseinandergehalten werden, werden in der Regel die Symbole ihrer Grundmengen oder ähnliches als Indizes beigefügt, also z. B. 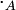 und
und 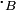 . Ein Homomorphismus
. Ein Homomorphismus 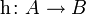 ist eine Funktion, die für jede Verknüpfung
ist eine Funktion, die für jede Verknüpfung 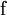 (mit der Stelligkeit n) die folgende Bedingung erfüllt:
(mit der Stelligkeit n) die folgende Bedingung erfüllt:Die besonderen Schreibweisen, der null-, ein- und zweistelligen Verknüpfungen werden berücksichtigt:
- Ist e eine Konstante (0-stellige Verknüpfung), dann ist
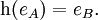
- Ist
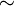 eine einstellige Verknüpfung, dann ist
eine einstellige Verknüpfung, dann ist 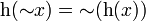 – meist einfach
– meist einfach 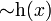 geschrieben, wenn im Kontext nicht noch ein spezielles Symbol
geschrieben, wenn im Kontext nicht noch ein spezielles Symbol 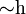 existiert. Wird die Verknüpfung nicht links an das Argument geschrieben (sondern rechts davon, drunter, drüber usw.), ergibt sich dieses Problem ohnehin nicht. Z. B. wird
existiert. Wird die Verknüpfung nicht links an das Argument geschrieben (sondern rechts davon, drunter, drüber usw.), ergibt sich dieses Problem ohnehin nicht. Z. B. wird ![\widehat{\operatorname h(x)}\ \left[ =\widehat{\ }(\operatorname h(x))\right]](/pictures/dewiki/49/14afce478952037c7c13ae5c774e31df.png) streng von einem möglichen
streng von einem möglichen ![\widehat{\operatorname h}(x)\ \left[ =(\widehat{\operatorname h})(x)\right]](/pictures/dewiki/54/61f4b33c0649a9a63aa6e256e9261366.png) unterschieden. Ebenso verhält es sich mit den Ausdrücken
unterschieden. Ebenso verhält es sich mit den Ausdrücken ![h(x)^{{-}1}\ \left[ =(h(x))^{{-}1}\right]\,\!](/pictures/dewiki/100/d2899509b09b3d2f18f0c23bac083c57.png) und
und ![h^{{-}1}(x)\ \left[ =(h^{{-}1})(x)\right]\,\!.](/pictures/dewiki/50/277234142be72113e0d66c377ba2fdd4.png)
- Ist
 eine zweistellige Verknüpfung, dann ist
eine zweistellige Verknüpfung, dann ist 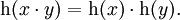
Ein surjektiver Homomorphismus wird Epimorphismus genannt, ein injektiver Monomorphismus. Ein Homomorphismus von A in sich (also falls B = A gilt) heißt Endomorphismus. Ein bijektiver Homomorphismus, dessen Umkehrfunktion ebenfalls ein Homomorphismus ist, heißt Isomorphismus. Ist der Isomorphismus gleichzeitig auch Endomorphismus, so heißt er Automorphismus.
Siehe auch: Homomorphiesatz.
Kongruenzrelationen
Auf algebraischen Strukturen lassen sich spezielle Typen von Äquivalenzrelationen finden, die mit den Verknüpfungen einer algebraischen Struktur verträglich sind. Diese werden dann Kongruenzrelationen genannt. Mit Hilfe von Kongruenzrelationen lassen sich Faktoralgebren bilden, d. h. es wird aus der ursprünglichen algebraischen Struktur eine Struktur gleichen Typs erzeugt, deren Elemente allerdings dann die Äquivalenzklassen bezüglich der Kongruenzrelation sind. Die Verknüpfungen sind aufgrund der speziellen Eigenschaften der Kongruenzrelation wohldefiniert. In vielen konkreten Anwendungen entsprechen die Äquivalenzklassen den Neben- bzw. Kongruenzklassen bestimmter Unterstrukturen z. B. Normalteilern bei Gruppen oder Idealen bei Ringen usw.
Produkte
Bildet man das mengentheoretische direkte Produkt der Grundmengen mehrerer allgemeiner Algebren des gleichen Typs, so kann man wiederum eine neue Algebra gleichen Typs auf dieser Produktmenge erhalten, indem man die neuen Verknüpfungen dieser Algebra komponentenweise durch die Verknüpfungen der ursprünglichen Algebren definiert. Diese kann allerdings andere Eigenschaften haben, als die ursprüngliche Algebra; z. B. muss das Produkt von Körpern nicht mehr ein Körper sein.
„Zoo” der algebraischen Strukturen
Beispiel: Gruppen
Um zu sehen, wie das funktioniert, betrachten wir die Definition einer Gruppe. Üblicherweise ist eine Gruppe definiert als eine Menge A mit einer zweistelligen Verknüpfung *, wobei die folgenden drei Axiome erfüllt sind:
- x * (y * z) = (x * y) * z (Assoziativität)
- es gibt ein e so dass e * x = x = x * e (neutrales Element)
- für jedes x gibt es ein i so dass x * i = e = i * x (inverses Element)
(Manchmal findet man noch die Forderung der „Abgeschlossenheit“, dass x * y wieder in A liegen soll, aber aus der Sicht eines Algebraikers beinhaltet der Begriff der „zweistelligen Verknüpfung“ diese Eigenschaft bereits.)
Diese Definition hat aber die Eigenschaft, dass die Axiome nicht allein durch Gleichungen ausgedrückt werden, sondern auch den Quantor „es gibt … so dass“ enthalten; in der allgemeinen Algebra versucht man deshalb solche Axiome zu vermeiden. Die Vereinfachung der Axiome auf eine reine Gleichungsform ist hier nicht schwierig: Wir fügen eine 0-stellige Verknüpfung e und eine einstellige Verknüpfung „−1“ hinzu und definieren eine Gruppe als eine Menge A mit einer zweistelligen Verknüpfung *, einem Element e und einer einstelligen Verknüpfung „−1“, die den folgenden Axiomen genügt:
- x * (y * z) = (x * y) * z
- e * x = x = x * e
- x * (x−1) = e = (x−1) * x
Es ist nun wichtig zu prüfen, ob damit tatsächlich die Definition einer Gruppe erreicht wurde. Es könnte ja sein, dass dadurch noch nicht alle Eigenschaften einer Gruppe gegeben sind oder gar zuviele. Nichts in der Definition der Gruppe besagt zum Beispiel, dass das neutrale Element eindeutig ist, und wenn es ein zweites neutrales Element e' gäbe, welches der beiden sollte dann der Wert der 0-stelligen Verknüpfung e sein? Dies ist jedoch hier kein Problem, da das neutrale Element stets eindeutig bestimmt ist, und dasselbe gilt auch für das inverse Element jedes x. Tatsächlich stimmen die beiden Definitionen einer Gruppe überein.
Arten von Algebraischen Strukturen
In der folgenden Liste werden alle (2-stelligen) Verknüpfungen, neutrale Elemente (= 0-stellige Verknüpfungen), Inversenabbildungen (= 1-stellige Verknüpfungen) und Operatorbereiche angegeben.
Im normalen Gebrauch gibt man dagegen für algebraische Strukturen nur die zweistelligen Verknüpfungen und die Operatorbereiche an (manchmal noch die neutralen Elemente), für alle anderen gibt es meist Standardnotationen.
Eine nicht vollständige Liste verschiedener algebraischer Strukturen:
- Gruppoid oder Magma, auch Binar oder Operativ (O,*): eine nichtleere Menge O mit einer zweistelligen Verknüpfung *.
- Quasigruppe (Q,*): ein Gruppoid in dem zu je zwei Elementen a, b die Gleichungen a*x=b und y*a=b stets eindeutige Lösungen x, y in Q besitzen (x und y können verschieden sein). Äquivalent dazu: eine Equasigruppe (siehe unten).
- Loop (L,*,1): eine Quasigruppe mit einem neutralen Element 1.
- Halbgruppe (S,*): ein assoziatives Gruppoid.
- Band (B,*): eine idempotente Halbgruppe.
- Halbverband (H,*): eine kommutative Band.
- Monoid (M,*,1): eine Halbgruppe mit einem neutralen Element 1.
- Gruppe (G,*,1,−1): ein Monoid mit einem inversen Element a−1 zu jedem Element a – oder äquivalent dazu: eine assoziative Quasigruppe oder eine assoziative Loop.
- Abelsche Gruppe (G,+,0,-): eine kommutative Gruppe. Abelsche Gruppen werden meist additiv geschrieben, man spricht dann von einem Modul. Das neutrale Element eines Moduls wird mit 0 und das „Inverse“ eines Elements a als das Negative -a bezeichnet.
- Verband (V,
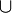 ,
, 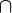 ): eine Menge V mit zwei Verknüpfungen
): eine Menge V mit zwei Verknüpfungen 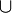 (z. B. Vereinigung) und
(z. B. Vereinigung) und 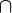 (z. B. Durchschnitt), so dass (V,
(z. B. Durchschnitt), so dass (V, 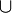 ) und (V,
) und (V, 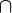 ) kommutative Halbgruppen sind und die Absorptionsgesetze erfüllt werden. (V,
) kommutative Halbgruppen sind und die Absorptionsgesetze erfüllt werden. (V, 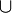 ) und (V,
) und (V, 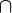 ) sind dann Halbverbände.
) sind dann Halbverbände. - Halbring (H,+,·): eine Menge H mit zwei Verknüpfungen + (Addition) und · (Multiplikation), mit denen (H,+) und (H,·) Halbgruppen sind und die Distributivgesetze erfüllt werden. Oft soll (H,+) aber auch noch kommutativ sein und/oder ein neutrales Element 0 besitzen, die Definitionen sind hier nicht einheitlich!
- Dioid (D,+,0,·,1): eine Menge D mit zwei Verknüpfungen + (Addition) und · (Multiplikation), so dass (D,+,0) und (D,·,1) Monoide sind und die Distributivgesetze erfüllt werden.
- Boolescher Verband oder Boolesche Algebra (B,
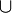 , 0,
, 0, 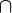 ,1,c): ein Dioid, der ein Verband (B,
,1,c): ein Dioid, der ein Verband (B, 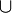 ,
, 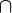 ) ist mit einem Komplement ac zu jedem Element a.
) ist mit einem Komplement ac zu jedem Element a. - Ring (R,+,0,-,·): ein Halbring, so dass (R,+,0,-) eine abelsche Gruppe ist.
- Unitärer Ring (R,+,0,-,·,1): ein Ring mit neutralem Element 1 für die Multiplikation.
- Integritätsring oder Integritätsbereich (I,+,0,-,·,1): ein unitärer, kommutativer Ring mit 0
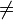 1, für den
1, für den 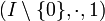 ein (kürzbares) Monoid ist.
ein (kürzbares) Monoid ist. - Schiefkörper (K,+,0,-,·,1,−1): ein Ring, bei dem (K\{0},·,1,−1) eine Gruppe ist.
- Körper (K,+,0,-,·,1,−1): ein Schiefkörper, der kommutativ ist.
- Equasigruppe (E,*,\,/): ein Gruppoid mit zwei weiteren Verknüpfungen \ (Linksdivision) und / (Rechtsdivision), so dass für je zwei Elemente a, b gilt: a*(a\b) = b und (b/a)*a = b. D.h. zu je zwei Elementen existieren stets ein eindeutiger Links- und ein eindeutiger Rechtsquotient (diese können verschieden sein). Äquivalent dazu: eine Quasigruppe.
- Multiplikativer Verband oder kurz m-Verband, auch Verbandsgruppoid, verbandsgeordnetes Gruppoid oder kurz l-Gruppoid (engl.: lattice = Verband) (L,
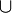 ,
, 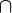 , ·): ein Verband (L,
, ·): ein Verband (L, 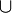 ,
, 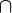 ) mit einer weiteren Verknüpfung · (Multiplikation), so dass die Distributivgesetze mit
) mit einer weiteren Verknüpfung · (Multiplikation), so dass die Distributivgesetze mit 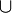 als Addition erfüllt werden.
als Addition erfüllt werden. - Modul (M,+,0,-,·,R) über einem Ring R (zur Vereinfachung werden die Ring-Verknüpfungen nicht aufgeführt), kurz: R-Modul: Eine abelsche Gruppe (M,+,0,-) mit einem Ring R und einer äußeren Verknüpfung ·: R×M -> M (Skalarmultiplikation), die assoziativ ist und die Distributivgesetze erfüllt.
- K-Vektorraum (V,+,0,-,·,K): ein Modul über einem Körper K.
- K-Algebra (A,+,0,-,·,*,K): Ein K-Vektorraum (oder -Modul) mit einer bilinearen Verknüpfung * („Vektormultiplikation“), die die Distributivgesetze erfüllt und assoziativ mit der Skalarmultiplikation ist (sie muss nicht selbst assoziativ sein!).
- Assoziative Algebra (A,+,0,-,·,*,K): eine K-Algebra, deren Multiplikation assoziativ ist.
Für eine ausführlichere Übersicht siehe Hierarchie mathematischer Strukturen.
Mischstrukturen
Algebraische Strukturen können gleichzeitig auch nicht-algebraische Strukturen sein, wie z. B. topologische Räume. Eine topologische Gruppe ist ein topologischer Raum mit einer Gruppenstruktur, so dass die Operationen Multiplikation und Inversenbildung stetig sind. Eine topologische Gruppe hat sowohl eine topologische, als auch eine algebraische Struktur. Andere häufige Beispiele sind topologische Vektorräume und Lie-Gruppen.
Ausblick
Dieser Artikel reicht nicht aus, die Vielfalt der Ergebnisse der allgemeinen Algebra zu zeigen. Die Motivation der allgemeinen Algebra ist die große Anzahl verschiedener Algebren (im Sinne der allgemeinen Algebra), wie z. B. Gruppen, Monoide, Verbände, die aber alle ähnliche Theoreme zulassen. Vor der Entwicklung der allgemeinen Algebra wurden viele Theoreme (vor allen die Isomorphiesätze) für jede Struktur einzeln bewiesen, aber nun kann man sie ein einziges Mal für alle Arten algebraischer Strukturen beweisen.
Eine noch allgemeinere Idee liegt der Kategorientheorie zugrunde. Sie ist auf viele Situationen anwendbar, die in universeller Algebra nicht darstellbar sind (etwa topologische Sachverhalte), und liefert so weiter reichende Aussagen. Umgekehrt lassen sich manche Aussagen der allgemeinen Algebra nicht auf alle Kategorien übertragen. So sind also beide Teilgebiete nützlich. Die Verbindung zwischen ihnen ist diese: Für vorgegebene Verknüpfungen und Axiome bilden die zugehörigen Algebren und Homomorphismen eine Kategorie.
Einzelnachweise
Literatur
- G. Birkhoff: Lattice Theory. 3rd Edition. AMS, Providence, RI 1973, ISBN 0-8218-1025-1.
- Stanley Burris, H.P. Sankappanavar: A Course in Universal Algebra. Springer-Verlag, New York 1981, ISBN 3-540-90578-2.
- P. M. Cohn: Universal Algebra. Harper & Row, New York 1965.
- H. Ehrig, B. Mahr, F. Cornelius, M. Grosse-Rhode, P. Zeitz: Mathematisch-strukturelle Grundlagen der Informatik. Springer-Verlag, Berlin et al. 2001, ISBN 3-540-41923-3.
- Roger Godement: Algebra. Hermann, Paris 1968.
- G. Grätzer: Universal Algebra. D. Van Nostrant Co., Inc., Princeton (NJ) et al 1968.
- Pierre Antoine Grillet: Abstract Algebra. 2nd Ed.. Springer Science + Business Media, New York 2007, ISBN 978-0-387-71567-4.
- Th. Ihringer: Allgemeine Algebra. Heldermann Verlag, Lemgo 2003, ISBN 3-88538-110-9.
- N. Jacobson: Basic Algebra I/II. W. H. Freeman, San Francisco 1980, ISBN 0-7167-1480-9/ISBN 0-7167-1933-9.
- K. Meyberg: Algebra, Teil 1/2. Carl Hanser Verlag, München 1975/76, ISBN 3-446-11965-5/ISBN 3-446-12172-2.
- B.L. van der Waerden: Algebra I/II. Springer-Verlag, Berlin-Heidelberg-New York 1971 und 1967, ISBN 3-540-03561-3/ISBN 3-540-03869-8.
- H. Werner: Einführung in die allgemeine Algebra. Bibliographisches Institut, Mannheim 1978, ISBN 3-411-00120-8.
- Jorge Martinez: Ordered Algebraic Structures. Springer, 2002, ISBN 1402007523.
Wikimedia Foundation.