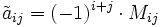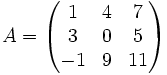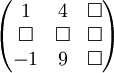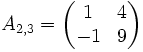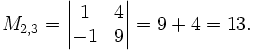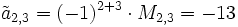Unterdeterminante

Minor oder Unterdeterminante ist ein Begriff aus dem mathematischen Teilgebiet der linearen Algebra. Man bezeichnet damit die Determinante einer quadratischen Untermatrix, die durch Streichen einer oder mehrerer Spalten und Zeilen einer Matrix entsteht. Die Anzahl der Zeilen bzw. Spalten der entsprechenden Untermatrix gibt die Ordnung des Minors an.

Cofaktoren

Zu einer quadratischen $n \times n$-Matrix lassen sich die Cofaktoren 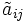$\tilde a_{ij}$ gemäß folgender Formel berechnen:^[1]

$\tilde a_{ij} = (-1)^{i+j} \cdot M_{ij}$

Dabei ist M_ij der Minor (n − 1)-ter Ordnung, der aus derjenigen Untermatrix berechnet wird, die durch Streichen der i-ten Zeile und j-ten Spalte entsteht.

Aus den Cofaktoren lässt sich wieder eine Matrix bilden, deren Transponierte als Adjunkte oder komplementäre Matrix bezeichnet wird. Mit ihr kann man die Inverse einer Matrix berechnen. Der Laplace'sche Entwicklungssatz verwendet die Cofaktoren einer Matrix zur Berechnung ihrer Determinante.

Beispiel

Es soll der Minor M_2,3 und der Cofaktor 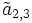$\tilde a_{2,3}$ der folgenden Matrix bestimmt werden:

$A = \begin{pmatrix} 1 & 4 & 7 \\ 3 & 0 & 5 \\ -1 & 9 &11 \end{pmatrix}$

Durch Streichen der zweiten Zeile und dritten Spalte

$\begin{pmatrix} 1 & 4 & \Box \\ \Box & \Box & \Box \\ -1 & 9 & \Box \end{pmatrix}$

entsteht die Matrix

$A_{2,3} = \begin{pmatrix} 1 & 4 \\ -1 & 9 \end{pmatrix}$

Daraus lässt sich der Minor M_2,3 berechnen.

$M_{2,3} = \begin{vmatrix} 1 & 4 \\ -1 & 9 \end{vmatrix} = 9 + 4 = 13.$

Für den Cofaktor 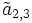$\tilde a_{2,3}$ gilt

$\tilde a_{2,3} = (-1)^{2+3} \cdot M_{2,3} = -13$

Hauptminoren

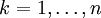Es sei A eine $n\times n$-Matrix und für $k=1,\ldots,n$ sei A_k die linke obere 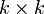$k\times k$-Teilmatrix von A, die durch Streichung der n − k am weitesten rechts gelegenen Spalten und n − k untersten Zeilen entsteht. Die Determinante von A_k heißt k-ter Hauptminor (oder Hauptunterdeterminante / Hauptabschnittsdeterminante).

Die Hauptminoren haben eine Bedeutung für die Feststellung der Definitheit symmetrischer bzw. hermitescher Matrizen; für das Hauptminorenkriterium siehe Definitheit von Hauptminoren.

Einzelnachweis

1. ↑ Siegfried Bosch: Lineare Algebra. Springer, 2001, ISBN 3-540-41853-9, S. 148

Literatur

• Wolfgang Gawronski: Grundlagen der Linearen Algebra. Aula-Verlag, Wiesbaden 1996, ISBN 3-89104-566-2, S. 193