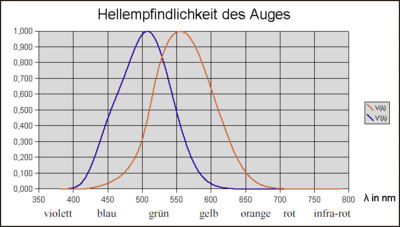
- V(lambda)-Kurve
-
Hellempfindlichkeitskurve für Nacht-(blau) und Tagsehen (rot).Die Hellempfindlichkeitskurve V(λ) beschreibt den spektralen Hell-Empfindlichkeitsgrad von Testpersonen bei Tageslicht (photopischer Bereich). Sie wurde empirisch ermittelt und 1924 im „Internationalen Standard Beobachter“ veröffentlicht (Internationale Beleuchtungskommission, Commission Internationale de l'Éclairage, CIE) und 1982 überarbeitet (CIPM Comité International des Poids et Mesures). In Deutschland ist sie unter DIN 5031 normiert. Die spezifische Empfindlichkeit in verschiedenen Wellenbereichen des sichtbaren Lichts ist Grundlage der Photometrie und stellt den Zusammenhang her zwischen Einheiten der Strahlungs- und Lichtstärke. Die so genannte Veq(λ)-Kurve für das Dämmerungssehen (mesopischer Bereich) und die V'(λ))-Kurve für das Nachtsehen (skotopischer Bereich) sind für die Lichttechnik nur in Ausnahmefällen von Bedeutung.
Die spektrale Verschiebung zwischen Tag- und Nachtsehen wird als Purkinje-Effekt bezeichnet.
Absorptionsspektrum von Chlorophyll a und b.Die Sehempfindlichkeit des Menschen (und vieler anderer Säuger und Vögel) hat sich evolutionär entwickelt in einer von Pflanzen geprägten, grünen Umgebung. Es war daher von Vorteil, in dem Spektralbereich sehempfindlich zu sein, der vom reflektierten bzw. absorbierten Licht der Pflanzen übrig gelassen wurde.
Siehe auch
Weblinks
Wikimedia Foundation.
