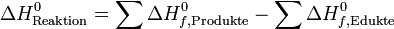Verdampfungsenthalpie

Die Enthalpie ist ein Maß für die Energie eines thermodynamischen Systems. Sie wird in der Regel durch den Buchstaben H (Einheit: Joule, J) symbolisiert, wobei das H vom englischen heat content (Wärmeinhalt) abgeleitet ist. In der Chemie und Technik spielen außerdem die molare Enthalpie H_m (Einheit: kJ/mol) und die spezifische Enthalpie h (Einheit: kJ/kg) eine wichtige Rolle. Sie beschreiben die Enthalpie in Bezug auf die Stoffmenge n bzw. die Masse m.

Die Enthalpie ist die Legendre-Transformierte der inneren Energie bezüglich des Volumens. Sie ist das thermodynamische Potential im SpN-Ensemble.

Allgemein

Die Enthalpie setzt sich additiv aus zwei Teilen zusammen, der inneren Energie U und der Volumenarbeit pV:

H = U + pV,

Die innere Energie besteht aus der thermischen Energie - beruhend auf der ungerichteten Bewegung der Moleküle (Kinetische Energie, Rotationsenergie, Schwingungsenergie) - der chemischen Bindungsenergie und der Potentiellen Energie der Atomkerne. Hinzu kommen Wechselwirkungen mit elektrischen und magnetischen Dipolen. Sie nimmt ungefähr proportional zur Temperatur des Systems zu und ist am absoluten Nullpunkt gleich der Nullpunktsenergie. Die Volumenarbeit ist in diesem Fall anschaulich die Arbeit, die gegen den Druck p verrichtet werden muss, um das Volumen V zu erzeugen, das vom System im betrachteten Zustand eingenommen wird (ΔV = V).

Differenziell ausgedrückt wird aus H = U + pV

$\mathrm dH = \mathrm dU + d(p \cdot V) = T \cdot dS - p \cdot dV + p \cdot dV + V \cdot dp = T \cdot dS + V \cdot dp$.

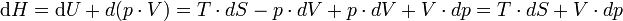(Man beachte den Unterschied zwischen „steil“ und kursiv gedruckten Differentialen, d versus d: erstere sollen für Zustandsgrößen vorbehalten bleiben.)

Standardbildungsenthalpie

Die Standardbildungsenthalpie ist die Enthalpie, die bei der Bildung von einem Mol einer Substanz aus der allotropisch stabilsten Form der reinen Elemente unter Standardbedingungen (1,013 bar und 25 °C) frei wird (exotherme Reaktion, negatives Vorzeichen) oder zur Bildung erforderlich ist (endotherme Reaktion, positives Vorzeichen). Sie wird in Kilojoule pro Mol angegeben und symbolisch mit 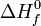$\Delta H_f^0$ bezeichnet (f von engl. formation, Bildung; der Exponent Null steht für Standardbedingungen).

Ist sie negativ, so wird bei der Bildung der Substanz aus den Elementen Energie frei, ist sie dagegen positiv, so muss Energie zur Bildung der Substanz aus ihren Ausgangselementen aufgewendet werden. Stark negative Werte der Standardbildungsenthalpie sind ein Kennzeichen chemisch besonders stabiler Verbindungen (d. h. bei ihrer Bildung wird viel Energie frei und zur Zerstörung der Bindungen muss auch wieder viel Energie aufgewendet werden). Die Standardbildungsenthalpie der chemischen Elemente in ihrem stabilsten Zustand (H₂, He, Li, ...) ist per Definition auf 0 kJ/mol festgesetzt.

Eine wichtige Anwendung der Standardbildungsenthalpien ist, dass sich damit Reaktionsenthalpien durch den Satz von Hess berechnen lassen: So ist die Reaktionsenthalpie einer gegebenen Reaktion unter Standardbedingungen die Differenz zwischen den Standardbildungsenthalpien der Reaktionsprodukte ("Produkte") einerseits und der Ausgangsstoffe (Reaktanden; "Edukte") andererseits. Symbolisch lässt sich dies durch die folgende Formel wiedergeben:

$\Delta H_{\mathrm{Reaktion}}^0=\sum \Delta H_{f,\mathrm{Produkte}}^{0} -\sum \Delta H_{f, \mathrm{Edukte}}^{0}$

Dies ist gleichbedeutend mit der Aussage, dass die Bildungsenthalpie eines Stoffes unter Normalbedingungen nur vom Stoff selbst, und nicht von dem Weg seiner Herstellung abhängt. Die Bildungsenthalpie ist also eine thermodynamische Zustandsgröße. Alle Werte beziehen sich auf das thermodynamische Gleichgewicht, da sonst die Temperatur nicht definiert wäre.

Physikalische Bedeutung der Enthalpie (Thermodynamik)

Die Thermodynamik beschreibt im engeren Sinne nur die intermolekularen Kräfte, also die energetischen Beziehungen (Phasenzustände bzw. deren Änderungen) zwischen den einzelnen Molekülen eines Stoffs.

Verdampfungsenthalpie / Kondensationsenthalpie

Temperaturabhängigkeit der Verdampfungsenthalpie von Wasser, Methanol, Benzol und Aceton

Die Verdampfungsenthalpie Δ_VH ist die Energie, die erforderlich ist, um ein Mol einer Substanz isotherm und isobar vom flüssigen in den gasförmigen Zustand zu transportieren.

Die Verdampfungsenthalpie ist vom Stoff und vom Siedepunkt abhängig, wobei sie immer positiv ist und ihr Vorzeichen daher in der Regel nicht angegeben wird.

Kondensationsenthalpie Δ_KH ist demzufolge die Energie, die frei wird, wenn ein Mol einer Substanz kondensiert, wobei diese wieder isotherm und isobar vom gasförmigen in den flüssigen Aggregatzustand übergeht. Sie trägt immer ein negatives Vorzeichen.

In der Regel werden in Tabellenwerken Verdampfungsenthalpie-Daten entweder auf 25 °C oder den jeweiligen Siedepunkt bezogen, es gilt dabei immer Δ_VH = − Δ_KH.

Bei Gemischen oder Lösungen von Stoffen addieren sich die Enthalpien im Verhältnis ihrer Mischungsanteile.

Für nähere Erläuterungen siehe Verdampfungswärme

Sofern für eine Substanz keine Verdampfungsenthalpiewerte verfügbar sind, kann man diese aus deren Dampfdruckkurve gemäß Clausius-Clapeyron für beliebige Temperaturen einfach berechnen.

In seltenen Fällen wurden Werte für Verdampfungsenthalpien tabelliert. Die Verdampfungsenthalpie kann immer dann durch Differenzbildung aus den thermodynamischen Daten abgeleitet werden, wenn Standardbildungsenthalpie-Werte für den flüssigen und gasförmigen Aggregatzustand bekannt sind, z. B. für Wasser, Schwefelkohlenstoff, Methanol, Ethanol, Ameisensäure, Essigsäure, Brom in obenstehender Tabelle.

1. Kochsalz, Verdampfungsenthalpie = +170 kJ/mol (bei 1465 °C, Tabellenwert)
2. Zur praktischen Berechnung der Verdampfungswärme werden folgende Tabellenwerte für die Bildungsenthalpie verwendet:

NaCl (schmelze) $\longrightarrow$ NaCl (g)

-386 kJ/mol                   -182 kJ/mol           Bildungsenthalpien (25 °C)

$\rightarrow$ Verdampfungsenthalpie +204 kJ/mol

Anm.: Der Unterschied der zwei Werte 170 und 204 liegt im üblichen Rahmen. Die Verdampfungsenthalpie ist temperaturabhängig und nimmt ab in Richtung Siedepunkt, am kleinsten bei Erreichen des kritischen Temperaturpunkts.

Sublimationsenthalpie

Die Sublimation beschreibt den Übergang eines Feststoffs in die Gasphase unter Umgehung der flüssigen Schmelzphase (technische Anwendung bei der Gefriertrocknung). Die Sublimationsenthalpie wird teilweise in Tabellenwerken aufgeführt. Prinzipiell dürfen hierzu bei gleicher Bezugstemperatur auch Schmelz- und Verdampfungsenthalpie zusammengefasst werden.

Sublimationsenthalpie = Schmelzenthalpie + Verdampfungsenthalpie.

Die Sublimationsenthalpie kann immer dann aus den thermodynamischen Daten abgeleitet werden, wenn Standardbildungsenthalpie-Werte für den festen und gasförmigen Aggregatzustand bekannt sind, z. B. bei Kohlenstoff und Iod in obenstehender Tabelle

1. Sublimationsenthalpie Kochsalz: 211 kJ/mol (25 °C, Tabellenwert)

NaCl (s) $\longrightarrow$ NaCl (g)

-411 kJ/mol      -182 kJ/mol           Bildungsenthalpien (25 °C)

$\rightarrow$ Sublimationsenthalpie +229 kJ/mol

Anm.: Das Beispiel zeigt, dass man prinzipiell auch Vorgänge berechnen kann, die praktisch kaum durchführbar sind. Die "Sublimationsenthalpie von elementarem Kohlenstoff" wurde so "ermittelt".

Schmelzenthalpie / Kristallisationsenthalpie

Nach dem Erhitzen einer festen Substanz bis zu Ihrer Schmelzpunkttemperatur wird bei dieser Temperatur Schmelzwärme aufgenommen, ohne dass die Temperatur weiter ansteigt. Diese Form von Wärme wird latente Wärme genannt, weil diese keine Temperaturänderung bewirkt. Dabei wird das Kristallgitter zerstört. Bei ionischen Feststoffen entstehen bei der Phasenumwandlung fest/flüssig Salzschmelzen mit leicht beweglichen Ionen (techn. Anwendung bei der Schmelzflusselektrolyse). Kochsalz schmilzt bei 800 °C

Schmelzenthalpien sind nur selten in Tabellenwerken erfasst.

Die Schmelzenthalpie kann immer dann aus den thermodynamischen Daten abgeleitet werden, wenn Standardbildungsenthalpie-Werte für den festen und flüssigen Aggregatzustand bekannt sind.

1. Schmelzenthalpie Kochsalz: 28; 30,2 kJ/mol (800 °C, Tabellenwerte)
2. Zur praktischen Berechnung der Schmelzwärme werden folgende Tabellenwerte verwendet:
   

NaCl (s) $\longrightarrow$ NaCl (Schmelze)

-411 kJ/mol      -386 kJ/mol                                           Bildungsenthalpien (25 °C)

NaCl (s) $\longrightarrow$ Na⁺ (Schmelze) + Cl^- (Schmelze)

-411 kJ/mol      ca. -215 kJ/mol      ca. -170 kJ/mol           Bildungsenthalpien (25 °C)

$\rightarrow$ Lösungsenthalpie +25 kJ/mol (NaCl, 25 °C)

Bei der Umkehrung dieses Prozesses, der Kristallisation aus der Schmelze, können die Ionen eines Salzes sich direkt zu ihrem festen Kristallgitter zusammenschließen. Während des Ausscheidens von Kochsalzkristallen aus der Schmelze werden -25,2 kJ/mol Kristallisationsenthalpie (bzw. 29±1 kJ/mol bei 800 °C) freigesetzt.

Erfahrungsgemäß können "unterkühlte Salzschmelzen" durch eine spontan einsetzende Kristallisation erhebliche Wärmemengen freisetzen. (Anwendung: Heizkissen).

Gitterenthalpie

Die Gitterenergie beschränkt sich aus Sicht der Chemie auf das thermische Schmelzen der Feststoffstruktur und umfasst allenfalls das Überführen in die Gasphase. Gasförmiges Natriumchlorid besteht aus diskreten NaCl-Molekülen.

Die Gitterenthalpie ist aus Sicht der Physik diejenige Energie, die aufgewendet werden muss, um einen kristallinen ionischen Feststoff in die Gasphase zu überführen (d.i. Sublimationsenergie) und dort im Vakuum in die gasförmigen Ionen zu separieren.

( NaCl ) fest $\longrightarrow$ Na⁺ (g)     +     Cl^- (g)

-411 kJ/mol            611 kJ/mol      -244 kJ/mol           Bildungsenthalpien (25 °C)

$\rightarrow$ Gitterenthalpie +778 kJ/mol

Vergleich: Dies ist ungefähr die doppelte notwendige Energie, die bei der stark exothermen Reaktion von Natriummetall und Chlorgas freiwerden würde. Die Bildung gasförmiger Ionen ist also extrem endotherm.

Die Gitterenthalpie hängt von Größe und Ladung der beteiligten Ionen ab. Die höchste Gitterenthalpie weist Aluminiumoxid Al₂O₃ (Al³⁺ und O^2-) mit 15157 kJ/mol auf. (Siehe auch: Übersicht zur Gitterenthalpie von der Universität Karlsruhe im Abschnitt Web-Links)

Solvatationsenthalpie, Hydratationsenthalpie

Sie gibt an, welche Energie freigesetzt wird, wenn sich gasförmige Ionen an Lösemittel anlagern, also solvatisierte Ionen bilden. Für den häufigsten Fall Solvens = Wasser spricht man von Hydratationsenthalpie.

Na⁺ (g)    $\longrightarrow$    Na⁺ (hydratisiert)

611 kJ/mol            -240 kJ/mol           Bildungsenthalpien (25 °C)

$\rightarrow$ Hydratisierungsenthalpie Na -851 kJ/mol (d.i. extrem exotherm)

Cl^- (g)     $\longrightarrow$     Cl^- (hydratisiert)

-244 kJ/mol            -167 kJ/mol           Bildungsenthalpien (25 °C)

$\rightarrow$ Hydratisierungsenthalpie Cl +77 kJ/mol (d.i. schwach endotherm)

Die Hydratisierungsenthalpie der gasförmigen Ionen von Kochsalz ist mit -774 kJ/mol insgesamt stark exotherm.

Lösungsenthalpie / Kristallisationsenthalpie

Die Lösungsenthalpie von Salzen beinhaltet 1) das Separieren des Ionen-Gitters in Einzel-Ionen und 2) die Solvatisierung der Einzel-Ionen. Teilschritt 1) ist sehr stark endotherm, Teilschritt 2) sehr stark exotherm.

Lösungsenthalpie = Gitterenthalpie + Solvatationsenthalpie.

Lösungsenthalpie NaCl in Wasser = (+778 kJ/mol) + (-851+77 kJ/mol) = +4 kJ/mol (25 °C).

Dieser Wert steht in guter Übereinstimmung mit Tabellenwerken +3,89 kJ/mol für die Kochsalz-Lösungswärme. Beim Lösen tritt also eine ganz geringe Abkühlung der Lösung auf.

Natürlich geht man zur praktischen Berechnungen der Lösungswärme nicht den Umweg über die Gitterenergie, sondern man rechnet direkt und mit nur wenigen Tabellenwerten (gelegentlich findet man den Wert (NaCl)hydrat. = -407 kJ/mol anstelle der Einzel-Ionen):

NaCl (s)   $\longrightarrow$   NaCl (hydratisiert)

-411 kJ/mol          -407 kJ/mol                                        Bildungsenthalpien (25 °C)

NaCl (s)   $\longrightarrow$   Na⁺ (hydratisiert) + Cl^- (hydratisiert)

-411 kJ/mol          -240 kJ/mol            -167 kJ/mol           Bildungsenthalpien (25 °C)

$\rightarrow$ Lösungsenthalpie +4 kJ/mol (Wasser, 25 °C)

Die Solvatationsenthalpie kann immer dann aus den thermodynamischen Daten abgeleitet werden, wenn man Standardbildungsenthalpie-Werte für den festen und gelösten Aggregatzustand findet, z. B. Ameisensäure und Kohlendioxid in obenstehender Tabelle. Sie gilt für "unendliche Verdünnung".

Bei Umkehrung diese Prozesses, der Kristallisation aus Lösung, geben die gelösten Ionen eines Salzes 1) ihre Solvathülle ab und 2) schließen sich in einem festen Kristallgitter zusammen. Während des Ausscheidens von Kochsalzkristallen aus Wasser werden -3,89 kJ/mol Kristallisationsenthalpie freigesetzt.

Intermolekulare Enthalpie-Beiträge

Unterschiedlich starke Wechselwirkungen zwischen den Molekülen sind die Ursache dafür, dass Substanzgruppen ähnliche oder stark unterschiedliche Sublimationsenthalpien aufweisen.

• Schwache Beiträge liefern London-Kräfte, Dipol-Dipol-Wechselwirkungen und Ion-Dipol-Wechselwirkungen mit 1-15 kJ/mol Bindung. Sie werden als van-der-Waals-Wechselwirkung zusammengefasst. Siehe hierzu als Beispiele die Schmelz- und Verdampfungsenthalpien von Wasserstoff, Kohlenmonoxid und Methan.

• Stärkere Beiträge liefern Wasserstoffbrücken-Bindungen mit 20-40 kJ/mol Bindung (je nach Polarisation). Siehe hierzu als Beispiele die Schmelz- und Verdampfungsenthalpien von Wasser, Methanol und Ameisensäure und auch Hydratationsenthalpien. Wasserstoffbrücken-Bindungen sind auch verantwortlich dafür, dass der Siedepunkt von Wasser bei 100 °C liegt, während der von Schwefelwasserstoff nur –83 °C beträgt (siehe Siedepunktanomalie).

• Sehr starke Beiträge liefern Ion-Ion-Wechselwirkungen in Kristallen. Natriumchlorid besteht im Kristall nicht aus diskreten NaCl-Molekülen, sondern aus einer gleichen Anzahl von Natriumkationen und Chloridanionen, die sich im Kristallgitter entsprechend den Coulomb-Kräften exakt angeordnet haben.

Chemische Bedeutung der Enthalpie (Thermochemie)

Die Thermochemie beschreibt im engeren Sinne nur die intramolekularen Kräfte, also die energetischen Beziehungen zwischen den einzelnen Atomen eines Moleküls. Kovalente Bindungen beinhalten ca. 150-1000 kJ/mol Bindungsenergie, ionische Bindungen ca. fünfmal so große Beträge.

Bei Kenntnis der Standardbildungsenthalpien von Edukten und Produkten lässt sich eine mögliche chemische Reaktion energetisch grob bilanzieren. Die wichtigste Frage ist oft, ob ein Prozess endotherm oder exotherm verläuft und wie stark.

$\Delta H_{\mathrm{Reaktion}}^0=\sum \Delta H_{f,\mathrm{Produkte}}^{0} -\sum \Delta H_{f, \mathrm{Edukte}}^{0}$

Durch Details wie Verdampfungs-, Schmelz-, Solvatations- oder Kristallisationsenthalpien können Teilschritte innerhalb der chem. Reaktion energetisch präzisiert werden.

Reaktionsenthalpie

Die Reaktionsenthalpie ist diejenige Energie, die freigesetzt oder benötigt wird, wenn zwischen den Molekülen zweier Stoffe neue chemische Bindungen gebildet werden. Sie ist abhängig von den Reaktionspartnern (Edukte) und der Art der chemischen Bindung im Produkt. Zur Berechnung vergleicht man die Summe der Bindungsenthalpien der Produkte mit der der Edukte. Die Differenz ist die Reaktionsenthalpie.

2 Na (s)      +      Cl₂ (g)    $\longrightarrow$    2 NaCl (s)

2 * 0 kJ/mol        0 kJ/mol               2 * -411 kJ/mol                  Bildungsenthalpien (25 °C)

$\rightarrow$ Reaktionsenthalpie 2*(-411) kJ/mol NaCl (25 °C). Also verläuft die Reaktion exotherm.

Standardverbrennungsenthalpie

Auch die Verbrennung ist eine chemische Reaktion. Die Reaktionsenthalpie der Verbrennungsreaktion bzw. die Standardverbrennungsenthalpie eines Stoffes ist die Enthalpieänderung, die auftritt, wenn ein Stoff unter O₂-Überschuss (O₂-Überdruck) und Standardbedingungen (101,325 kPa und 25 °C) vollständig verbrennt. Definitionsgemäß bezieht sich diese Verbrennungswärme auf die Bildung von gasförmigem Kohlendioxid und flüssigem Wasser (bzw. N₂) als Endprodukte; unter Sauerstoffüberdruck kann sich kein gasförmiges Wasser bilden. Sie wird mit Δ_VH° bezeichnet und ist identisch mit dem Brennwert H_s

In einem Autoklaven-Rohr wird folgende Reaktion mit Sauerstoffüberdruck durchgeführt:

C₃H₈ (g)       +       5 O₂ (g)     $\longrightarrow$     3 CO₂ (g)        +        4 H₂O (l)

-103,2 kJ/mol         5 * 0 kJ/mol             3* -393,5 kJ/mol        4* -286,6 kJ/mol

$\rightarrow$ Reaktionsenthalpie = (3*-393,5 + 4* -285,8) – (1* -103,2 + 5* 0) = -2,22 MJ/mol Propan (25 °C)

Die gleiche Reaktion in einer offenen Brennerflamme; es entstehen nur gasförmige Verbrennungsprodukte::

C₃H₈ (g)       +       5 O₂ (g)     $\longrightarrow$     3 CO₂ (g)        +        4 H₂O (g)

-103,2 kJ/mol         5 * 0 kJ/mol             3* -393,5 kJ/mol        4* -241,6 kJ/mol

$\rightarrow$ Reaktionsenthalpie = (3*-393,5 + 4* -241,8) – (1* -103,2 + 5* 0) = -2,04 MJ/mol Propan (25 °C)

Fortgeschrittene Anwendung

Es ist müßig, sich für jede Reaktion die Standardbildungsenthalpien der Edukte und Produkte zusammen zu suchen, zudem noch im korrekten Aggregatzustand. Zudem stößt man bei größeren Molekülen schnell in ein „Datenvakuum“. Folgende vereinfachte Betrachtungen haben sich in der Praxis bewährt:

1. Es ist unerheblich, ob man ein langkettig alkylsubstituiertes Ethylen bromiert oder Ethylen selbst, die Reaktionswärme pro (C=C)-Doppelbindung ist weitgehend gleich.
2. Es ist unerheblich, ob man eine Reaktion komplett in flüssiger Phase berechnet oder komplett in der Gasphase, die Reaktionswärme beeinflusst dies kaum.
3. Es ist unerheblich (einige Abweichung), wenn man bei 150 °C durchgeführte Reaktionen für 25 °C Standardbedingungen berechnet. (Die Reaktionsenthalpie kann für beliebige Temperaturen berechnet werden bei Kenntnis der Temperaturabhängigkeit der Molwärmen aller Reaktionspartner.)

Daher kann man normale organisch-chemische Umsetzungen wie Halogen-Additionen, Cycloadditionen, Veresterungen mit Säuren oder Anhydriden, Hydrolysen etc. mit Hilfe von zahlreich tabellierten Inkrementen für gasförmige Moleküle nach Benson^[1] berechnen.

Im nachfolgenden Beispiel wird die Reaktionsenergie der Brom-Addition an Ethylen mit Benson-Inkrementen berechnet und zum Vergleich aus Bindungsenergien involvierter Bindungen abgeschätzt. (Merke: Bindungsenergien sind gemittelte Dissoziationsenergien, keine Standardbildungsenthalpien!)

Bromaddition an ein Alken, Reaktionsenthalpie berechnet mit Standardbildungsenthalpien:

H₂C=CH₂       +       Br₂     $\longrightarrow$     H₂BrC-CBrH₂

52 kJ/mol                0 kJ/mol            -39 kJ/mol

$\rightarrow$ Reaktionsenthalpie (25 °C, alle Werte für gasförm. Zustand) = (-39 - 52) = -91 kJ/mol Doppelbindung

Bromaddition an ein Alken, Reaktionsenthalpie berechnet mit Inkrementen nach Benson:

H₂C=CH₂       +       Br₂     $\longrightarrow$     H₂BrC-CBrH₂

2 C_d-(H)₂ = 2* +28,1 kJ/mol               2 C-(H)₂(Br)(C) = 2* -22,6 kJ/mol

$\rightarrow$ Reaktionsenthalpie (berechnet nach Benson) = ( -45,2 - (+56,2)) = -101 kJ/mol Doppelbindung

Bromaddition an ein Alken, Reaktionsenthalpie abgeschätzt mit Bindungsenergien:

H₂C=CH₂       +       Br₂     $\longrightarrow$     H₂BrC-CBrH₂

4 C-H : 4*>455 kJ/mol                       4 C-H : 4* 380±50 kJ/mol

1 C=C : 1* 614 kJ/mol                       1 C-C : 1* 348 kJ/mol

1 Br-Br : 193 kJ/mol                          2 C-Br : 2* 260±30 kJ/mol

$\rightarrow$ Reaktionsenthalpie (geschätzt aus Bindungsenergien) = ( 2388±200 - 2627) = -239±200 kJ/mol Doppelbindung

Die beste Abschätzung für Reaktionsenthalpien gelingt mit Standardbildungsenthalpien oder Inkrementen nach Benson, bei Verwendung von „Bindungsenergien“ ist die Unsicherheit mit ±200 kJ/mol viel zu hoch.

Technische Anwendbarkeit

Die Reaktionsenthalpien GLARS organischer Reaktionen liegen im Bereich -160 bis +100 kJ pro mol "reaktiver Zentren". Als sehr stark exotherm erweisen sich alle Additionsreaktionen mit Epoxiden, Anhydriden und Halogenen. Diese thermochemischen Betrachtungen treffen keine Aussage darüber, wie schnell diese Reaktionswärmen freigesetzt werden. Sie machen nur die Aussage, bis zum Reaktionsende wird diese Wärme freigesetzt. Jede Reaktion erhöht ihre Geschwindigkeit um das Zwei- bis Dreifache bei Temperaturerhöhung um 10 K. Umgekehrt bedeutet eine zweifache Verdünnung der Reaktionspartner häufig eine Halbierung der Reaktionsgeschwindigkeit bzw. Wärmeleistung der Reaktion. Berechnete Reaktionsenthalpien dienen dazu, in einem System von Reaktanten und Lösemittel über deren Wärmekapazitäten den Temperaturverlauf zu berechnen. Großtechnische Anlagen verfügen nur über begrenzte Kühlkapazitäten (-Wärme/Zeit), dies bleibt im Laborversuch häufig wenig berücksichtigt.

Bindungsenergie / Dissoziationsenergie

Die Bindungsenergie bzw. Bindungsstärke gibt die "Stabilität" der Atombindung an. Die Bestimmung ist nur bei zweiatomig symmetrischen Molekülen wie z. B. Wasserstoff oder Halogene direkt möglich. In diesen Fällen kann die Dissoziationsenergie zur Bildung zweier identischer Radikale einfach gemessen/berechnet werden. Bei "Element-Radikalen" bezeichnet man die Standardbildungsenthalpie von Radikalen auch als Atomisierungsenthalpien.

In allen anderen Fällen sind Werte für die "Bindungsenergie" nur indirekt möglich durch Vergleich mehrerer Dissoziationsenergie-Messungen an homologen Molekülen. Die Werte schwanken abhängig vom Substitutionsmuster an den Radikal-Zentren.

Die Standardbildungsenthalpie von gasförmigen BROM-Radikalen beinhaltet die Verdampfungsenthalpie (31 kJ/mol), die notwendig ist, um flüssiges Brom in die Gasphase zu transportieren. Die Standardbildungsenthalpie von gasförmigen IOD-Radikalen beinhaltet die Sublimationsenthalpie (62 kJ/mol), die notwendig ist, um kristallines Iod in die Gasphase zu transportieren. Die Standardbildungsenthalpie von gasförmigen KOHLENSTOFF-Radikalen ist identisch mit der Standardbildungsenthalpie von gasförmigem Kohlenstoffdampf.

Joule-Thomson-Effekt (Erzeugung tiefer Temperaturen)

Physikalisch ist die auf die Stoffmenge bezogene molare Enthalpie H_m: = H / mol u.a. deshalb von besonderer technischer Bedeutung, weil sie im Gegensatz zu anderen Größen beim Joule-Thomson-Prozess, dem stationären Durchströmen eines fluiden Systems durch ein Rohr mit einem sog. „Drosselventil“ (d.h. einer sehr starken Verengung zwecks Druckabnahme) konstant ist, obwohl sich auf beiden Seiten des Ventils unterschiedliche Drücke ausgebildet haben.

Diese Besonderheit, und der damit verbundene sog. Joule-Thomson-Effekt, wird großtechnisch zur Verflüssigung verschiedener Gase nach dem Linde-Verfahren ausgenutzt.

Siehe auch

• Thermodynamisches Potential
• Gibbs-Energie
• Isobar
• Isenthalp
• Dortmunder Datenbank
• Wärmeinhalt
• Gruppenbeitragsmethoden (zur Vorhersage von Verdampfungsenthalpien)

Literatur

1. ↑ Benson S.W., Cruickshank F.R., Golden D.M., Haugen G.R., O'Neal H.E., Rodgers A.S., Shaw R., Walsh R., Additivity Rules for the Estimation of Thermochemical Properties, Chem. Rev., 69, 279-324, 1969

Weblinks

• Übersicht zur Gitterenthalpie von der Universität Karlsruhe (PDF-Format)