- Verhältnis (Mathematik)
-
In der Mathematik und in den Naturwissenschaften bezeichnet der Quotient ein Verhältnis von zwei Größen zueinander, also das Ergebnis einer Division. Der Quotient von zwei ganzen Zahlen (Dividend und Divisor) ist immer eine rationale Zahl und kann als Bruch geschrieben werden.
Ein Quotient dient oftmals der Einordnung eines Wertes in einen Gesamtmaßstab, so z. B. der Intelligenzquotient, der die mit einem Intelligenztest ermittelte Zahl für eine Person mit der ihrer Altersgruppe entsprechenden "durchschnittlichen Intelligenz" in Beziehung setzt. Der Intelligenzquotient 100 steht dabei für den Durchschnitt. Verhältnisse werden häufig in Prozent angegeben, indem das Verhältnis so normiert (also erweitert oder gekürzt) wird, dass der Nenner 100 ist.
Besondere Verhältnisse in diesem Sinne sind:
- Die Steigung als Verhältnis des Wertzuwachses auf der zweiten Koordinatenachse zum Wertzuwachs auf der ersten Koordinatenachse.
- Die trigonometrischen Funktionen Sinus, Cosinus usw.
- Der Maßstab als Verhältnis zweier Längen
- Der Radius als das Doppelte des Verhältnisses zwischen Kreisfläche und Kreisumfang
- Die Fraktale Dimension der Chaostheorie als Verhältnis zweier Logarithmen
Inhaltsverzeichnis
Proportionen
Als Verhältnisgleichungen oder Proportionen werden Gleichungen bezeichnet, die zwei Verhältnisse gleichsetzen. Sie haben also die Form a÷b = c÷d. a und c heißen auch Vorderglieder, b und d Hinterglieder der Proportion. Darüber hinaus heißen a und d Außenglieder sowie b und c Innenglieder. Die Proportion kann durch Kreuzmultiplikation in eine Gleichung der Form a·d = c·b umgeformt werden. Durch Vertauschen der Innenglieder bzw. der Außenglieder einer Proportion entstehen neue Proportionen: a÷c = b÷d und d÷b = c÷a. Darüber hinaus gelten die Gesetze der korrespondierenden Addition und Subtraktion:
Gesetze der korrespondierenden Addition und Subtraktion
Es sei die Proportion a÷b = c÷d gegeben. Dann gelten auch die Proportionen
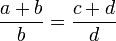 und
und 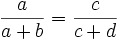 und
und 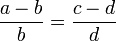 und
und 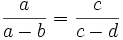 und
und 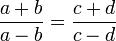
Fortlaufende Proportionen
Gelegentlich findet sich auch die Schreibweise a÷b÷c = u÷v÷w. Diese fortlaufenden Proportionen sind nicht als eine einzelne Gleichung zu verstehen, sondern sind vielmehr ein Kurzform für die beiden Gleichungen a÷b = u÷v und b÷c = v÷w (bzw. äquivalent a÷u = b÷v und b÷v = c÷w).[1]
Beispiele
- Die Definition des Goldenen Schnitts
- Der Sinussatz
- Die Strahlensätze
- Das Brechungsgesetz der Optik
- Die Oktave der Musik
Einzelnachweise
- ↑ Walter Gellert, Herbert Kästner, Siegfried Neuber (Hrsg): Lexikon der Mathematik, VEB Bibliographisches Institut Leipzig, 1979. S 447, Proportion.
Weblinks
Wikimedia Foundation.
