Streckung (Mathematik)

Zentrische Streckung mit positivem Streckungsfaktor

Zentrische Streckung mit negativem Streckungsfaktor

Unter einer zentrischen Streckung versteht man in der Geometrie eine Abbildung, die alle Strecken in einem bestimmten, gegebenen Verhältnis vergrößert oder verkleinert, wobei die Bildstrecken jeweils zu den ursprünglichen Strecken parallel sind. Zentrische Streckungen sind spezielle Ähnlichkeitsabbildungen.

Definition

Gegeben seien ein Punkt Z der Zeichenebene oder des Raumes und eine reelle Zahl 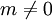$m \ne 0$. Die zentrische Streckung mit Zentrum Z und Streckungsfaktor (Abbildungsfaktor) m ist diejenige Abbildung der Zeichenebene beziehungsweise des Raumes in sich, bei der der Bildpunkt P' eines Punktes P folgende Eigenschaften besitzt:

• Z, P und P' liegen auf einer Geraden.
• Für m > 0 liegen P und P' auf derselben Seite von Z, für m < 0 auf verschiedenen Seiten.
• Die Streckenlänge 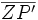$\overline{ZP'}$ ist gleich dem | m | -fachen der Streckenlänge $\overline{ZP}$.

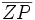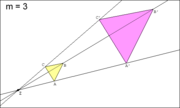
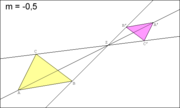
Die beiden Skizzen zeigen die Anwendung zweier zentrischer Streckungen (mit m = 3 und m = − 0,5) auf jeweils ein Dreieck ABC.

Eigenschaften

• Zentrische Streckungen sind geraden- und winkeltreu.
• Die Längenverhältnisse bleiben erhalten.
• Die Bildstrecke einer beliebigen Strecke hat die | m | -fache Länge.
• Eine beliebige geometrische Figur wird auf eine Figur mit dem m²-fachen Flächeninhalt abgebildet.
• Ein beliebiger Körper wird auf einen Körper mit dem | m | ³-fachen Volumen abgebildet.
• Die zentrischen Streckungen mit einem bestimmten Zentrum bilden algebraisch gesehen eine Gruppe.
• Das Bild einer Geraden ist eine Parallele zu der Geraden.
• In vektorieller Schreibweise wird die zentrische Streckung mit Zentrum Z und Streckungsfaktor m beschrieben durch

P' = Z + m(P − Z) = mP + (1 − m)Z.

• Damit ist eine zentrische Streckung die Affinität (Mathematik), die durch die Matrix mE_n und den Verschiebungsvektor (1 − m)Z beschrieben wird.

Spezialfälle

Für m = 1 ergibt sich die identische Abbildung (Identität), für m = − 1 eine Punktspiegelung. Der Fall m = 0 ist nicht erlaubt, da sonst alle Punkte denselben Bildpunkt hätten, nämlich das Zentrum.

Verallgemeinerung

Die zentrische Streckung ist ein Beispiel für eine Dilatation. In der axiomatisch aufgebauten affinen Geometrie wird dieser Begriff mithilfe der Parallelität definiert.

Siehe auch

• Strahlensatz

Literatur

• H. Schupp: Elementargeometrie, UTB Schoeningh (1977)