Verhältniszahl

Eine dimensionslose Größe (korrekte Bezeichnung: Größe der Dimension Eins) ist eine physikalische Größe, die durch eine reine Zahl ohne Maßeinheit angegeben werden kann. Zwar werden der Deutlichkeit zuliebe in manchen Fällen auch hier Einheiten verwendet, jedoch entspricht einer solchen Einheit (Hilfsmaßeinheit) keine Dimension.

Es gibt mehrere Gruppen dimensionsloser Größen, so beispielsweise

• Verhältnisgrößen, das sind physikalische Größen, die durch eine Division zweier Größen gleicher Größenart beschrieben werden.
• dimensionslose relative Kennzahlen, das sind beschreibende Parameter eines Systems, meist im Sinne einer Materialkonstante oder einer systemtypischen Allgemeinbeschreibung
• spezielle Größen der Physik, die durch reine Zahlen beschrieben werden

Beispiele

Beispiele für dimensionslose Größen sind

• Anzahlen, auch, wenn sie in einem Zählmaß wie beispielsweise Dutzend angegeben sind
• Angaben in Verhältniseinheiten wie beispielsweise Prozent, Promille, ppm
• Ebene Winkel und Raumwinkel (Basiseinheiten Radiant bzw. Steradiant)
• Verhältniszahlen, d.h. Quotienten aus zwei dimensionsgleichen Größen
• logarithmierte Verhältniszahlen wie Bel, Neper, Phon
• dimensionslose Kennzahlen
• Wahrscheinlichkeiten
• Quantenzahlen

Verhältniszahlen sind bezogene Größen, deren Bezug jeweils von derselben Größenart ist (z. B. Wirkungsgrad).

Wichtig sind die dimensionslosen Kennzahlen der Fluiddynamik und Thermohydraulik als intensive Größen, anhand derer man das Systemverhalten vorhersagen kann bzw. die einen Vergleich zwischen verschiedenen Systemen (unterschiedlicher Abmessung) ermöglichen. Hierzu zählt zum Beispiel die Reynolds-Zahl, die die Strömungsqualität (laminar/turbulent) charakterisiert.

Ein Beispiel aus einem anderen Gebiet ist die Sommerfeldsche Feinstrukturkonstante, die sich aus elektrischer Elementarladung, Planckschem Wirkungsquantum und der Lichtgeschwindigkeit zusammensetzt. Ihr Wert beträgt etwa 1/137. Diese Konstante wurde von Arnold Sommerfeld 1916 eingeführt, um die durch Magnetfelder bedingte Feinstrukturaufspaltung von Spektrallinien berechnen zu können.

Größenbenennungen nach DIN 5485

Nach DIN 5485 Benennungsgrundsätze für physikalische Größen; Wortzusammensetzungen mit Eigenschafts- und Grundwörtern ist für dimensionslose Größen vorgesehen:

• -zahl
• -beiwert
• -faktor
• -grad
• -quote
• -verhältnis
• -anteil

Tatsächlich halten sich im wissenschaftlichen und technischen Alltag aber zahlreiche Bezeichnungen, die diesen Kriterien nicht folgen, und dimensionslose physikalische Größen lassen sich oft, aber nicht immer, an der Endung -zahl erkennen. Auch die Endung -koeffizient bezeichnet manchmal, aber nicht immer eine dimensionslose Größe. Im anderen Falle handelt es sich um bezogene Größen (die meist auf eine Masse, ein Gewicht, Volumen oder ähnliches normiert sind). Beispiele:

• Brechzahl
• Permeabilitätszahl
• Reibungskoeffizient (dimensionslos)
• Wärmeausdehnungskoeffizient (nicht dimensionslos)

Theoretischer Hintergrund

In der Metrologie hat eine Größe die Dimension 1, wenn sie keiner Dimension des jeweils gewählten Größensystems zugeordnet ist. Dies zeigt sich z. B. daran, dass bei der Darstellung der entsprechenden Dimension als Potenzprodukt aus den Basisdimensionen jede Potenz null ist. Dass eine Größe keiner Dimension angehört, kann prinzipiell zwei Gründe haben:

1. sie ist der Quotient zweier Größen derselben Dimension
2. sie wurde noch nicht per Definition einer Dimension zugeordnet

Beispiel: In einem Größensystem mit nur den zwei Basisdimensionen Länge L und Masse M hat die Länge die Dimension $L^1 \cdot M^0 = L$.

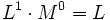1. Eine Größe, die als Quotient aus zwei Größen der Dimension L definiert ist, hat dann immer die Dimension L / L = 1.
2. Eine Zeitspanne hätte dann zunächst die Dimension 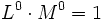$L^0 \cdot M^0 = 1$. Durch eine zusätzliche Definition könnte sie jedoch dimensionsbehaftet gemacht werden, z. B. durch Zuordnung zur Dimension L³ oder zu einer neu eingeführten Basisdimension Zeit T

Da man im Prinzip (siehe Relativitätstheorie) Zeit und Länge als ein und dieselbe Größenart ansehen kann (anstatt als getrennte Basisgrößen wie z. B. im SI-System), könnte man auch die Geschwindigkeit als dimensionslose Verhältnisgröße betrachten. Jedoch geschieht das in den praktisch verwendeten Einheitensystemen nicht: aus historischen Gründen, wegen der Anschaulichkeit und wegen der "Unhandlichkeit" des Umrechnungsfaktors Vakuum-Lichtgeschwindigkeit (1 s würde als Längeneinheit ca. 300.000 km entsprechen). In der theoretischen Physik wird aber oft die Vakuum-Lichtgeschwindigkeit gleich 1 gesetzt (siehe Natürliche Einheiten).

Grundsätzlich hängt es von der für ein Größensystem gewählten Basis ab, welche abgeleiteten Größen welche Dimension haben, und somit auch, welche Größen (außer den Quotienten dimensionsgleicher Größen) die Dimension 1 haben. So sind in elektrostatischen cgs-Systemen elektrische Kapazität und Länge von gleicher Dimension; jeder Quotient dieser Größen erhält daher die Dimension 1.

Hinter der Wahl der Basis eines Größensystems steckt letztlich die Frage, wie man über die Proportionalitätskonstanten in der Schreibweise physikalischer Gesetze verfügt.

Ausschließlich die kohärenten dimensionslosen Maßeinheiten eines Einheitensystems – von denen es zu jeder Größenart nur eine gibt – nehmen dimensionslose Einheiten beim Rechnen mit den anderen Einheiten des Systems auch den Zahlenwert 1 an. So kann innerhalb des SI-Einheitensystems 1 Radiant = 1 geschrieben werden, nicht aber, wenn mit der nicht kohärenten dimensionslosen Maßeinheit Grad gerechnet wird.

Siehe auch

• Dimensionsanalyse

Literatur

• The International System of Units. SI brochure (8th ed.). Bureau International des Poids et Mesures. Mai 2006. (weblink PDF/Onlineversion) – insbesondere Kapitel 2.2.3 Units for dimensionless quantities, also called quantities of dimension one