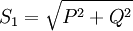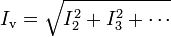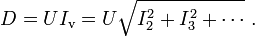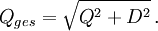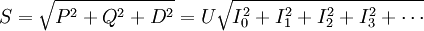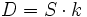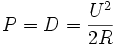Verzerrungsleistung

Die Verzerrungsblindleistung ist ein Begriff aus der Elektrotechnik und beschreibt eine spezielle Form der Blindleistung, die in Wechsel- bzw. Drehstromnetzen durch nichtlineare Verbraucher verursacht wird. Die Bezeichnung wird in der Literatur nicht einheitlich gewählt. Alternative Bezeichnungen sind Verzerrungsleistung, Oberschwingungsblindleistung oder Oberwellenblindleistung.

Allgemeines

Stromversorgungsnetze werden praktisch ausschließlich mit sinusförmiger Wechselspannung betrieben. Daher hat bei linearen elektrischen Bauelementen wie elektrischen Widerständen oder sogenannten Blindwiderständen der Strom auch einen sinusförmigem Verlauf. Es tritt dann keine Verzerrungsblindleistung auf.

Die Ursache der Verzerrungsblindleistung sind nichtlineare elektrische Baugruppen, wie Gleichrichter in Netzteilen, Wechselrichter oder auch magnetische Bauteile, die magnetische Sättigungserscheinungen zeigen. Diese Baugruppen verursachen in den Leitungen nichtsinusförmige Wechselströme. Dieser nichtsinusförmige Verlauf ist als eine Summe von sogenannten Oberschwingungen darstellbar. Diese Oberschwingungen des Stromes in Kombination mit der sinusförmigen Netzspannung ergeben Blindleistungsanteile, die als Verzerrungsblindleistung bezeichnet werden.

Der Begriff rührt daher, dass nichtlineare elektrische Bauteile den sinusförmigen zeitlichen Verlauf des Stromes verzerren. Die dabei auftretenden Oberschwingungen können auch die Ursache von Störungen sein.

Berechnung

Zeigerdiagramm der Wirkleistung P, Blindleistung Q und Verzerrungsblindleistung D

Die Wirkleistung P ist jene Leistung, die an einem Verbraucher tatsächlich entsprechende Leistung erbringt, beispielsweise Drehbewegung eines Elektromotors oder die Temperatursteigerung einer Elektroheizung. Die Grundschwingungs-Blindleistung 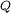$\scriptstyle{Q\,}$ ist eine Leistungskomponente, die infolge der Energiespeicherung in den induktiven oder kapazitiven Anteilen der Verbraucher periodisch zwischen Erzeuger (Kraftwerk) und Verbraucher hin- und herpendelt und an sich unerwünscht ist, da sie Leitungen zusätzlich belastet. Die Grundschwingungs-Scheinleistung 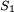$\scriptstyle{S_1\,}$ ist die vektorielle Summe aus Wirkleistung und Grundschwingungsblindleistung:

$S_1 = \sqrt{P^2 + Q^2}$

Bei Oberschwingungen kommt eine dritte Komponente, die Verzerrungsblindleistung D hinzu, welche die Blindleistung in den Oberschwingungen darstellt. Ist 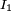$\scriptstyle{I_1\,}$ der Effektivwert des Grundschwingungsstromes, 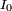$\scriptstyle{I_0\,}$ der Gleichstromanteil des Stromes und 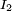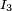$\scriptstyle{I_2\,}$, $\scriptstyle{I_3\,}$ usw. die Effektivwerte der Oberschwingungsströme, U der Effektivwert der Spannung, so lässt sich der Verzerrungsblindstrom als

$I_{\mathrm v} = \sqrt{I_2^2 + I_3^2 + \cdots}$

ausdrücken und die Verzerrungsblindleistung als

$D = U I_{\mathrm v} = U \sqrt{I_2^2 + I_3^2 + \cdots} \,\,.$

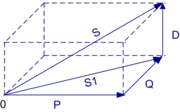
Die gesamte Blindleistung, in nebenstehender Abbildung nicht explizit dargestellt, ergibt sich aus der Grundschwingungsblindleistung und der Verzerrungsblindleistung zu

$Q_{ges} = \sqrt{Q^2 + D^2}\,.$

Der gesamte Betrag der Scheinleistung S ist im allgemeinen Fall gegeben durch:^[1]

$S = \sqrt {P^2 + Q^2 + D^2} = U \sqrt{I_0^2 + I_1^2 + I_2^2 + I_3^2 + \cdots}$

In nebenstehender Abbildung ist das Zeigerdiagramm mit den Zeigern für die verschiedenen Leistungen dargestellt.

Zusammenhang mit dem Klirrfaktor

Die Verzerrungsblindleistung lässt sich auch mit dem Klirrfaktor k und der Scheinleistung S ausdrücken:

$D = S \cdot k$

Beispiele

• Bei idealen, linearen Blindwiderständen wie Kondensatoren oder Induktivitäten tritt keine Verzerrungsblindleistung D auf, sondern ausschließlich die Grundschwingungsblindleistung $\scriptstyle{Q\,}$.
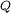• Bei einem mit einer Diode in Serie geschalteten ohmschen Lastwiderstand R, z. B. einer Glühlampe, tritt an einer sinusförmigen Wechselspannungsquelle mit der Effektivspannung U zwar keine Blindleistung 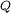$\scriptstyle{Q\,}$ in der Grundschwingung auf, da der Energiespeicher fehlt, sondern nur eine Wirkleistung P und Verzerrungsblindleistung D infolge der Oberschwingungen. Bemerkenswert dabei ist, dass in dieser Schaltung, in der die Glühlampe R mit dem Einweggleichrichter betrieben wird, die Wirkleistung P betragsmäßig gleich groß wie die Verzerrungsblindleistung D ist und den Betrag

$P = D = \frac{U^2}{2R}$

aufweist. Da diese Einweggleichrichtung dem Laststrom einen Gleichstromanteil aufprägt, ist bei größeren Leistungen diese Form des einfachen Dimmens von Glühlampen durch Vorschalten einer Diode nicht mehr zulässig. Der vorgeschaltete Ortsnetztransformator könnte ansonsten vormagnetisiert werden und damit im ungünstigsten Fall in die Sättigung geraten.

Siehe auch

• Blindstrom
• Leistungsfaktor
• Leistungsfaktorkorrekturfilter

Literatur

• Flosdorff, Hilgarth: Elektrische Energieverteilung, Teubner Verlag, 2003, ISBN 3-519-26424-2

Einzelnachweise

1. ↑ Ruhr-Universität Bochum, Lehrstuhl für elektrische Energietechnik und Leistungselektronik: Grundlagen der Energietechnik., 25.08.2004, S. 55.