Vierergruppe von Klein

In der Algebra ist die Kleinsche Vierergruppe die kleinste nicht-zyklische Gruppe. Sie ist benannt nach Felix Klein (der sie in seinen „Vorlesungen über das Ikosaeder“ 1884 Vierergruppe nannte) und wird oft mit dem Buchstaben V bezeichnet.

Ihre Verknüpfungstabelle ist diese:

*	1	a	b	c
1	1	a	b	c
a	a	1	c	b
b	b	c	1	a
c	c	b	a	1

Die Vierergruppe tritt z. B. auf als Symmetriegruppe eines Rechtecks (sofern es kein Quadrat ist, $a\ne b$):

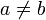Die vier Elemente sind dabei: die Identität, die Spiegelung an der waagerechten Mittelachse, die Spiegelung an der senkrechten Mittelachse, und die 180 Grad-Drehung um den Mittelpunkt.

Die drei Elemente ungleich der Identität haben die Ordnung 2. Die Vierergruppe ist abelsch und isomorph zu Z/2Z × Z/2Z und zur Diedergruppe der Ordnung 4 (D₂).

Eine Permutationsdarstellung von V liefert die Nummerierung der Ecken des obigen Rechtecks:

V = {id, (1,2)(3,4), (1,3)(2,4), (1,4)(2,3)}.

In dieser Darstellung ist V die Kommutatorgruppe und damit ein Normalteiler der alternierenden Gruppe A₄ und auch Normalteiler der symmetrischen Gruppe S₄. In der Galoistheorie erklärt die Existenz der Kleinschen Vierergruppe in dieser Darstellung die Existenz der Lösungsformel für Gleichungen vierten Grades.

Man kann die Vierergruppe auch darstellen als Automorphismengruppe des folgenden Graphen:

   *----*
   *----*----*

Die Einheitengruppe des Ringes Z/8Z, das sind die Restklassen von 1, 3, 5 und 7 unter Multiplikation modulo 8, ist isomorph zu V.