KV-Algorithmus

Bild 1-1: Karnaugh-Veitch-Diagramm: ¬AB¬C¬D ∨ A¬B¬C¬D ∨ A¬B¬CD ∨ A¬BC¬D ∨ A¬BCD ∨ AB¬C¬D ∨ ABC¬D ∨ ABCD = AC ∨ B¬C¬D ∨ A¬B

Bild 1-2: Karnaugh-Veitch-Diagramm: ABCD ∨ AB¬CD ∨ ¬AB¬CD ∨ A¬BC¬D ∨ ¬A¬BC¬D ∨ ¬A¬B¬CD = ABD ∨ ¬A¬CD ∨ ¬BC¬D

Das Karnaugh-Veitch-Diagramm (bzw. das Karnaugh-Veitch-Symmetrie-Diagramm, die Karnaugh-Tafel oder der Karnaugh-Plan), kurz KV-Diagramm, KVS-Diagramm oder K-Diagramm (engl. Karnaugh map), dient der übersichtlichen Darstellung und Vereinfachung Boolescher Funktionen – Umwandlung der disjunktiven Normalform in einen minimalen logischen Ausdruck. Es wurde 1952 von Edward W. Veitch [viːtʃ] entworfen und 1953 von Maurice Karnaugh [ˈkɑːɹnɔː] zu seiner heutigen Form weiterentwickelt.

Eigenschaften

Mittels eines KV-Diagramms lässt sich jede beliebige disjunktive Normalform (DNF) in einen minimalen logischen Ausdruck umwandeln. Der Vorteil gegenüber anderen Verfahren ist, dass der erzeugte Term (meist) minimal ist. Sollte der Term noch nicht minimal sein, ist eine weitere Vereinfachung durch Anwenden des Distributivgesetzes (Ausklammern) möglich. Das Umwandeln beginnt mit dem Erstellen einer Wahrheitstafel, aus der dann die DNF abgeleitet wird, die dann wiederum direkt in ein KV-Diagramm umgewandelt wird.

Da sich benachbarte Felder jeweils in einer Variable nur um ein Bit unterscheiden, ist folgende Regel anwendbar: A ∨ ¬A = 1. Auf dieser Regel basiert die Reduzierung der Gruppen.

Die inverse Funktion 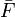$\bar{F}$ findet man durch Vertauschen von „1“ und „0“ im KV-Diagramm.

Ein KV-Diagramm ist ebenfalls nützlich, um Hazards festzustellen und zu eliminieren.

Das Ausfüllen des KV-Diagramms

Ein KV-Diagramm für n Eingangsvariablen hat 2ⁿ Felder (siehe Beispiel). Das KV-Diagramm wird mit den Variablen an den Rändern beschriftet. Dabei kommt jede Variable in negierter und nicht-negierter Form vor. Die Zuordnung der Variablen zu den einzelnen Feldern kann dabei beliebig erfolgen, jedoch ist zu beachten, dass sich horizontal und vertikal benachbarte Felder nur in genau einer Variablen unterscheiden dürfen. Mit Hilfe der Wahrheitstabelle der zu optimierenden Funktion wird in die einzelnen Felder eine 1 eingetragen, wenn ein Minterm der Funktion vorliegt, andernfalls eine 0. Ein Minterm m der Funktion liegt dann vor, wenn gilt

$m(\underline X) = 1 \Rightarrow F(\underline X) = 1$,

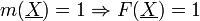wobei 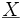$\underline X$ der Vektor der Eingangsvariablen ist. In einer disjunktiven Normalform gilt dies für jeden Konjunktionsterm, der 1 liefert, da dann auch die Gesamtdisjunktion und folglich auch die Funktion 1 liefert. KV-Diagramme eignen sich für die Vereinfachung von Funktionen mit bis zu 5 Eingangsvariablen.

Vereinfachung

Sind weniger Felder des KV-Diagramms mit 0 als mit 1 ausgefüllt, wählt man die Minterm-Methode, andernfalls die Maxterm-Methode.

Minterm-Methode

Bild 2-1: Nachbarfelder des „Einser“-Feldes – rote Felder

Bild 2-2: Nachbarfelder des „Einser“-Feldes – rote Felder

Bild 2-3: Nachbarfelder des „Einser“-Feldes – rote Felder

• Man versucht, möglichst viele horizontal und vertikal benachbarte Felder, die eine 1 enthalten (Minterme) zu zusammenhängenden 2er-, 4er-, 8er- oder 16er-Blöcken (sogenannten Päckchen) zusammenzufassen. Als Blockgröße sind alle Potenzen von 2 erlaubt, bei denen der Exponent eine natürliche Zahl größer Null und höchstens so groß wie die Anzahl der Variablen ist. Bei Zwei bis Fünf Variablen ergeben sich damit folgende Werte:
  • Zwei Variablen: 2 oder 4 Felder pro Päckchen.
  • Drei Variablen: 2, 4 oder 8.
  • Vier Variablen: 2, 4, 8 oder 16.
  • Fünf Variablen: 2, 4, 8, 16 oder 32.

Je nach Wertetabelle kann es jedoch vorkommen, dass es in der KV-Tafel eine alleinstehende 1 gibt. Diese alleinstehende 1 muss natürlich bei dem späteren Bilden der Schaltgleichung auch mit berücksichtigt werden.

• Ein Block kann unter Umständen über den rechten bzw. unteren Rand des Diagramms fortgesetzt werden. Dies erklärt sich folgendermaßen: KV-Diagramme für drei Variablen müssen im Grunde als Zylinder verstanden werden. Die Felder ganz links und ganz rechts sind also benachbart. KV-Diagramme für vier Variablen müssen im Grunde als Torus („Donut-Form“) verstanden werden. Die vier Ecken des quadratisch gezeichneten KV-Diagrammes sind im Grunde benachbart. Noch komplexere Nachbarschaftsbeziehungen gelten für 5 oder mehr Variablen. Da multidimensionale Gebilde zeichnerisch schwierig zu handhaben sind, wählt man die Darstellung in der Ebene, muss dann aber die Nachbarschaftsbeziehungen im Sinn behalten.
• Die gebildeten Päckchen wandelt man nun in Konjunktionsterme um. Dabei werden Variablen innerhalb eines Blockes, die in negierter und nicht negierter Form auftreten, weggelassen.
• Diese UND-Verknüpfungen werden durch ODER-Verknüpfungen zusammengefasst und ergeben eine disjunktive Normalform.

Maxterm-Methode

Die Maxterm-Methode unterscheidet sich von der Minterm-Methode lediglich in folgenden Punkten:

• Statt Einsen werden Nullen zu Päckchen zusammengefasst.
• Ein Päckchen bildet einen Disjunktionsterm (ODER-Verknüpfungen, statt eines Konjunktionsterms).
• Die Disjunktionsterme werden konjunktiv (mit UND) verknüpft.
• Die Variablen werden zusätzlich einzeln negiert.

Ringsummen-Methode

Es gibt auch eine Möglichkeit eine sogenannte Ringsummen-Normalform aus einem KV-Diagramm abzulesen. Dazu wählt man die Blöcke aus Nullen und Einsen so, dass die Nullen von einer geraden und die Einsen durch eine ungerade Anzahl von Blöcken überdeckt werden. Die Terme werden dann mit XOR verknüpft und ergeben eine minimierte Funktion.

Veranschaulichung durch Hyper-Einheitswürfel

Bild 3-1: Hyperwürfel

Boolesche Funktionen mit n Variablen lassen sich grafisch mittels Einheitswürfeln der Dimension n veranschaulichen. Würfel beliebiger Dimension bezeichnet man auch als Hyperwürfel. Da Karnaugh-Diagramme selbst eine spezielle Darstellungsform für Boolesche Funktionen sind, überrascht es nicht, dass sich zwischen Hyper-Einheitswürfeln und Karnaugh-Diagrammen ein anschaulicher Zusammenhang herstellen lässt. Und zwar entsprechen Karnaugh-Diagramme für n Variablen umkehrbar eindeutig den Hyper-Einheitswürfeln der Dimension n. Die Ecken-Koordinaten des Hyperwürfels entsprechen dabei den dualen Nummern der Felder im Karnaugh-Diagramm.

Bild 3-2 zeigt den Einheitswürfel für 3 Variablen. Das entspricht einem 2x4 KV-Diagramm. Das KV-Diagramm in Bild 3-3 ist in Bild 3-4 entsprechend markiert (grüne Ebene). Die Knoten (Eckpunkt oder Kreise) am Hyper-Einheitswürfel entsprechen jeweils einem Feld im KV-Diagramm. Die Übergänge (Nachbarschaft der Felder) sind durch die Kanten des Würfels symbolisiert. Beim Wandern auf der Kante entsteht ein Gray-Code. Auf jeder Kante ändert sich genau 1 Bit. Eine wesentliche Eigenschaft ist, dass sich die Gray-Codes für zwei benachbarte Zahlen nur um 1 Ziffer, bei Binärcode also 1 Bit, unterscheiden (Hamming-Distanz).

Das KV-Diagramm hat so viel Nachbarschaften, wie der Würfel Kanten hat. Bild 3-5 zeigt eine ebene Darstellung des Hyper-Einheitswürfels. Ohne seine innere Struktur der Übergänge zu ändern lässt sich der Würfel in beliebige Richtungen „umstülpen“, wie in der Animation in Bild 3-9 dargestellt ist. So ist zu erklären, warum es KV-Diagramm mit verschiedenen Anordnungen der Variablen gibt (Randbeschriftung). Sie wurden praktisch wie ein Würfel „umgestülpt“.

Bild 3-2

Bild 3-3

Bild 3-4

Bild 3-5

Für das KV-Diagramm mit 2 Variablen (2x2 Feld) ergibt sich ein einfacherer Hyper-Einheitswürfel (Bild 3-6). Bei 1 Variable ist der „Würfel“ trivial (Bild 3-7). Mit zunehmenden Variablen steigt die Anzahl der Kanten allerdings exponentiell an. So gibt es bei 4 Variablen (Bild 3-8) bereits 32 Kanten.

Bild 3-6

Bild 3-7

Bild 3-8

Bild 3-9

Don’t-Care-Zustände

Bild 4: Beispiel für Don’t-Care-Zustände

Häufig gibt es Boolesche Funktionen mit Wahrheitstabellen, in denen nicht für jede Kombination der Eingangsvariablen ein Wert der Ausgangsvariablen definiert sein muss. Man nennt solche Ausgangszustände Don’t-Care-Terme und bezeichnet sie mit X, da sie sowohl den Wert 1 als auch 0 annehmen können. Diese X-Felder dürfen als 1 oder 0 angesehen werden, um in der Minterm- oder Maxterm-Methode Blöcke von Einsen oder Nullen zu vervollständigen. Ein gutes Beispiel dafür ist die Dekodierung von binär codierten Dezimalzahl (BCD). Hier spielen nur die Zahlen 0 bis 9 eine Rolle, die sogenannten Pseudotetraden dürfen ein beliebiges Ergebnis liefern, sind also Don’t-Care-Terme.

KV-Diagramm bei mehreren Ausgängen

Wenn eine Digitalschaltung mehrere Ausgänge hat, die Wahrheitstabelle also mehrere Ergebnisspalten hat, dann muss für jeden Ausgang ein eigenes KV-Diagramm erstellt werden.

Beispielsweise hat ein 1-aus-n-Decoder die nebenstehende Wahrheitstabelle und für seine 4 Ausgänge die 4 nebenstehenden 4 KV-Diagramme.

Bild 5-1: Wahrheitstabelle und KV-Diagramm für 1-aus-n-Decoder

Eingabe				Ausgabe
Zahl 1		Zahl 2		A < B	A = B	A > B
A1	A0	B1	B0	X	Y	Z
0	0	0	0	0	1	0
0	0	0	1	1	0	0
0	0	1	0	1	0	0
0	0	1	1	1	0	0
0	1	0	0	0	0	1
0	1	0	1	0	1	0
0	1	1	0	1	0	0
0	1	1	1	1	0	0
1	0	0	0	0	0	1
1	0	0	1	0	0	1
1	0	1	0	0	1	0
1	0	1	1	1	0	0
1	1	0	0	0	0	1
1	1	0	1	0	0	1
1	1	1	0	0	0	1
1	1	1	1	0	1	0

Ein weiteres Beispiel für mehrere Ausgänge ist ein ein 2+2-Bit-Vergleicher. Er hat 4 Eingangsvariablen und 3 Ausgangvariablen. Die Zahl A besteht aus 2 Bit (A₁ und A₀) und die Zahl B besteht aus 2 Bit (B₁ und B₀). Je nachdem, ob „A < B“, „A = B“ oder „A > B“ geben die drei Ausgänge (X, Y, Z) eine 1 oder 0 aus.

Die dazugehörige Wahrheitstabelle ist rechts. Die Bilder 5-2 bis 5-4 zeigen die 3 KV-Diagramme für die 3 Ausgänge.

Bild 5-2: Ausgang X

Bild 5-3: Ausgang Y

Bild 5-4: Ausgang Z

Normalformen

A	B	C	D	X
0	0	0	0	0
0	0	0	1	0
0	0	1	0	0
0	0	1	1	0
0	1	0	0	1
0	1	0	1	1
0	1	1	0	0
0	1	1	1	1
1	0	0	0	0
1	0	0	1	0
1	0	1	0	0
1	0	1	1	0
1	1	0	0	1
1	1	0	1	1
1	1	1	0	0
1	1	1	1	1

Üblicherweise werden Gruppen für die Einsen gebildet (Bild 6-2). Die Einsen leiten sich aus der Disjunktiven Normalform (DNF) ab. Es gibt aber auch die Möglichkeit Gruppen aus den Nullen zu bilden (in Bild 3 sind die Nullen nicht extra eingezeichnet, aber trotzdem vorhanden). Die Nullen stehen für die Konjunktive Normalform (KNF).

Die DNF lautet: ¬AB¬C¬D ∨ ¬AB¬CD ∨ ¬ABCD ∨ AB¬C¬D ∨ AB¬CD ∨ ABCD.

Die KNF lautet: (A∨B∨C∨D) ∧ (A∨B∨C∨¬D) ∧ (A∨B∨¬C∨D) ∧ (A∨B∨¬C∨¬D) ∧ (A∨¬B∨¬C∨D) ∧ (¬A∨B∨C∨D) ∧ (¬A∨B∨C∨¬D) ∧ (¬A∨B¬∨C∨D) ∧ (¬A∨B∨¬C∨¬D) ∧ (¬A∨¬B∨¬C∨D).

Die DNF wird aus der Tabelle ausgelesen, indem jede Zeile mit dem Ausgabewert „Eins“ aufgeschrieben wird. Die Eingangsvariablen für die eine Null steht, werden in negierter Form genommen. Alle Terme für die Zeilen (im vorliegenden Beispiel 6 Zeilen) werden durch „∨“ verbunden.

Für die KNF werden alle Zeilen mit dem Ausgabewert „Null“ rausgeschrieben, wobei Eingangsvariablen für die eine „Eins“ steht, in negierter Form genommen werden. Alle Terme für die Zeilen (im vorliegenden Beispiel 10 Zeilen) werden durch „∧“ verbunden, die Literale selber werden durch „∨“ verbunden.

Bild 6-1

Bild 6-2: Polynom BD ∨ B¬C¬D (Minimalpolynom: B (D ∨ ¬C¬D))

Bild 6-3: (¬C ∨ D) ∧ B

Kompakte Schreibweise

Eine kompakte Schreibweise für ein KV-Diagramm (Bild 7-1) zeigt folgendes Beispiel:
F = ∑ (0, 3, 6, 7, 10, 11, 12, 14, 15)

Ausgehend von einer durchgehenden Nummerierung (genauer gesagt: Indexierung – beginnend bei Feld 0) der Felder, wie in Bild 7-2 dargestellt, werden die Nummern der Felder aufgezählt, in denen eine Eins eingetragen ist.

Bild 7-1

Bild 7-2

Gesetzmäßigkeiten bei der Reduzierung

Durch die Zusammenfassung zu einer Gruppe der Größe 2ⁿ reduziert sich der logische Ausdruck um n Variablen. Das ist unabhängig davon, welche Lage oder Form die Gruppe hat oder ob sie über die Ränder hinwegreicht. Das ist auch unabhängig davon, ob es sich um ein 2x2, 2x4, 4x4 oder 4x4x4 KV-Diagramm handelt.

• Eine Achtergruppe (2³) reduziert sich um 3 Variablen (n = 3) – Bild 9-1.
• Eine Vierergruppe (2²) reduziert sich um 2 Variablen (n = 2) – Bild 9-2 und 9-3.
• Eine Zweiergruppe (2¹) reduziert sich um 1 Variable (n = 1) – Bild 9-4 und 9-5.
• Eine Einergruppe (2⁰) reduziert sich um Null Variablen (n = 0) – Bild 9-6.

Bild 9-1: Ergebnis: D

Bild 9-2: Ergebnis: CD

Bild 9-3: Ergebnis: B¬D

Bild 9-4: Ergebnis: AB¬C

Bild 9-5: Ergebnis: ¬B¬C¬D

Bild 9-6: Ergebnis: ¬ABCD

Regeln für die Gruppenbildung

• Benachbarte Felder in die eine Eins eingetragen ist, werden zu Gruppen zusammengefasst.
• Eine Gruppe darf keine Felder mit Nullen enthalten. (Oft werden die Nullen nicht mitgeschrieben und die Felder leer gelassen. In diesem Fall darf eine Gruppe keine leeren Felder enthalten.)
• Alle Einsen müssen in Gruppen zusammengefasst werden.
• Benachbarte Felder mit Einsen werden zu einer Gruppe zusammengefasst. (Felder, die sich an den Ecken berühren, diagonal, zählen nicht als benachbart.)
• Die Gruppen müssen so groß wie möglich sein.
• Es müssen so wenig Gruppen wie möglich gebildet werden.
• Die Gruppen dürfen nur Größen haben, die Zweierpotenzen entsprechen (1, 2, 4, 8, 16, 32, 64 …).
• Die Gruppen müssen rechteckige Blöcke sein.
• Die Gruppen dürfen sich überlappen.
• Die Gruppen dürfen über die Ränder hinweggehen.
• Zwei Gruppen dürfen nicht exakt die gleichen Einsen umfassen.
• Es darf keine Gruppe vollständig von einer anderen Gruppe umschlossen werden.

Zusammenfassung: Man sucht eine vollständige Überdeckung der Einsen mit möglichst großen rechteckigen Blöcken.

KV-Tafeln für 2 und 4 Variablen

Bild 1

Bild 2

Wer häufig mit dem KV-Diagramm arbeitet, wünscht sich eine Methode, ein KV-Diagramm schnell ausfüllen zu können.

Dies wird bei oben dargestellter Anordnung bei den vier Eingangsvariablen A, B, C und D durch folgende Anordnung erreicht:

Bild 3

Bild 4

Beispiele für Zusammenfassungen

• Bild 3: Verdeutlicht die logischen Werte der 16 Felder; wenn man aus einer Wahrheitstabelle zeilenweise die DNF in das KV-Diagramm überträgt, dann erfolgt die Eintragung in der Reihenfolge der roten Zahlen
• Bild 4: Die roten Zahlen erleichtern die zeilenweise Zuordnung der Wahrheitstabelle zu den einzelnen Feldern; die Reihenfolge hängt von der konkreten Beschriftung des KV-Diagramms ab; die Nummerierung stellt eine Arbeitserleichterung bei umfangreicher Verwendung von KV-Diagrammen dar

Dabei wird jedem Feld ihre Wertigkeit zugeordnet. Bei 4 Signalen sind dies 16 Einträge:

0000 = 0, 0001 = 1, 0010 = 2, …, 1110 = 14, 1111 = 15

Auf diese Weise kann das KV-Diagramm sehr schnell ausgefüllt werden. Es sind neben oben dargestellter Anordnungen aber auch Variationen der Anordnung der Eingangsvariablen A, B, C und D möglich. Dadurch ergeben sich andere Aufteilung der Wertigkeiten in der Matrix.

Beispiele

Lampe

Zu einer Lampe führen drei Schalter A, B und C, die entweder an (1) oder aus (0) sind. Folgende Tabelle zeigt, bei welcher Kombination von Schaltern die Lampe leuchtet (1) oder dunkel bleibt (0):

C	B	A	Lampe
0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	1
1	0	0	1
1	0	1	0
1	1	0	1
1	1	1	1

¬A ∨ B

Die disjunktive Normalform lautet also:
$l= \bar{A}\bar{B}\bar{C}\vee \bar{A}B\bar{C}\vee AB\bar{C}\vee \bar{A}\bar{B}C\vee \bar{A}BC\vee ABC$,
da die Minterme nur des Urbilds 1 gebildet werden (analog werden Maxterme nur des Urbilds 0 gebildet).
Die enthaltenen Konjunktionsterme sind gerade die Minterme.

Das dazugehörige KV-Diagramm sieht nun so aus:

¬A ∨ B

Nach der Minterm-Methode kann man im Diagramm nun zwei Viererblöcke bilden, die in einem Fall (grüne Gruppe) 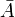$\bar A$ und im anderen Fall (blaue Gruppe) 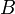$B\,$ enthalten. Die optimierte Funktion lautet demnach:
$l=\bar{A}\vee B$

Nach der Maxterm-Methode fasst man die beiden 0-Felder zu einem Zweierblock zusammen und erhält damit ohne weiteres $l=\bar{A}\vee B$

Das bedeutet, dass die Lampe l leuchtet, wenn der Schalter A ausgeschaltet oder der Schalter B eingeschaltet ist. Der Schalter C hat keine Wirkung.

Wechselschalter

Vorbetrachtung: Zuerst wird das zu lösende logische Problem mit Worten beschrieben. Es gibt die Schalter A und B, die als Wechselschaltung die Lampe L betätigen. Wenn beide Schalter in der Position 0 sind, dann ist die Lampe aus (Position 0) – Zeile 1 der Tabelle. Sind beide Schalter in der Position 1, dann ist die Lampe ebenfalls aus – Zeile 4. Ansonsten ist die Lampe an – Zeile 2 und 3. Alle weiteren Arbeitsschritte, einschließlich des erst weiter unten folgenden KV-Diagramms, können dann fast mechanisch erfolgen. Aus der logischen Problembeschreibung wird eine Wahrheitstabelle erstellt.

Schalter A	Schalter B	Lampe L
0	0	0
0	1	1
1	0	1
1	1	0

Aus den Zeilen der Wahrheitstabelle kann man direkt die Disjunktive Normalform (DNF) ablesen.

• Zeile 1: da das Ergebnis 0 ist (L = 0) wird keine Bedingung aus dieser Zeile geschrieben. Eine Bedingung wird nur geschrieben, wenn das Ergebnis 1 ist (L = 1).
• Zeile 2: ¬AB (Erklärung: wegen A=0 wurde ¬A geschrieben; für B=1 wurde B geschrieben)
• Zeile 3: A¬B (Erklärung: wegen A=1 wurde A geschrieben; für B=0 wurde ¬B geschrieben)
• Zeile 4: siehe Bemerkungen in Zeile 1

Bemerkung zu Zeile 2: Die Schreibweise ¬A ist gleichbedeutend mit 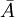$\bar{A}$ oder NICHT-A oder NOT-A oder A'. Außerdem wurde bei dieser Schreibweise das UND zwischen ¬A und B weggelassen. ¬AB ist also gleichbedeutend mit:

• ¬A AND B
• ¬A UND B
• ¬A ∧ B
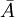• $\bar{A}$ ∧ B

Die Ausdrücke aus Zeile 2 und 3 werden noch mit einem ODER verbunden. So erhält man die Disjunktive Normalform (DNF) der in der Wahrheitstabelle dargestellten logischen Verknüpfung:

¬AB ∨ A¬B (Disjunktive Normalform)

Erst diese DNF ist der Ausgangspunkt für die Anwendung des Karnaugh-Veitch-Diagramms, das bisher noch nicht im Spiel war. Das Karnaugh-Veitch-Diagramm stellt lediglich einen Versuch dar, die Disjunktive Normalform weiter zu vereinfachen und zu kürzen. Selbst lange und große Ausdrücke lassen sich jedoch nicht immer weiter vereinfachen. Das lässt sich nicht abschätzen und stellt sich erst nach Anwendung des Karnaugh-Veitch-Diagramms heraus.

Bild 1

Bild 2

Bild 3

Bild 4

• Bild 1: Für 2 logische Variablen (A, B) wird ein leeres 2x2 KV-Diagramm benötigt. Jedes Feld im KV-Diagramm repräsentiert eine Zeile der Wahrheitstabelle.
• Bild 2: Es gibt 4 Felder, in die Eintragungen vorgenommen werden können (a, b, c, d)
• Bild 3: Den 4 leeren Feldern sind die hier (nur vorübergehend zur Veranschaulichung) eingetragenen logischen Werte zugeordnet (das UND Zeichen wurde wieder weggelassen: AB bedeutet A∧B usw.)
• Bild 4: In unserem konkreten Beispiel (siehe oben) wird für ¬AB eine 1 eingetragen (Feld b – oben rechts) und für A¬B eine 1 eingetragen (Feld c – unten links).

Aus Bild 4 ergibt sich, dass sich die eingesetzten Einsen nicht zu Gruppen zusammenfassen lassen. Folglich ist keine weitere Vereinfachung der DNF möglich. Im vorliegenden Fall ist die DNF der kürzeste logische Ausdruck (formale Bezeichnung: Minimalform = Minterm = Minimalterm) des Problems. Es sei nochmals daran erinnert, dass mit „1“ ausgefüllte Felder, die sich nur an ihren Ecken berühren nicht als Gruppe zusammengefasst werden. Bild 5 zeigt eine solche Gruppierung, die nicht zulässig ist.

Bild 5: keine erlaubte Gruppe

Bild 6

Bild 7

Bild 8

Bild 6 ist eine alternative Darstellung des 2x2 KV-Diagramms. Zu beachten ist, dass im vorliegenden Fall die Positionen von A und ¬A vertauscht sind, ebenfalls von B und ¬B. Üblicherweise lässt man das Eintragen der Nullen weg. Leere Felder werden also als 0 gelesen (Bild 7 und 8).

Identität von B

A	B	X
1	1	1
1	0	0
0	1	1
0	0	0

Die Wahrheitstabelle (rechts) stellt die Identität von B dar, das heißt die Ausgabe X ist identisch mit der Eingabe B. Aus der Tabelle leitet sich direkt die DNF ab: AB ∨ ¬AB. Dieser Term ist in Bild 9 in das KV-Diagramm eingetragen. Die linke „1“ steht für AB (aus der ersten Zeile der Wahrheitstabelle entnommen) und die rechte „1“ steht für ¬AB (aus der dritten Zeile der Wahrheitstabelle abgelesen). In Bild 10 ist dieser Term zu einer Gruppe zusammengefasst. Die Bedingungen sind erfüllt: 1.) benachbarte Felder und 2.) eine Gruppe aus 2 oder 4 Feldern. Das Wesentliche am KV-Diagramm, den man besser als KV-Algorithmus bezeichnen sollte, ist das Ableiten der Formel aus dieser Gruppe. Aus der Kenntnis, dass A ∨ ¬A = 1 ist, kann man A weglassen und es bleibt nur noch B übrig. Aus dem KV-Diagramm liest man die Lösung direkt ab: B. Das KV-Diagramm hat also gezeigt, dass AB ∨ ¬AB = B.

Bild 9

Bild 10

Bei diesem einfachen Beispiel könnte man das gleiche Ergebnis auch durch algebraische Umformung erreichen:
AB ∨ ¬AB = (A ∧ B) ∨ (¬A ∧ B) //Erklärung: UND-Symbol zur Veranschaulichung mitgeschrieben;
AB ∨ ¬AB = (A ∨ ¬A) ∧ B //Erklärung: B ausgeklammert (Distributivgesetz der Booleschen Algebra angewendet;
AB ∨ ¬AB = 1 ∧ B) //Erklärung: (A ∨ ¬A) durch 1 ersetzt, denn bekanntlich ist A ∨ ¬A = 1
AB ∨ ¬AB = B //Erklärung: denn 1 ∧ X = X (wie auch eine Überprüfung mittels Wahrheitstabelle beweist: 1∧W=W; 1∧F=F), – also kann man die 1 auch wegfallen lassen

Mit dem KV-Diagramm wurde faktisch das gleiche erreicht, jedoch auf graphische Art. Der Vorteil eines Diagramms ist, dass der Mensch Regelmäßigkeiten, also Muster bei einer bildlichen Darstellung viel einfacher erfassen kann (Mustererkennung), als bei abstrakten logischen Ausdrücken. Noch deutlicher wird der Unterschied zwischen bildlicher und abstrakter Mustererkennung bei 3, 4 oder 5 Variablen, wo das KV-Diagramm erst seine wirklichen Stärken ausspielen kann. Bei 6 Variablen versagt dann allerdings auch die Mustererkennung am KV-Diagramm, da es dafür keine geeigneten, einfachen KV-Diagramme gibt.

Negation von A

A	B	X
1	1	0
1	0	0
0	1	1
0	0	1

Die Wahrheitstabelle (rechts) stellt die Negation von A dar, das heißt die Ausgabe X ist identisch mit dem umgekehrten Signal der Eingabe A. Aus der Tabelle (Zeile 3 und 4) leitet sich direkt die DNF ab: ¬AB ∨ ¬A¬B. Dieser Term ist in Bild 11 in das KV-Diagramm eingetragen. Die rechte obere „1“ steht für ¬AB und die rechte untere „1“ steht für ¬A¬B. In Bild 12 ist dieser Term zu einer Gruppe zusammengefasst. Die Bedingungen sind erfüllt: 1.) benachbarte Felder und 2.) eine Gruppe aus 2 oder 4 Feldern. Jetzt kann aus dem KV-Diagramm und der umzeichneten Gruppe der Minterm abgeleitet werden.

Bild 11

Bild 12

Aus der Kenntnis, dass B ∨ ¬B = 1 ist, kann man B weglassen und es bleibt nur noch ¬A übrig – die Schreibweise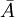 $\bar{A}$ ist identisch. Aus dem KV-Diagramm liest man die Lösung ¬A also direkt ab. Das KV-Diagramm hat also gezeigt, dass ¬AB ∨ ¬A¬B = ¬A.

Implikation von A auf B

A	B	X
1	1	1
1	0	0
0	1	1
0	0	1

Bild 1-1

Bild 1-2

Die Wahrheitstabelle (rechts) stellt die Implikation von A auf B. Aus der Tabelle (Zeile 1, 3 und 4) leitet sich direkt die DNF ab:
AB ∨ ¬AB ∨ ¬A¬B.
Dieser Term ist in Bild 1-1 in das KV-Diagramm eingetragen. Die linke obere „1“ steht für AB, die rechte obere „1“ steht für ¬AB und die rechte untere „1“ steht für ¬A¬B. In Bild 1-2 ist dieser Term zu zwei Gruppen zusammengefasst. Die Bedingungen sind erfüllt: 1.) benachbarte Felder und 2.) eine Gruppe aus 2 oder 4 Feldern. Jetzt kann aus dem KV-Diagramm und der umzeichneten Gruppe der Minterm abgeleitet werden.

Die rote (waagerechte) Gruppe wird zu B zusammengefasst, da A ∧ ¬A = 1. Die blaue (senkrechte) Gruppe wird zu ¬A vereinfacht, da B ∧ ¬B = 1.

Aus dem KV-Diagramm liest man die Lösung ¬A ∨ B also direkt ab. Das KV-Diagramm hat also gezeigt, dass
AB ∨ ¬AB ∨ ¬A¬B = ¬A ∨ B.
Damit wurde der Term durch Bearbeitung im KV-Diagramm wesentlich vereinfacht. Der Term ¬A ∨ B ist nicht weiter zu vereinfachen. Bei manchen Lösungen lässt sich nach dem KV-Diagramm noch eine Variable ausklammern. Das Zusammenfassen der drei Einsen zu einer einzigen Gruppe ist nicht erlaubt, da Gruppen nicht „um die Ecke“ gehen dürfen. Außerdem darf eine Gruppe nur 2 oder 4 Einsen enthalten.

Nach einer anderen, weniger verbreiteten Schreibweise schreibt man für UND (∧) einen Punkt, wie bei der Multiplikation (·), da sich der UND-Operator, beispielsweise beim Ausklammern wie eine Multiplikation verhält. Für ODER (∨) schreibt man ein Pluszeichen (+), da sich der ODER-Operator beispielsweise beim Ausklammern wie eine Addition verhält. Statt AB ∨ ¬AB ∨ ¬A¬B = ¬A ∨ B kann man also auch A·B + ¬A·B + ¬A·¬B = ¬A + B schreiben.

Tautologie

A	B	X
1	1	1
1	0	1
0	1	1
0	0	1

Diese Wahrheitstabelle (rechts) stellt eine Tautologie dar, die als Ausgabewert immer „1“ ergibt. Aus der Tabelle (Zeile 1, 2, 3 und 4) leitet sich direkt die DNF ab:
AB ∨ ¬AB ∨ A¬B ∨ ¬A¬B.
Dieser Term ist in Bild 2-1 in das KV-Diagramm eingetragen. Die linke obere „1“ steht für AB, die rechte obere „1“ steht für ¬AB, die linke untere „1“ steht für A¬B und die rechte untere „1“ steht für ¬A¬B. In Bild 2-2 ist dieser Term zu zwei Gruppen zusammengefasst. Die Bedingungen sind erfüllt: 1.) benachbarte Felder und 2.) eine Gruppe aus 2 oder 4 Feldern. Jetzt kann aus dem KV-Diagramm und der umzeichneten Gruppe der Minterm abgeleitet werden.

Die obere (grüne) Gruppe wird zu B zusammengefasst. Die untere (blaue) Gruppe wird zu ¬B zusammengefasst. Aus dem KV-Diagramm liest man die Lösung B ∨ ¬B ab. Allerdings kann man mittels algebraischer Umformung weiter vereinfachen: B ∨ ¬B = 1.

Bild 2-1

Bild 2-2

Bild 2-3

Korrekterweise hätte man gleich eine große Gruppe aus 4 Einsen bilden können (Bild 2-3). Und direkt die Lösung 1 ablesen können, denn A ∨ ¬A = 1 und B ∨ ¬B = 1

Drei logische Variablen

Für drei Variablen hat das KV-Diagramm 8 Felder. Zu beachten ist, dass die sich gegenüberliegenden Variablen (hier A und C) unterschiedlich angeordnet sind (Negation an unterschiedlicher Stelle), so dass sich für jedes der 8 Felder ein anderer logischer Ausdruck ergibt.

Bild 3-1

Bild 3-2

Zur Einsparung unnötiger Schreibarbeit kann das Eintragen der Nullen weggelassen werden.

Bild 3-3

Bild 3-4

Als Besonderheit kommt hier eine zyklische Eigenschaft des KV-Diagramms zum Vorschein. Die Gruppenbildung kann über den Rand hinweg zur anderen Seite fortgesetzt werden. In Bild 3-5 ist eine solche zulässige Gruppe markiert. Bild 3-6 veranschaulicht die zyklische Eigenschaft des KV-Diagramms.

Bild 3-5

Bild 3-6

Auch größere Gruppen, die über beide Ränder hinausreichen sind zulässig (Bild 3-7). Die beiden Zweiergruppen in Bild 3-8 sollten besser zu einer einzigen Vierergruppe zusammengefasst werden, um den kleinstmöglichen logischen Ausdruck als Lösung zu erhalten.

Bild 3-7

Bild 3-8

Allerdings sind auch weiterhin nur Gruppen mit einer bestimmten Größe zulässig. Die Größe muss eine Zweierpotenz sein: 2, 4, 8. Erst bei größeren KV-Diagrammen kommen 16 und 32 als Grenzen in betracht. Die in Bild 3-9 und 3-10 gezeigten Gruppen sind also nicht zulässig, da sie sechs Einsen umfasst.

Bild 3-9

Bild 3-10

Die unkorrekten Sechsergruppen aus Bild 3-9 und 3-10 müssen in kleinere Gruppen mit 2 und 4 Einsen aufgeteilt werden (Bild 3-11 und 3-12).

Bild 3-11

Bild 3-12

Bild 3-13 zeigt eine alternative Gruppenbildung zu Bild 3-12, die aber ebenso wie die Gruppenbildung bei Bild 3-11 leider nicht ganz korrekt ist. Bisher wurde eine zusätzlich Regel noch nicht weiter vertieft: „Die Gruppen müssen so groß wie möglich sein“. Nur so lässt sich eine maximale Minimierung erzielen. Bei Zuwiderhandlungen ist das Ergebnis jedoch nicht fehlerhaft, sondern nur nicht so stark minimiert.

Bild 3-13

Bild 3-14

Bild 3-15

Bild 3-16

Bild 3-17

Wie bei allen KV-Diagrammen sind Gruppen, die „um die Ecke“ gehen, nicht erlaubt. Die Gruppen in Bild 3-14, 3-15, 3-16 und 3-17 sind deshalb unzulässig.

Auch Bild 3-18 zeigt eine unkorrekte Gruppenbildung, da die rote Gruppe 3 Einsen umfasst. Korrekt ist dagegen die Gruppenbildung in Bild 3-19. Oft gibt es mehrere Möglichkeiten korrekte Gruppen zu bilden (Bild 3-20). Allerdings greift hier eine weitere, bisher noch nicht weiter vertiefte Regel: „Alle Einsen sind in Gruppen zusammenzufassen“. Die einzelne nicht erfasste Eins bildet also eine separate Gruppe (Bild 3-21). Jedoch greift eine weitere Regel: „Es sind so wenig Gruppen wie möglich zu bilden“. Nur so lässt sich eine maximale Reduzierung des logischen Ausdrucks erreichen. Die Regeln „Die Gruppen müssen so groß wie möglich sein“ und „Es sind so wenig Gruppen wie möglich zu bilden“ ergänzen sich oft und bewirken das gleiche – wenige und große Gruppen. Deshalb ist die Gruppierung in Bild 3-19 gegenüber 3-21 vorzuziehen, da in Bild 3-19 nur drei Gruppen gebildet werden müssen, während in Bild 3-21 vier Gruppen gebildet werden müssen.

Bild 3-18

Bild 3-19

Bild 3-20

Bild 3-21

In Bild 3-22 sind die 6 Einsen für folgenden, in DNF vorliegenden, Ausdruck eingetragen (von links nach rechts, erst die obere Zeile, dann die untere):
ABC ∨ AB¬C ∨ ¬ABC ∨ A¬BC ∨ A¬B¬C ∨ ¬A¬BC.
Daraus können zwei Gruppen gebildet werden. In der roten Gruppe heben sich B und ¬B auf, sowie C und ¬C, so dass nur A übrig bleibt. In der blauen Gruppe heben sich B und ¬B auf, so dass ¬AC bleibt. Die „rote“ und „blaue“ Teillösung ergeben zusammen den Term A ∨ ¬AC. Eine Vereinfachung zu einem Minterm A ∨ C ist durch Einbeziehung der 2 Einsen der linken Spalte in den blauen Block möglich (Bilder 3-22a).

Bild 3-22

Bild 3-22a

In Bild 3-23 ist der folgende Ausdruck in das KV-Diagramm eingetragen (untere Zeile von links nach rechts, dann obere Zeile):
A¬BC ∨ A¬B¬C ∨ ¬A¬B¬C ∨ ¬A¬BC ∨ ¬AB¬C.
Es können zwei Gruppen gebildet werden. Die blaue Gruppe vereinfacht man zu ¬B, da A (wegen A ∧ ¬A = 1) und C (wegen C ∧ ¬C = 1) wegfallen. Die rote Gruppe vereinfacht man zu ¬A¬C, da B (wegen B ∧ ¬B = 1) wegfällt. So erhält man als Minterm ¬B ∨ ¬A¬C.

Bild 3-23

Bild 3-24

Bild 3-25

Eine andere denkbare Lösung wäre, nur eine blaue Gruppe zu bilden und die rote Gruppe nicht zu bilden (Bild 3-24). Eine Regel gesagt aber: „Alle Einsen sind in Gruppen zusammenzufassen“ – also muss aus der einzelnen Eins auch noch eine Gruppe gebildet werden (Bild 3-25). Das verstieße aber gegen die Regel: „Die Gruppen müssen so groß wie möglich sein“. Deshalb ist die Bildung der Gruppen in Bild 3-23 die einzige richtige Lösung.

In Bild 3-26 bzw. 3-27 ist der folgende Ausdruck in das KV-Diagramm eingetragen (von links nach rechts, zuerst obere Zeile, dann untere Zeile):
AB¬C ∨ ¬AB¬C ∨ ¬ABC ∨ A¬B¬C ∨ ¬A¬B¬C ∨ ¬ABC.

Bild 3-26

Bild 3-27

Die in Bild 3-26 dargestellte Gruppenbildung ist nicht zulässig. Stattdessen werden, wie in Bild 3-27 gezeigt, 2 sich überlappende Gruppen gebildet. Die mittleren Einsen gehören zu beiden Gruppen. Die linke Gruppe (blau) vereinfacht sich zu ¬C und die rechte Gruppe (grün) zu ¬A. Als Minterm erhält man so die Lösung ¬C ∨ ¬A.

Bild 3-28

In Bild 3-28 ist der folgende Ausdruck in das KV-Diagramm eingetragen (von links nach rechts, zuerst obere Zeile, dann untere Zeile):
ABC ∨ AB¬C ∨ ¬AB¬C ∨ ¬A¬B¬C ∨ ¬A¬BC.
Die blaue Gruppe vereinfacht sich zu AB, die rote zu ¬A¬C und die grüne zu ¬A¬B, so dass man als Minterm AB ∨ ¬A¬C ∨ ¬A¬B erhält.

Bild 3-29

In Bild 3-29 ist der Ausdruck A¬BC ∨ ¬A¬BC eingetragen. Wegen der zyklischen Eigenschaft des KV-Diagramms lässt sich eine Gruppe bilden, die über die Ränder hinausreicht und die dann zu ¬BC vereinfacht werden kann.

Bild 3-30: ABC ∨ ¬ABC ∨ A¬BC ∨ ¬A¬BC vereinfacht sich zu C.
In Bild 3-31 wird gegen die Regel „Die Gruppen müssen so groß wie möglich sein“ verstoßen. Trotzdem wird der dazugehörige logische Term zu Demonstrationszwecken hier angeführt: ABC ∨ ¬ABC ∨ A¬BC ∨ ¬A¬BC vereinfacht sich zu AC (rote Gruppe) und ¬AC (grüne Gruppe). Lösung: AC ∨ ¬AC. Durch Ausklammern von C erhält man C ∧ (A ∨ ¬A). Das ist identisch mit C ∧ 1 und somit identisch mit C. Diese Lösung ist bereits aus Bild 3-30 bekannt. Dort wurde sie allerdings ohne zusätzliche algebraische Umformung erreicht.

Bild 3-30

Bild 3-31

Nicht immer ist ersichtlich, ob sich ein Ausdruck weiter kürzen lässt. Erst das Eintragen der Einsen schafft in manchen Fällen Gewissheit, dass keine Gruppen gebildet werden können. Obwohl man gerade bei langen Ausdrücken vermutet, dass sie gekürzt werden können.

In Bild 3-32 ist folgende DNF eingetragen:
AB ¬C ∨ A ¬BC ∨ ¬ABC ∨ ¬A ¬B ¬C
Da sich die Felder mit den Einsen nur an den Ecken berühren, können nur Gruppen mit je einem Feld gebildet werden (Bild 3-33). In diesem Fall lässt sich der Term nicht weiter kürzen. Die DNF ist auch gleichzeitig der Minterm.

Bild 3-32

Bild 3-33

Bild 3-33 zeigt eine andere mögliche Darstellung für ein KV-Diagramm mit 3 Variablen.

Bild 3-33

Vier logische Variablen

Bei vier logischen Variblen benötigt das KV-Diagramm 16 Felder (Bild 4-1). Auf jede Seite des Diagramms schreibt man je eine Variable – jeweils in normaler und verneinter Form. Die Reihenfolge von verneinter und normaler Form ist so zu wählen, dass sich für jedes Feld ein anderer logischer Wert ergibt (zur Veranschaulichung in Bild 4-2 eingetragen) und so, dass sich von Nachbarfeld zu Nachbarfeld jeweils nur die Negation einer einzigen Variable ändert. Beispielsweise ist die direkte Nachbarschaft von AB und ¬A¬B nicht erlaubt, während auf AB die Kombination ¬AB folgen darf. Natürlich muss jede mögliche Variablenkombination genau ein mal in den 16 Feldern vertreten sein. Einzelheiten dazu siehe unter Gray-Code.

Bild 4-1

Bild 4-2

Es gibt mehrere Möglichkeiten die Variablen und ihre Verneinung am Rand des Feldes einzutragen (Bild 4-3 und 4-4).

Bild 4-3

Bild 4-4

Bild 4-5

Eine andere Möglichkeit der Beschriftung der Felder ist in Bild 4-5 dargestellt. Das ist die von Karnaugh eingeführte Version des Diagramms. Während die Version von Veitch in den Bildern 4-1, 4-3 und 4-4 zu sehen ist. In der Version von Karnaugh ist der Gray-Code, der beiden Versionen zu Grunde liegt, wesentlich klarer zu erkennen.

Die Bilder 4-6 bis 4-8 demonstrieren den logischen Zusammenhang zwischen der Diagrammversion von Veitch und der Version von Karnaugh.

Bild 4-6

Bild 4-7

Bild 4-8

Eine weitere gebräuchliche Version des 4x4-Diagramms zeigt Bild 4-9. Die dicken Striche dienen für die Markierung der nicht verneinten Variablen. Bild 4-10 verdeutlicht nochmals die Belegung der Variablen. Diese ausführliche Schreibweise in Bild 4-10 entfällt aber in der praktischen Anwendung dieser Diagrammart. Statt der Variablen A, B, C und D für die Eingabevariablen sind auch indizierte Variablen (X₀, X₁, X₂, X₃) gebräuchlich (Bild 4-11).

Bild 4-9

Bild 4-10

Bild 4-11

Wie bereits bei den KV-Diagrammen mit drei Variablen sind auch hier Gruppen erlaubt, die den Rand überschreiten. Egal, ob in horizontaler (rot) oder vertikaler (grün) Richtung – Bild 4-12. Die zyklische Eigenschaft des KV-Diagramms sowohl horizontal (Bild 4-13) als auch vertikal (Bild 4-14) beruht auf dem Gray-Code, der speziell für das KV-Diagramm ausgewählt wurde.

Bild 4-12

Bild 4-13

Dieses zyklische Verhalten des KV-Diagramms in horizontaler und gleichzeitig in vertikaler Richtung (in Bild 4-13 und 4-14 nur getrennt wiedergegeben) wird als toroidal bezeichnet, da ein Torus (Bild 4-15) diese Eigenschaft hat. Ein KV-Diagramm ist ein flacher Torus (Bild 4-15a). Das zweidimensionale KV-Diagramm kann durch Faltung und Krümmung in den dreidimensionalen Torus umgewandelt werden. Dazu wird das rechteckige KV-Diagramm zu einem waagrechten Schlauch gebogen und der Schlauch dann zu einem Ring geschlossen.

Bild 4-14

Bild 4-15: Torus

Bild 4-15a: Diese Fläche umschließt den Torus in Bild 4-15

Da das KV-Diagramm sich sowohl horizontal als auch vertikal zyklisch verhält (Torus), ist beim 4x4 Diagramm auch eine besondere Gruppenbildung an den Ecken möglich und erlaubt – Bild 4-16. Eine Grundbedingung ist aber immer, dass die Größe der Gruppe einer Zweierpotenz entspricht – 2, 4, 8, 16. Deshalb ist die Gruppe in Bild 4-17 (6 Felder) und Bild 4-18 verboten.

Bild 4-16: Die Gruppenbildung "über die Ecken" ist am Torus in Bild 4-15 und 4-15a anschaulich dargestellt

Bild 4-17

Bild 4-18

Bild 4-19

Bild 4-20

Genaugenommen liegt bereits beim 2x2 KV-Diagramm die gleiche zyklische Eigenschaft vor wie beim 4x4-Diagramm. Man macht nur keinen Gebrauch davon. Die Zweiergruppe in Bild 4-19 könnte man genauso gut zu beiden Seiten über die Ränder ausdehnen und dafür zwischen beiden Einserfeldern die Verbindung in der Mitte unterbrechen (Bild 4-20).

Bild 4-21

Bild 4-22

Auch die Vierergruppe in Bild 4-21 könnte man in Analogie zu Bild 4-16 so zeichnen, das sie sowohl horizontal als auch vertikal zyklisch über die Ränder geht. Dafür könnte man dann die Verbindung der Gruppe auf der „Vorderseite“ des KV-Diagramms unterbrechen, also die Gruppe sowohl horizontal, als auch vertikal aufspalten (Bild 4-24).

Bild 4-23 zeigt nochmals zyklische Eigenschaften eines 2x2-Diagramms, für deren Nutzung jedoch in der Praxis kein Bedarf besteht, da die Gruppen im Bild 4-24 ausreichen. Auch beim 2x4-Diagramm trifft man die gleichen zyklischen Eigenschaften (Bild 4-25), die jedoch in der Praxis nur in horizontaler Richtung genutzt werden (rote Gruppe), während die vertikale Gruppe (blau) ohne praktische Bedeutung ist.

Bild 4-23

Bild 4-24

Bild 4-25

Bild 4-26

Bild 4-26 (links oben beginnend, reihenweise von links nach rechts) – die gegebene DNF lautet:
ABCD ∨ AB¬CD ∨ ¬AB¬CD ∨ A¬BC¬D ∨ ¬A¬BC¬D ∨ ¬A¬B¬CD.
Sie vereinfacht sich zu:

• blaue Gruppe: ABD (weil sich C mit ¬C zu 1 aufhebt und wegfallen kann);
• grüne Gruppe: ¬A¬CD (weil sich B mit ¬B zu 1 aufhebt und wegfallen kann);
• rote Gruppe: ¬BC¬D (weil sich A mit ¬A zu 1 aufhebt und wegfallen kann).
  

Das Endergebnis ist folglich: ABD ∨ ¬A¬CD ∨ ¬BC¬D.

Bild 4-27

Bild 4-27 (links oben beginnend, reihenweise von links nach rechts) – die gegebene DNF lautet:
ABCD ∨ ¬ABCD ∨ A¬BCD ∨ ¬A¬BCD.
Da sich eine gültige Gruppe bilden lässt, in der sich A und B jeweils mit ihrer negierten Form aufheben, lautet das vereinfachte Ergebnis: CD.

Bild 4-28

Bild 4-29

Bild 4-28 zeigt das KV-Diagramm mit der eingetragenen DNF (zeilenweise, von links oben beginnend):
ABCD ∨ AB¬CD ∨ ¬AB¬CD ∨ ¬ABCD ∨ ABC¬D ∨ AB¬C¬D ∨ ¬AB¬C¬D ∨ ¬ABC¬D ∨ A¬BC¬D ∨ A¬B¬C¬D ∨ ¬A¬B¬C¬D ∨ ¬A¬BC¬D.
Hier könnte man ohne KV-Diagramm schnell den Überblick verlieren. Die eingezeichnet Gruppe (Bild 4-32) ist so nicht zulässig (12 Felder). Bild 4-29 zeigt die korrekte Bildung der Gruppen (Achtergruppe – also eine Zweierpotenz, so groß wie möglich, so wenig Gruppen wie möglich). Die obere Gruppe (grün) vereinfacht sich zu: B. Die untere Gruppe (rot) vereinfacht sich zu: ¬D. Somit lautet der Minterm: B ∨ ¬D.

Bild 4-30

Bild 4-31

Nicht den Regeln entsprechend (so große Gruppen wie möglich, so wenig Gruppen wie möglich) ist die Gruppenbildung in Bild 4-30 und 4-31.

A	B	C	D	X
0	0	0	0	0
0	0	0	1	0
0	0	1	0	0
0	0	1	1	0
0	1	0	0	1
0	1	0	1	0
0	1	1	0	0
0	1	1	1	0
1	0	0	0	1
1	0	0	1	1
1	0	1	0	1
1	0	1	1	1
1	1	0	0	1
1	1	0	1	0
1	1	1	0	1
1	1	1	1	1

Bild 4-32

In Bild 4-32 liegt die Variante der Beschriftung nach Karnaugh vor, bei der man den Gray-Code besser erkennt. Bei dieser Art der Randbeschriftung kann man aus einer gegebenen Wahrheitstabelle direkt die Werte in das KV-Diagramm eintragen. Das Aufschreiben der DNF kann entfallen und auch das Übertragen der DNF in die Tabelle. Beides sind potentielle Fehlerquellen, die so entfallen.

Bild 4-33

Die gegebene Wahrheitwertetabelle (rechts) kann direkt in das 4x4-Diagramm übertragen werden (Bild 4-33). Der Umweg über die DNF kann entfallen. Sie wird hier nur nochmals zur Demonstration der enormen Arbeitserleichterung gegenüber der Beschriftungsversion von Veitch wiedergegeben:
¬AB¬C¬D ∨ A¬B¬C¬D ∨ A¬B¬CD ∨ A¬BC¬D ∨ A¬BCD ∨ AB¬C¬D ∨ ABC¬D ∨ ABCD.
Allerdings kann man sich auch mit dieser Diagrammversion nicht die nachfolgende Arbeit ersparen: Gruppen bilden und Ergebnis ablesen. Das Ablesen gestaltet sich bei dieser Beschriftungsart sogar schwieriger:

• rote Gruppe: AC;
• blaue Gruppe: B¬C¬D;
• grüne Gruppe: A¬B.

Das Endergebnis lautet: AC ∨ B¬C¬D ∨ A¬B.

A	B	C	D	X
0	0	0	0	0
0	0	0	1	1
0	0	1	0	0
0	0	1	1	0
0	1	0	0	1
0	1	0	1	1
0	1	1	0	1
0	1	1	1	1
1	0	0	0	1
1	0	0	1	1
1	0	1	0	0
1	0	1	1	0
1	1	0	0	0
1	1	0	1	0
1	1	1	0	0
1	1	1	1	0

Bild 4-34

Bild 4-35

Bild 4-36

Bild 4-37

Die Forderung die Gruppen so groß wie möglich zu gestalten und so wenig wie möglich Gruppen zu verwenden, lässt bei den Versionen in Bild 4-34 bis 4-37 nur die zwei Gruppen in Bild 4-35 als optimale Wahl zu. Ausgangspunkt ist die Wahrheitstabelle (rechts). Die dazugehörige DNF lautet:
¬A¬B¬CD ∨ ¬AB¬C¬D ∨ ¬AB¬CD ∨ ¬ABC¬D ∨ ¬ABCD ∨ A¬B¬C¬D ∨ A¬B¬CD.
Die obere Gruppe (grün, Bild 4-35) reduziert sich zu ¬AB. Die untere Gruppe (rot) reduziert sich zu ¬B¬C.
Das Endergebnis lautet:¬AB ∨ ¬B¬C.

Bild 4-38

Bild 4-39

Für die drei Einserfelder in Bild 4-38 kommen nur die in Bild 4-39 dargestellten Gruppen in Betracht. Die DNF lautet:
¬ABCD ∨ A¬BCD ∨ ¬A¬BCD.
Die rote Gruppe reduziert sich zu ¬BCD. Die blaue Gruppe reduziert sich zu ¬ACD.
Das Endergebnis lautet:¬BCD ∨ ¬ACD.

Bild 4-40

Bild 4-41

Für das Minimierungsproblem in Bild 4-40 erweisen sich die in Bild 4-41 dargestellten Gruppen als optimal. Die DNF lautet:
ABCD ∨ ¬ABCD ∨ A¬BCD ∨ ¬AB¬C¬D ∨ ¬ABC¬D ∨ ¬A¬B¬C¬D ∨ ¬A¬BC¬D ∨ ¬A¬B¬CD ∨ ¬AB¬CD.
Die rote Gruppe reduziert sich zu CD. Die blaue Gruppe reduziert sich zu ¬A¬B. Die grüne Gruppe reduziert sich zu ¬A¬D.
Das Endergebnis lautet:CD ∨ ¬A¬B ∨ ¬A¬D.

Bild 4-42

Bild 4-43

Für die Aufgabenstellung in Bild 4-42 ist die Gruppenbildung in Bild 4-43 am Besten. Während die Gruppen in Bild 4-44 bis 4-46 nicht die Forderungen erfüllen: „Die Gruppen müssen so groß wie möglich sein“ und „Es sind so wenig Gruppen wie möglich zu bilden“.

Bild 4-44

Bild 4-45

Bild 4-46

Für die Aufgabenstellung in Bild 4-47 ist die Gruppenbildung in Bild 4-48 am besten. Während die Gruppen in Bild 4-49 zu klein sind.

Bild 4-47

Bild 4-48

Bild 4-49

Bild 4-50

Bild 4-50 zeigt eine weitere Möglichkeit KV-Diagramme mit 4 Variablen darzustellen.

Die Bilder 4-51 bis 4-58 zeigen weitere Möglichkeiten Gruppen zu bilden.

Bild 4-51

Bild 4-52

Bild 4-53

Bild 4-54

Bild 4-55

Bild 4-56

Bild 4-57

Bild 4-58

Fünf logische Variablen

Bild 5-1

Bild 5-2

Das KV-Diagramm für fünf logische Variblen benötigt 32 Felder. Bildlich kann man sich das als zwei übereinandergelegte 4x4-KV-Diagramme vorstellen (Bild 5-1). Dabei steht eine Schicht (rot) für die normale (nicht negierte) fünfte Variable (E) und die andere Schicht (blau) für die negierte fünfte Variable (¬E). Für die Eintragungen der Einsen kommt keine prinzipiell neue Regel dazu. Das KV-Diagramm besteht aus 32 Feldern. Die größte erlaubte Gruppe darf 32 Felder umschließen.

Jetzt können auch zwei Felder (hier als Würfel dargestellt) zu einer Gruppe zusammengefasst werden, die übereinander liegen (Bild 5-2).

Bild 5-3

Bild 5-4

Analog können auch noch größere übereinanderliegende Gruppen gebildet werden. In Bild 5-3 ist nicht klar ersichtlich, ob unter den beiden nebeneianderliegenden Einsen in der roten Schicht auch je eine Eins in der blauen Schicht steht. Wenn das der Fall wäre, dann könnte man aus ihnen eine Vierergruppe bilden.

Auch die zyklischen Eigenschaften bleiben erhalten. Weil sie sich aber auf eine weitere Variable beziehen sind sie nicht mehr so anschaulich. Bild 5-4 zeigt vier Einserfelder (als Würfel dargestellt) in der roten Schicht und genau darunter liegend vier weitere Einserfelder in der blauen Schicht. Diese 8 Würfel (Felder) lassen sich zu einer Achtergruppe zusammenfassen.

Bild 5-5

Bild 5-6

Für fünf Variablen werden für das Arbeiten mit dem KV-Diagramm zwei 4x4-Diagramme nebeneindergezeichnet. Bild 5-5 zeigt die obere Schicht (rot) und Bild 5-6 die untere (blau). Die dreidimensionale Abbildung (Bild 5-1) diente nur zur Veranschaulichung.

Zusätzlich zum „normalen“ Erkennen der zulässigen Gruppen muss jetzt auch noch die Gruppenbildung über beide Ebenen hinweg erkannt werden. So zeigt das zu Bild 5-7 gehörende KV-Diagramm (Bild 5-8 zusammen mit Bild 5-9) eine blaue Vierergruppe und eine rote Zweiergruppe, die jeweils über beide Ebenen gehen.

Bild 5-7: räumliche Darstellung von Bild 5-8 und 5-9

Bild 5-8

Bild 5-9

Bild 5-8 zusammen mit Bild 5-9 zeigt das KV-Diagramm mit der eingetragenen DNF:
ABC¬DE ∨ AB¬C¬DE ∨ ¬A¬B¬C¬DE ∨ ABC¬D¬E ∨ AB¬C¬D¬E ∨ ¬A¬B¬C¬D¬E.
Die blaue Vierergruppe vereinfacht sich zu: AB¬D (C und E liegen gleichzeitig auch in negierter Form in der Grupep vor und entfallen; für E und ¬E muss man sich die beiden Ebenen gedanklich übereinander projizieren).
Die rote Zweiergruppe vereinfacht sich zu: ¬A¬B¬C¬D (E entfällt).
Das Endergebnis lautet folglich: AB¬D ∨ ¬A¬B¬C¬D.

Bild 5-10

Bild 5-10 zeigt die DNF:
ABCDE ∨ ¬ABCDE ∨ A¬BCDE ∨ ¬A¬BCDE ∨ ABCD¬E ∨ ¬ABCD¬E ∨ A¬BCD¬E ∨ ¬A¬BCD¬E.
Die Achtergruppe reduziert sich zu: CD.
(Anmerkung: die Flächen der Würfel sind hier zu Illustrationszwecken mit mehreren Einsen beschriftet. Da in dieser Darstellung ein Würfel einer Fläche im 4x4 Diagramm gleichzusetzen ist, gilt je Würfel nur eine Eins. Diese kann man sich gedanklich in den Würfel hineinnprojezieren. Beim Würfel hinten links wird angenommen, dass in der darunterliegenden blauen Schicht auch eine Eins steht, auch wenn sie nicht im Bild sichtbar ist.)

Bild 5-11

Bild 5-12

Eine andere Möglichkeit der räumlichen Darstellung von KV-Diagrammen mit 5 Variablen ist in Bild 5-11 dargestellt. In Bild 5-12 sind die gleichen Felder belegt, wie in Bild 5-7 bis 5-9.

Bild 5-13

Bild 5-14

Eine weitere Möglichkeit für die graphische Darstellung eines KV-Diagramms für 5 Variablen zeigt Bild 5-13 und Bild 5-14.

Bild 5-15: ¬A¬BE ∨ A¬BDE

Bild 5-15 zeigt eine weitere Version des KV-Diagramms für 5 Variablen. Dabei besteht zwischen den beiden 4x4 Blöcken eine Spiegelachse – gestrichelte Linie. In dieser Version ist die Zugehörigkeit zu den Gruppen, die sich über beide Seiten erstrecken, nur bei symmetrischer Anordnung um die Spiegelachse gegeben.

Sowohl die seitliche Beschriftung (AB), als auch obere Beschriftung (für CDE) ist in Gray-Code. Gray-code hat die Eigenschaft symmetrisch zu sein.

Sechs logische Variablen

Bild 6-1

Das KV-Diagramm für sechs logische Variblen benötigt 64 Felder – in Bild 6-1 dreidimensional als Würfel dargestellt.

Bild 6-2

Bild 6-3

Bild 6-4

Bild 6-5

Auch hier wird für die praktische Anwendung jede Ebene als separates 4x4-Diagramm gezeichnet. Die Gruppenbildung über die Ebenen hinweg bedarf noch größerer Aufmerksamkeit. Die Handhabung der zyklischen Eigenschaften entzieht sich bei sechs Variablen schon fast dem Vorstellungsvermögen. Zu beachten ist, dass die fünfte und sechste Variable (also die dritte Dimension) ebenfalls nach dem Gray-Code angeordnet sind, damit jedes Feld einen anderen, und nur jeweils um eine Stelle verschiedenen Wert hat.

Bild 6-6

Bild 6-7

Eine andere Möglichkeit der räumlichen Darstellung von KV-Diagrammen mit 6 Variablen ist in Bild 6-6 dargestellt. In Bild 6-7 wurde ein Beispiel für die Belegung der Felder dargestellt.

Bild 6-8 zeigt eine mögliche Version eines ausgefüllten KV-Diagramms mit 6 Variablen. In Bild 6-9 sind die 4 Felder jeweils um eine vertikale und horizontale Mittelachse gespiegelt. (Anmerkung: die Randbeschriftungen sind in den vorliegenden Bildern nicht identisch – Bild 6-5, 6-7, 6-8; es handelt sich also um unterschiedliche logische Ausdrücke)

Bild 6-8

Bild 6-9

Aus Bild 6-8 kann man folgende Lösung ablesen:

 A B | C D | E F
-------------
 0 0 | 0 1 | – – (blau)
 1 – | 1 – | – 1 (grün)
 0 1 | – – | 1 – (rot)

Lösung: ¬A¬B¬CD ∨ ACF ∨ ¬ABE

Beispiel für Don’t-Care-Zustände

Don’t-Care-Zustände (ungebräuchliche deutsche Übersetzung: Egal-Zustände) sind Ergebnisse, die egal sind. Beispielsweise handelt es sich um Zeilen in der Wahrheitstabelle, für die keine Eingaben vorgesehen sind und folglich auch keine Ausgaben berücksichtigt werden wollen. Sie werden als „X“ in das KV-Diagramm eingetragen und dürfen für den Zweck der Gruppenbildung als „1“ oder „0“ betrachtet werden. Die Wahl erfolgt so, dass sich besonders günstig Gruppen bilden lassen (wenig Gruppen, große Gruppen).

Bild 7-1 zeigt zwei Don’t-Care-Zustände (blau umrahmt, aber keine Gruppe). Bild 7-2 zeigt eine fast optimale Gruppenbildung mit diesen Don’t-Care-Zuständen. Zu diesem Zweck wurde das rechte „X“ wie eine „1“ behandelt und das linke „X“ wie eine „0“. Werden beide „X“ auch noch in den roten Block einbezogen, und dieser zum 4er-Block erweitert, ist die Blockbildung optimal (Bild 7-2a).

Bild 7-1

Bild 7-2

Bild 7-2 a

Bild 7-3

Ohne diese Don’t-Care-Zustände wäre die Gruppenbildung ungünstiger (Bild 7-3).

Die Variante in Bild 7-4 ist nicht optimal, da die blaue Gruppe größer sein könnte.
Die Variante in Bild 7-5 ist nicht optimal, da die Don’t-Care-Zustände nicht genutzt werden und die blaue Gruppe größer sein könnte.
Die Variante in Bild 7-6 ist nicht optimal, da die Don’t-Care-Zustände nicht genutzt werden.

Bild 7-4

Bild 7-5

Bild 7-6

Bild 7-7

Bild 7-8

Für das Problem in Bild 7-7 erweist sich die Gruppenbildung in Bild 7-8 als optimal. Die rote Gruppe reduziert sich zu CD und die blaue Gruppe zu ¬B¬C¬D.
Das Endergebnis lautet:CD ∨ ¬B¬C¬D.

Bild 7-9

Bild 7-10

Für das Minimierungsproblem in Bild 7-9 erweisen sich die in Bild 7-10 dargestellten Gruppen als optimal.
Die rote Gruppe reduziert sich zu C¬D. Die blaue Gruppe reduziert sich zu B¬C. Die grüne Gruppe reduziert sich zu ¬CD.
Das Endergebnis lautet:C¬D ∨ B¬C ∨ ¬CD.

Bild 7-11

Bild 7-12

Weitere Beispiel für Gruppenbildungen mit vorgegebenen Don’t-Care-Zuständen zeigen Bild 7-11 und 7-12. Hier wurden die Don’t-Care-Zustände mit einem Bindestrich statt mit einem „X“ gekennzeichnet. Beide KV-Diagramm sind identisch, nur die Gruppenbildung unterscheidet sich.

Bild 7-13

Bild 7-14

Bild 7-15

Ein weiteres Beispiel zeigt Bild 7-13. Die Gruppenbildung in Bild 7-14 ist nicht optimal, da die Gruppen kleiner als möglich sind. Besser ist die Wahl der Gruppe in Bild 7-15.

Beispiel für Race hazards

A	B	C	Z
0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	0
1	1	1	0

Race hazards (Glitch) in kombinatorischen Schaltungen führen nicht unbedingt zu Fehlfunktionen. Kritisch kann ihr Auftreten aber bei synchronen sequentiellen Schaltungen sein, z. B. bei Flipflops und Zustandsmaschinen. Im KV-Diagramm lassen sich Race hazards sehr leicht erkennen. Sie treten beim Übergang von einer Gruppe zur anderen Gruppe auf. Wegen Race hazards nimmt man in digitalen Schaltungen manchmal nicht die mit dem KV-diagramm gefundene minimale Form des logischen Ausdrucks.

Bild 8-1 zeigt das zur Wahrheitstabelle (rechts) gehörende KV-Diagramm. Beim Übergang vom Feld mit der blauen Eins zum Feld mit der grünen Eins kann ein Race hazard auftreten (Bild 8-1). Zur Vermeidung des Race hazards wird ein weiterer Minterm hinzugefügt (rote Gruppe), der die beiden isolierten Minterme (grüne und blaue Gruppe) verbindet (Bild 8-2). Diese rote Gruppe fügt zwar redundante Logik hinzu, verhindert aber Race hazards. Bei der redundanten Gruppe handelt es sich um eine redundante Primkonjunktion. Aus der Minimallösung A¬B ∨ ¬A¬C wird durch Hinzufügen der Gruppe zur Verhinderung des Race hazards der nicht mehr minimale Term A¬B ∨ ¬A¬C ∨ ¬B¬C

Bild 8-1

Bild 8-2

Bild 8-3: AB ∨ ¬AC

Bild 8-4: AB ∨ ¬AC ∨ BC

Etwas schwieriger sind Race hazards zu erkennen, wenn sie am Rand des KV-Diagramms auftreten. Beim Übergang von der blauen zur grünen Eins (Bild 8-3), natürlich auch in umgekehrter Richtung, kann ein Race hazard auftreten, der auch hier durch eine zusätzliche Gruppe (rot) verhindert werden kann (Bild 8-4). Aus der Minimallösung AB ∨ ¬AC wird dann AB ∨ ¬AC ∨ BC.

Bild 8-5: AB ∨ ¬AC

Bild 8-6: AB ∨ ¬AC ∨ BC

Die zu Bild 8-3 bzw. 8-4 dazugehörigen Logikschaltungen sind in Bild 8-5 bzw. 8-6 zu sehen.

A	B	C	Z
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	1

Der in Bild 8-5 drohende Race hazard ist in den Bildern 8-7 bis 8-9 illustriert. In Bild 8-7 liegt an A, B und C der logische Wert Eins an – durch rote Leitungen illustriert (schwarze Leitungen für den Wert Null) – letzte Zeile der Wahrheitstabelle (blaue Eins). Es ergibt sich der Ausgangswert Z = 1. In Bild 8-8 tritt der Race hazard auf, beim Umschalten von A = 1 auf A =0, beim Umschalten von Zeile 8 (blaue Eins) auf Zeile 4 (grüne Eins). Das Ergebnis sollte laut Tabelle und KV-Diagramm Eins sein, ist aber kurzzeitig Null, ein Glitch – eine kurzzeitige Falschaussage – ein Race hazard. Das falsche Ergebnis (Bild 8-8) dauert nur einen Sekundenbrauchteil an. Das richtige logische Ergebnis (Bild 8-9) folgt erst nach diesem Sekundenbruchteil. Die dazugehörige Tabelle steht rechts. Ursache für den Glitch ist die notwendige Schaltzeit für die Negation – im Inverter.

Bild 8-7: A=1, B=1, C=1, Z=1

Bild 8-8: Glitch A=0, B=1, C=1, Z=0

Bild 8-9: A=0, B=1, C=1, Z=1

Bild 8-10

Bild 8-11

Ein weiteres Beispiel für Race hazards sind die drei Gruppen in Bild 8-10. Hier kann ein Race hazard sowohl beim Übergang von der roten zur blauen Eins auftreten (mit grüner Brücke hervorgeheoben), als auch beim Übergang von der roten zur grünen Eins (mit roten Punkten hervorgehoben). Verhindert werden diese Race hazards durch Hinzufügen der gelben Gruppe (Bild 8-11), die alle drei Gruppen überlappt.

XNOR und XOR

Bild 1

Bild 2: XNOR

Bild 3: XOR

Die XNOR-Verknüpfung und die XOR-Verknüpfung sind im KV-Diagramm durch diagonale Einzelfelder gekennzeichnet und können nicht weiter vereinfacht werden.

Mengendiagramm

Das Karnaugh-Veitch-Diagramm ist eine abgewandelte, abstrakte Form des Mengendiagramms (Venn-Diagramm).

Die Bilder 1 bis 4 zeigen ein Venn-Diagramm und das äquivalente KV-Diagramm.

2 Variablen

Bild 1: KV-Diagramm

Bild 2: Venn-Diagramm

4 Variablen

Bild 3: KV-Diagramm

Bild 4: Venn-Diagramm

Die Bilder 5 bis 8 zeigen noch einmal die einzelnen Teilmengen, aus denen sich das Venn-Diagramm in Bild 4 zusammensetzt.

4 Variablen

Bild 5: Venn-Diagramm	Bild 6: Venn-Diagramm
Bild 7: Venn-Diagramm	Bild 8: Venn-Diagramm

Siehe auch

• Verfahren nach Quine und McCluskey – bei mehr als 5 Eingangsvariablen besser geeignet, als das KV-Diagramm
• Pseudotetraden
• Schaltalgebra
• Karnaugh-Diagramme (oben), wegen der gleichen Aussprache der Personennamen, nicht mit den Diagrammen des Carnot-Kreisprozesses verwechselen

Literatur

• Maurice Karnaugh: The Map Method for Synthesis of Combinational Logic Circuits, Transactions of the AIEE, Vol. 72, No. 9 (1953), 593–599.
• Edward W. Veitch: A chart method for simplifying truth functions, Mai 1952, Proc. Assoc. for Computing Machinery, Pittsburgh, 127–133.
• Klaus Beuth: Digitaltechnik (Kapitel 5), 2001, Vogel Buchverlag, ISBN 3-8023-1755-6
• Günter Wellenreuther, Dieter Zastrow: Steuerungstechnik mit SPS: Von der Steuerungsaufgabe zum Steuerprogramm (Kapitel 4.5.2), 1998, Vieweg+Teubner Verlag, ISBN 3-5284-4580-7

Weblinks

• Java-Applet zum KV-Diagramm von der Universität Karlsruhe
• Java-Applet zum KV-Diagramm von der Universität Erlangen-Nürnberg
• Kostenloses Lernprogramm. Lernziele: Aufstellen von Wahrheitstabellen und der disjunktiven Normalform (DNF), Vereinfachen von Schaltnetzen mit KV-Tafeln für 2 bis 5 Variable.
• Java-Applet zum KV-Diagramm mit Wertetabelle
• Herleitung einer Formel mittels KV-Diagramm zur Bestimmung, ob Rechtecke mit partiell gleichem Flächeninhalt überlappend angeordnet werden können, ein Artikel von Herbert Glarner [en]
• Applet zum bearbeiten von KV-Diagrammen der Universität Hamburg