- Vierter harmonischer Punkt
-
Dieser Artikel behandelt den mathematischen Begriff der harmonischen Teilung. In der Harmonielehre wird darunter meist die Teilung eines Intervalls entsprechend dem harmonischen Mittel verstanden. In der bildenden Kunst war „harmonische Teilung“ früher die Bezeichnung für den goldenen Schnitt und wird teilweise noch heute in diesem Sinne verwendet. - Ergibt sich nach dieser Formel ein negatives Ergebnis, so ist der Punkt U auf der Seite der Geraden einzutragen, die den Punkt B nicht enthält.
- Die Formel kann auch verwendet werden, wenn T der äußere und U der innere Teilpunkt ist. Liegt dann T von A aus gesehen auf der Seite der Geraden, die den Punkt B nicht enthält, so muss für
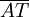eine negative Zahl eingetragen werden. 
.
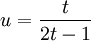Die harmonische Teilung bezeichnet in der Geometrie ein besonderes Lageverhältnis von vier Punkten auf einer Geraden. Eine harmonische Teilung liegt vor, wenn eine Strecke (zum Beispiel [AB]) durch zwei weitere Punkte (etwa T und U) innen und außen so geteilt wird, dass die beiden Teilverhältnisse (hier also (ABT) und (ABU)) den gleichen Betrag haben. Mit anderen Worten heißt das, dass das Doppelverhältnis (ABTU) = −1 ist.
Inhaltsverzeichnis |
Auffinden der Teilpunkte
Sind die Strecke [AB] und das Teilverhältnis λ gegeben, so lassen sich der innere und der äußere Teilpunkt nach den bei „Teilverhältnis“ angegebenen Methoden finden.
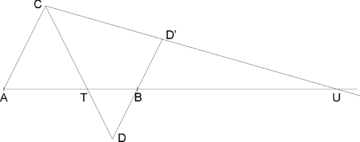
Oft sind jedoch eine Strecke und ein Teilpunkt gegeben, und zu finden ist der vierte harmonische Punkt (genauer: der 4. Punkt, der mit diesen 3 Punkten zusammen eine harmonische Teilung ergibt). Dazu hilft eine Konstruktion gemäß der nebenstehenden Zeichnung:
Der Punkt C wird beliebig gewählt, die Geraden AC und BD sind parallel. Punkt D (oder D') ergibt sich durch die Verbindung von C mit dem gegebenen Teilpunkt. D wird nach D' übertragen (oder umgekehrt), die Strecken [BD] und [BD'] sind gleich lang. Der fehlende Teilpunkt ergibt sich durch die Verbindung von C mit D' (oder D).
Rechnerisch ergibt sich die Länge der Strecke [AU], wenn die Länge von [AB] gegeben ist (und der Teilpunkt T), aus der Formel:
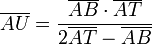
(Die Folgenden Punkte sind evtl. nicht mehr gültig, da o.g. Formel ueberarbeitet wurde, da jene nicht richtig war.)
Beziehungen und Sonderfälle
Wenn zwei Punkte T und U eine Strecke [AB] harmonisch teilen, so sind die Punkte A und B auch harmonische Teilpunkte der Strecke [TU]. Die harmonische Teilung ist also ein gegenseitiges Verhältnis von zwei auf der gleichen Gerade gelegenen Strecken.
Nicht ganz richtig ist es dagegen, zu sagen, dass „vier Punkte harmonisch zueinander liegen“. Nimmt man nämlich [AT] oder [AU] als Ausgangsstrecke, so erzeugen die beiden verbleibenden Punkte keine harmonische Teilung. Vielmehr sind die Doppelverhältnisse (ATBU) = 2 und (AUTB) = 1/2.
Der vierte harmonische Punkt zum Mittelpunkt einer Strecke ist der Fernpunkt der entsprechenden Geraden, und umgekehrt.
Der vierte harmonische Punkt zum Endpunkt einer Strecke ist dieser Punkt selbst.
Funktionszusammenhang
Für zwei gegebene Punkte A und B und einen dritten, veränderlichen Punkt T auf der Geraden AB ist die Zuordnung des zu T (bezüglich der Strecke [AB]) vierten harmonischen Punkts U eine umkehrbar eindeutige Abbildung der Geraden AB (einschließlich ihres Fernpunkts!) auf sich selbst.
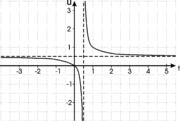
Verwendet man als Strecke [AB] das Intervall [0;1], und ist t die Koordinate des Punktes T, so ergibt sich die Koordinate u von U aus der Funktionsgleichung
Siehe auch
Weblinks
Wikimedia Foundation.
