- Viterbi
-
Der Viterbi-Algorithmus ist ein Algorithmus der Dynamischen Programmierung zur Bestimmung der wahrscheinlichsten Sequenz von versteckten Zuständen bei einem gegebenen Hidden Markov Model und einer beobachteten Sequenz von Symbolen. Diese Zustandssequenz wird auch als Viterbi-Pfad bezeichnet.
Er wurde von Andrew J. Viterbi (* 9. März 1935 in Bergamo, Italien, eigentlich Andrea Viterbi) 1967 zur Dekodierung von Faltungscodes entwickelt, er fiel quasi als Nebenprodukt bei der Analyse der Fehlerwahrscheinlichkeit von Faltungscodes ab. G. D. Forney leitete daraus 1972 den Optimalempfänger für verzerrte und gestörte Kanäle her. Der Viterbi-Algorithmus wird heutzutage zum Beispiel in Handys oder Wireless LANs zur Entzerrung oder Fehlerkorrektur der Funkübertragung verwendet. Ebenso in Festplatten, da bei der Aufzeichnung auf die Magnetplatten ebenfalls Verzerrungen entstehen.
Der Algorithmus ist in der Nachrichtentechnik und Informatik weit verbreitet: Die Informationstheorie, Spracherkennung, Bioinformatik und Computerlinguistik verwenden gerne den Viterbi-Algorithmus. Spracherkennung ohne diesen Algorithmus wäre schwer zu realisieren.
Inhaltsverzeichnis
Anwendungen
Der Viterbi-Algorithmus ist der optimale Algorithmus zur Dekodierung von Faltungscodes im Sinne der Blockfehlerrate (maximum likelihood sequence estimation). Der im Sinne der Symbolfehlerrate optimale Dekodieralgorithmus ist der BCJR-Algorithmus.
Wie man aus der Beschreibung des Algorithmus sieht, kann er fast überall eingesetzt werden, um Muster zu erkennen. Das ist ein weites Feld, da Lebewesen ständig Sinnesreize interpretieren müssen und aus dem bereits Gelernten diese Signale einordnen. Der Viterbi-Algorithmus tut genau das auch und ist somit ein wichtiger Baustein der Künstlichen Intelligenz.
Einen wichtigen Stellenwert nimmt der Algorithmus in der Bioinformatik ein, denn anhand des Viterbi-Algorithmus kann unter anderem von der tatsächlichen Sequenz eines DNA-Abschnitts auf eventuelle versteckte Zustände geschlossen werden. So kann zum Beispiel untersucht werden, ob es sich bei einer vorliegenden Sequenz wahrscheinlich um ein bestimmtes Strukturmotiv handelt (CpG-Insel, Promotor, ...) oder nicht. Vorteil dieses rekursiven Algorithmus ist hierbei der linear mit der Sequenzlänge steigende Aufwand im Gegensatz zum exponentiellen Aufwand des zugrundeliegenden Hidden Markov Model.
Algorithmus
Gegeben ist ein HMM M = (Σ,Q,A,E,π), wobei
- Σ das Alphabet der beobachtbaren Symbole bezeichnet
- Q die Menge der verborgenen Zustände bezeichnet
- A die Matrix der Zustandsübergangswahrscheinlichkeiten bezeichnet. Für
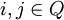 ist in der Zelle aij die Wahrscheinlichkeit für den Übergang von Zustand i nach j gespeichert.
ist in der Zelle aij die Wahrscheinlichkeit für den Übergang von Zustand i nach j gespeichert. - E die Matrix der Emissionswahrscheinlichkeiten bezeichnet. In der Zelle
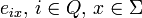 ist die Wahrscheinlichkeit gespeichert, dass im Zustand i das beobachtete Zeichen x ausgegeben wird.
ist die Wahrscheinlichkeit gespeichert, dass im Zustand i das beobachtete Zeichen x ausgegeben wird. - Der Vektor π, der für jeden Zustand die Wahrscheinlichkeit, dass in diesem Zustand gestartet wird, enthält.
u ist die gesuchte Sequenz von verborgenen Zuständen. Die Eingabe ist die beobachtete Sequenz von Symbolen m.
Initialisierung
![V[s, 1] = e_{s m[1]} \pi_s,\qquad s\in Q](/pictures/dewiki/56/8852a0bd5fab92788dfa267e9ba04dfc.png)
Rekursion
![V[s, i] = e_{s m[i]} \max_{t\in Q} a_{ts} V[t,i-1],\qquad s\in Q, 1<i\le |m|](/pictures/dewiki/53/5552f6ca7a3c777cd261910e277e43ea.png)
Terminierung
![P(u|m) = \max_{s\in Q} V[s, |m|]](/pictures/dewiki/48/08cdbb8e730c8c247c39a3dde1873656.png)
Pfadermittlung
Der Pfad u kann durch Backtracking in der Matrix V ermittelt werden. Z.B. kann während der Berechnung von V für jede Zelle vermerkt werden, welche Zellen an dem Maximum beteiligt sind. In einer Backtracking-Phase kann diese Information von
![argmax_{s\in Q} V[s, |m|]](/pictures/dewiki/99/cfc3703b1c17776810bdf784e0f22435.png) aus verfolgt werden.
aus verfolgt werden.Komplexität
Die Tabelle V benötigt O( | m | | Q | ) Speicher. Für jede Zelle wird über | Q | Alternativen optimiert. Also ist die Laufzeit in O( | m | | Q | 2).
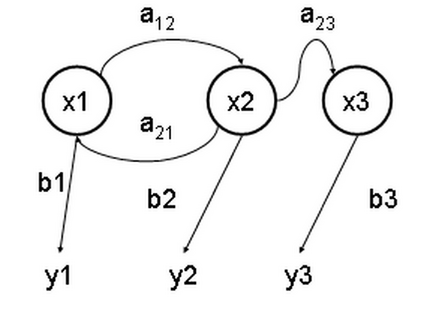
Veranschaulichung
Es bedeuten:
- x – (versteckte) Zustände des Markov-Modells
- a – Übergangswahrscheinlichkeiten
- b – Emissionswahrscheinlichkeiten
- y – (sichtbare) Ausgabesymbole
Siehe auch
Weblinks
- Patente aufbauend auf dem Viterbi-Algorithmus
- Erklärung des Viterbi-Algorithmus für Faltungscodes (englisch)
- Andrew J. Viterbi: „Viterbi algorithm“ in Scholarpedia (englisch, inkl. Literaturangaben)
Literatur
- A. Viterbi: Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. In: IEEE Transactions on Information Theory. 13, Nr. 2, 1967, ISSN 0018-9448, S. 260-269 (IEEE Xplore).
- Durbin et al.: Biological sequence analysis. Cambridge, 2006, ISBN 0-521-62971-3, S. 56.
- Forney Jr., G. D.: The Viterbi Algorithm.. In: In Proceedings of the IEEE. 61, Nr. 3, 1973, S. 268-278 (IEEE Xplore).
Wikimedia Foundation.