- Voller Funktor
-
Treue Funktoren und die hier ebenfalls zu besprechenden vollen und volltreuen Funktoren, die eng damit zusammenhängen, sind in der mathematischen Theorie der Kategorientheorie betrachtete Funktoren mit speziellen Eigenschaften.
Inhaltsverzeichnis
Definitionen
Sei
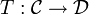 ein Funktor zwischen zwei Kategorien
ein Funktor zwischen zwei Kategorien 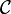 und
und 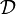 . Ein solcher Funktor ordnet definitionsgemäß jedem Objekt
. Ein solcher Funktor ordnet definitionsgemäß jedem Objekt 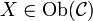 und jedem Morphismus
und jedem Morphismus 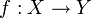 aus
aus 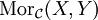 , wobei X und Y Objekte aus
, wobei X und Y Objekte aus 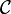 seien, ein Objekt
seien, ein Objekt 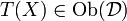 beziehungsweise einen Morphismus
beziehungsweise einen Morphismus 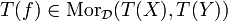 zu, wobei gewisse Verträglichkeitsbedingungen erfüllt sind (siehe Funktor).
zu, wobei gewisse Verträglichkeitsbedingungen erfüllt sind (siehe Funktor).Zu jedem Paar (X,Y) von Objekten aus
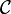 hat man eine Abbildung:
hat man eine Abbildung: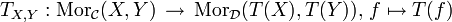
Man nennt den Funktor T treu (bzw. voll, bzw. volltreu), wenn die Abbildungen TX,Y für jedes Paar (X,Y) von Objekten aus
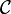 injektiv (bzw. surjektiv, bzw. bijektiv) sind. An Stelle von volltreu findet man auch die Bezeichnung völlig treu.
injektiv (bzw. surjektiv, bzw. bijektiv) sind. An Stelle von volltreu findet man auch die Bezeichnung völlig treu.Einbettungen
Ist
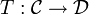 ein Funktor, so beziehen sich die Begriffe treu, voll und volltreu nur auf Morphismenmengen zwischen je zwei Objekten, sie beziehen sich nicht auf die Klassen aller Objekte bzw. aller Morphismen, insbesondere sagt die Treue des Funktors T nicht aus, dass eine der Abbildungen
ein Funktor, so beziehen sich die Begriffe treu, voll und volltreu nur auf Morphismenmengen zwischen je zwei Objekten, sie beziehen sich nicht auf die Klassen aller Objekte bzw. aller Morphismen, insbesondere sagt die Treue des Funktors T nicht aus, dass eine der Abbildungen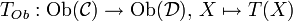
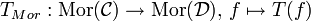
injektiv ist, was im Allgemeinen auch nicht der Fall ist. Um den Zusammenhang dieser Begriffe und die Verwendung obiger Definitionen zu beleuchten, wird hier die folgende einfache Aussage bewiesen:
- Wenn der Funktor T treu ist, so ist TOb genau dann injektiv, wenn TMor injektiv ist.
Ist TMor injektiv und sind
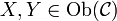 mit T(X) = T(Y), so folgt T(idX) = idT(X) = idT(Y) = T(idY), also nach Voraussetzung idX = idY und damit X = Y. Daher ist TOb injektiv. (Für diese Richtung wird die Treue des Funktors nicht benötigt.)
mit T(X) = T(Y), so folgt T(idX) = idT(X) = idT(Y) = T(idY), also nach Voraussetzung idX = idY und damit X = Y. Daher ist TOb injektiv. (Für diese Richtung wird die Treue des Funktors nicht benötigt.)Sei nun umgekehrt TOb injektiv, und seien
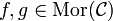 mit T(f) = T(g). Es gibt dann Objekte X1,X2,Y1,Y2 aus der Kategorie
mit T(f) = T(g). Es gibt dann Objekte X1,X2,Y1,Y2 aus der Kategorie 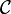 , so dass f und g Morphismen
, so dass f und g Morphismen 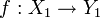 bzw.
bzw. 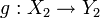 sind. Es ist f = g zu zeigen. Um die Treue des Funktors anwenden zu können, müssen wir X1 = X2 und Y1 = Y2 zeigen. Da T Funktor ist, erhält man Morphismen
sind. Es ist f = g zu zeigen. Um die Treue des Funktors anwenden zu können, müssen wir X1 = X2 und Y1 = Y2 zeigen. Da T Funktor ist, erhält man Morphismen 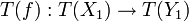 und
und 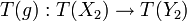 . Da T(f) = T(g), folgt T(X1) = T(X2) und T(Y1) = T(Y2). Weil TOb nach Voraussetzung injektiv ist, erhalten wir X1 = X2 und Y1 = Y2. Daher ist
. Da T(f) = T(g), folgt T(X1) = T(X2) und T(Y1) = T(Y2). Weil TOb nach Voraussetzung injektiv ist, erhalten wir X1 = X2 und Y1 = Y2. Daher ist 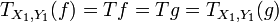 und die Treue von T liefert, wie gewünscht, f = g.
und die Treue von T liefert, wie gewünscht, f = g.Man nennt einen Funktor T eine Einbettung, wenn TMor injektiv ist. Für einen treuen Funktor ist die Einbettungseigenschaft nach Obigem äquivalent zur Injektivität von TOb.
Ist der Funktor
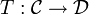 eine Einbettung, so bilden die Objekte
eine Einbettung, so bilden die Objekte 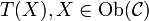 mit den Morphismen
mit den Morphismen 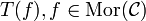 , eine Unterkategorie von
, eine Unterkategorie von 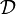 , die mit
, die mit 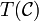 bezeichnet wird. Da das für beliebige Funktoren, die keine Einbettungen sind, im Allgemeinen nicht der Fall ist, spielen Einbettungen eine wichtige Rolle in der Kategorientheorie.
bezeichnet wird. Da das für beliebige Funktoren, die keine Einbettungen sind, im Allgemeinen nicht der Fall ist, spielen Einbettungen eine wichtige Rolle in der Kategorientheorie.Volltreue Funktoren
Ist der Funktor
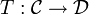 eine Einbettung, und ist T ein voller Funktor, so ist
eine Einbettung, und ist T ein voller Funktor, so ist 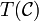 eine volle Unterkategorie von
eine volle Unterkategorie von 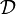 . Dies motiviert die Bezeichnung voller Funktor in obigen Definitionen. Ist also T ein volltreuer Funktor, so dass TOb injektiv ist, so definiert T eine Einbettung auf eine volle Unterkategorie.
. Dies motiviert die Bezeichnung voller Funktor in obigen Definitionen. Ist also T ein volltreuer Funktor, so dass TOb injektiv ist, so definiert T eine Einbettung auf eine volle Unterkategorie.Volltreue Funktoren sind auch wegen der folgenden Aussage wichtig für die Kategorientheorie:
- Seien
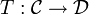 ein volltreuer Funktor und
ein volltreuer Funktor und 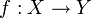 ein Morphismus der Kategorie
ein Morphismus der Kategorie 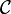 . Dann gilt: f ist Isomorphismus
. Dann gilt: f ist Isomorphismus 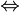 Tf ist Isomorphismus.
Tf ist Isomorphismus.
Die Richtung von links nach rechts ist sehr einfach. Ist nämlich f Isomorphismus, so gibt es definitionsgemäß einen weiteren Morphismus
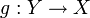 mit fg = idY und gf = idX. Da T Funktor ist, folgt
mit fg = idY und gf = idX. Da T Funktor ist, folgt 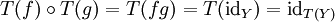 und genauso
und genauso 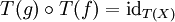 , das heißt, T(f) ist ein Isomorphismus.
, das heißt, T(f) ist ein Isomorphismus.Die Volltreue wird für die Umkehrung benötigt. Ist nämlich
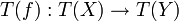 ein Isomorphismus, so gibt es einen Morphismus
ein Isomorphismus, so gibt es einen Morphismus 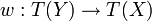 mit
mit 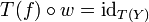 und
und 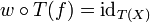 . Da T voll ist, gibt es einen Morphismus
. Da T voll ist, gibt es einen Morphismus 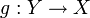 mit T(g) = w. Dann folgt
mit T(g) = w. Dann folgt 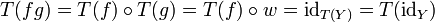 und genauso
und genauso 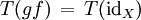 . Wegen der Treue von T folgt nun fg = idY und gf = idX, das heißt, f ist ein Isomorphismus.
. Wegen der Treue von T folgt nun fg = idY und gf = idX, das heißt, f ist ein Isomorphismus.Literatur
- Horst Schubert: Kategorien I/II. Springer-Verlag, 1970.
Wikimedia Foundation.
