Von-Neumann-Morgenstern-Erwartungsnutzen

Dieser Artikel oder Abschnitt ist nicht hinreichend mit Belegen (Literatur, Webseiten oder Einzelnachweisen) versehen. Die fraglichen Angaben werden daher möglicherweise demnächst gelöscht. Hilf Wikipedia, indem du die Angaben recherchierst und gute Belege einfügst. Bitte entferne erst danach diese Warnmarkierung.

Nutzenfunktion U(x)

Die Nutzenfunktion ist in der Volkswirtschaftslehre eine häufig gewählte Modellierung der Präferenzen einzelner Wirtschaftssubjekte. Grundlegende Annahme des Konzepts ist, dass der Akteur als homo oeconomicus gesehen wird, der danach strebt, aus der Menge ihm zur Verfügung stehender Alternativen diejenige mit dem größten Nutzen auszuwählen. Werden Präferenzen durch Nutzenfunktionen repräsentiert, so bedeutet dies, dass ein Individuum jene Entscheidungen trifft, für die es – gegeben die Restriktionen, denen sein Handeln unterliegt – den größtmöglichen Nutzen erwartet.

Das Konzept der Nutzentheorie wird dabei sowohl in der Mikroökonomie als auch in der Makroökonomie eingesetzt. Geht es in der Mikroökonomie darum, das Verhalten einzelner Wirtschaftssubjekte zu erklären, werden in der Makroökonomie die Präferenzen wirtschaftspolitischer Entscheidungsträger mit Hilfe von Nutzenfunktionen dargestellt.

Nutzentheorie in der Mikroökonomie

In der mikroökonomischen Theorie geht man davon aus, dass Individuen Präferenzen über die ihnen potenziell zur Verfügung stehenden Auswahlalternativen (z. B. Konsumgüterbündel) haben. Mathematisch lassen sich derartige Präferenzen (die sehr allgemein sein können) als binäre Relationen darstellen. Diese Relation ordnet je zwei Alternativen A und B die Aussagen „A wird vom Individuum mindestens so hoch geschätzt wie B“, „B wird vom Individuum mindestens so hoch geschätzt wie A“, oder „A und B sind aus Sicht des Individuums nicht vergleichbar“.

Eine häufig getroffene Annahme ist, dass Präferenzen totale Ordnungen sind, d. h. dass die ihnen zugrunde liegenden binären Relationen vollständig (es gibt keine Nichtvergleichbarkeiten von Alternativen), reflexiv (jede Alternative wird mindestens so hoch geschätzt wie sie selbst) und transitiv sind (Wenn A vom Individuum mindestens so hoch geschätzt wird wie B und B mindestens so hoch geschätzt wird wie C, dann wird A auch mindestens so hoch geschätzt wie C).

Existiert eine Präferenzordnung über einer Alternativenmenge, so lässt sie sich durch eine reellwertige Funktion mit folgender Interpretation darstellen: Eine Alternative A wird genau dann mindestens so gut eingeschätzt wie eine Alternative B, wenn der Wert der Funktion für A nicht kleiner ist als der Wert der Funktion für B. Diese Funktion heißt dann Nutzenfunktion. Sie ist eine bequeme mathematische Abbildung individueller Präferenzen.

Von besonderer analytischer Bedeutung ist für eine (beliebige) Alternative A die Menge aller Alternativen, die mindestens so gut eingeschätzt werden wie A. Diese Menge heißt Bessermenge von A. Ihr Rand, d. h. die Menge aller Alternativen, die von einem Individuum als gleichwertig zu A eingeschätzt werden, heißt Indifferenzmenge zu A. Bei Repräsentation der Präferenzen durch eine Nutzenfunktion stiften alle Elemente der Indifferenzmenge zu A denselben Nutzen wie A. Graphisch wird die Indifferenzmenge zu einer Alternative als Indifferenzkurve dargestellt; inhaltlich kann man auch von einer Indifferenzkurve zu einem bestimmten Nutzenniveau (statt zu einer Alternative) sprechen.

In der mikroökonomischen Theorie der Konsumgüternachfrage (Haushaltstheorie) bezeichnet man die Werte der Nutzenfunktion als das Nutzenniveau, das ein individueller Konsument durch den Konsum bestimmter Güterbündel erreicht:

$u=U(C_1,C_2,\ldots,C_n)$.

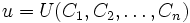Dabei bezeichnen U die Nutzenfunktion, u das Nutzenniveau und 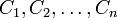$C_1,C_2,\ldots,C_n$ die Güterbündel. Da der Raum der Güterbündel oft durch die n-dimensionalen reellen Zahlen modelliert wird, unterstellt man oft, dass U stetig differenzierbar ist.

Eine Indifferenzkurve zum Nutzenniveau 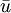$\bar u$ ist die Menge aller Konsumgüterbündel 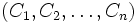$(C_1,C_2,\ldots,C_n)$, für die gilt: $U(C_1,C_2,\ldots,C_n)=\bar u$.

Durch Optimierung über die Nutzenfunktion versucht der Konsument, sein Haushaltsoptimum zu erlangen.

Grenznutzen

Die erste Ableitung 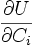$\frac{\partial U}{\partial C_i}$ der Nutzenfunktion nach einem Güterbündel C_i bezeichnet man als Grenznutzen dieses Gutes. Anschaulich gibt der Grenznutzen an, wie viel zusätzlichen Nutzen eine weitere Einheit des Gutes C_i stiften würde.

Ein Grenznutzen von 0 bedeutet, dass für dieses Gut Sättigung eingetreten ist. Eine weitere Einheit dieses Gutes würde keinen zusätzlichen Nutzen stiften.

Allgemeine Annahmen

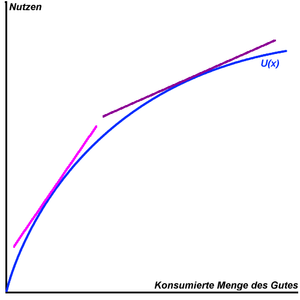
Bei normalen Gütern geht man oft davon aus, dass zusätzlicher Konsum grundsätzlich einen höheren Nutzen stiftet, selbst wenn die bereits konsumierte Menge sehr groß ist. Das heißt, dass die Nutzenfunktion in jedem ihrer Argumente streng monoton steigt beziehungsweise dass der Grenznutzen auch für große C_i positiv ist.

In der traditionellen Nutzentheorie unterstellt man häufig, dass der Nutzengewinn durch den Konsum einer zusätzlichen Einheit eines Gutes mit der Höhe der bereits konsumierten Menge diesen Gutes abnimmt, wie dies bereits im ersten Gossenschen Gesetz festgestellt wird. Man spricht dabei von abnehmendem Grenznutzen beziehungsweise konkaver Nutzenfunktion. Diese Annahme ist im Allgemeinen unnötig. Benötigt wird als Annahme gemeinhin nur die Quasi-Konkavität der Nutzenfunktion (abnehmende Grenzrate der Substitution zwischen je zwei Gütern; konvexe Bessermengen bzw. Indifferenzkurven).

Quasilineare Nutzenfunktionen

Eine Nutzenfunktion ist quasilinear, wenn sie die Form U(C₁,C₂) = v(C₁) + C₂ besitzt. Die Indifferenzkurven von quasilinearen Nutzenfunktionen unterscheiden sich nur durch die Höhe des vertikalen Achsenabschnitts. Bei einer gegebenen Menge des Gutes C₁ haben somit alle Indifferenzkurven die gleiche Steigung. Zudem ist die Grenzrate der Substitution zwischen C₁ und C₂ unabhängig von C₂.

Quasilineare Nutzenfunktionen spielen eine bedeutende Rolle in der Mechanismus-Design-Theorie und der Auktionstheorie.

Indirekte Nutzenfunktion

Die indirekte Nutzenfunktion (V) gibt das Nutzenniveau an, das ein Konsument bei einer bestimmten Einkommenshöhe und bei bestimmten Konsumgüterpreisen maximal erreichen kann:

$V(M,P_1,P_2,\ldots,P_n) = \max \{U(C_1, \ldots, C_n) | \sum P_i C_i \leq M \}$.

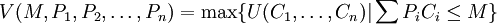Dabei bezeichnet M das Einkommen des Konsumenten und P_i den Preis des Konsumgutes i. Der indirekten Nutzenfunktion liegt (hier im Zusammenhang mit der Konsumgüternachfrage) die Idee zugrunde, dass Individuen nutzenmaximierend agieren, d. h., aus den ihnen zur Verfügung stehenden Alternativen (hier begrenzt durch das Einkommen) die ihnen am besten erscheinende auswählen.

Intertemporale Nutzenfunktion

Eine intertemporale Nutzenfunktion bildet Präferenzen über Konsumalternativen ab, die zu verschiedenen Zeitpunkten zur Verfügung stehen. Mit ihr kann u. a. erklärt werden, warum und in welcher Höhe Menschen sparen oder Kredite aufnehmen.

In Einklang mit empirisch beobachtbarem Verhalten geht man bei intertemporalen Präferenzen oft davon aus, dass Individuen einen zeitnäheren Konsum gegenüber einem zeitfernerer Konsum in gleicher Höhe vorziehen; man spricht hier von einer positiven Zeitpräferenz. In Nutzenfunktionen wird diese positive Zeitpräferenz häufig durch Diskontfaktoren abgebildet, wobei man vereinfachend oft von einer konstanten Zeitpräferenzrate auch bei Einkommensveränderungen ausgeht. Vermutlich hat der Gegenwartskonsum aber bei niedrigeren Einkommen einen höheren Nutzen, und bei einen Pro-Kopf-Einkommen an der Armutsgrenze ist die Zeitpräferenzrate entsprechend sehr hoch.

Die Zeitpräferenzrate eines Wirtschaftssubjektes ist die private Zeitpräferenzrate, während die einer Gesellschaft als soziale Zeitpräferenzrate bezeichnet wird.

Die Konzepte der Bessermenge oder der Indifferenzkurve lassen sich analog anwenden.

Erwartungsnutzenfunktion

Bei Entscheidungen unter Unsicherheit wird der Nutzen einer sog. Lotterie oft mittels Erwartungsnutzenfunktion modelliert, die den Nutzen von riskanten Alternativen (also der Lotterie) wiedergibt.

Dabei wird der Erwartungswert über eine (typischerweise eindimensionale) Nutzenfunktion für die einzelnen Alternativen als Nutzenwert definiert. Die Nutzenfunktion der jeweiligen Alternativen und deren Wahrscheinlichkeitsverteilung bestimmen daher den Nutzen einer Lotterie: Erwartungsnutzen ist einfach der Erwartungswert des Nutzens der Alternativen. Eine solche Nutzenfunktion wird auch als Von-Neumann-Morgenstern-(Erwartungs)-Nutzenfunktion bezeichnet.

$V(z)=E[u(z)]=\sum_{i=1}^N p_i\cdot u(z_i)$

V bezeichnet die Erwartungsnutzenfunktion über die Zufallsvariable z (i Zustände, die mit unterschiedlichen Wahrscheinlichkeiten p eintreten) und u ist die sogenannte Bernoulli-Nutzenfunktion in Abhängigkeit von z. Die Von-Neumann-Morgenstern-Nutzenfunktion ist somit nichts anderes als der mit den Wahrscheinlichkeiten gewichtete Nutzen aus den verschiedenen Zuständen, die aus der Lotterie resultieren könne.

Die Existenz einer Erwartungsnutzenfunktion setzt jedoch stärkere Annahmen voraus, insbesondere das umstrittene Unabhängigkeitsaxiom, gemäß dem irrelevante Alternativen keinen Einfluss auf das Ergebnis haben dürfen. Unabhängig von der Zulässigkeit einer Erwartungsnutzenformulierung können ökonomisch Handelnde als risikoneutral, risikofreudig oder risikoavers eingestuft werden.

Häufig verwendete Nutzenfunktionen

• exponentielle Nutzenfunktion
• homothetische Nutzenfunktion
• Cobb-Douglas-Nutzenfunktion

Recoverability-Problem

Als Recoverability-Problem bezeichnet man die Fragestellung aus einer Nutzenfunktion die Präferenzordnung zu bestimmen, die die vorgelegte Nutzenfunktion erzeugt. Dies ist die Umkehrung des Problems, zu einer Präferenzordnung eine Nutzenfunktion mit bestimmten Merkmalen zu finden.

Makroökonomische Nutzentheorie

Im makroökonomischen Zusammenhang finden gesamtwirtschaftliche Nutzenfunktionen Verwendung, um die Vorteilhaftigkeit bestimmter politischer und ökonomischer Entwicklungen für die gesamtwirtschaftliche Entwicklung zu messen.

In der Makroökonomie wird das Konzept ebenfalls genutzt, um die Verhaltensweise wirtschaftspolitischer Akteure zu modellieren. In diesem Kontext werden im Rahmen der Public-Choice-Theorie beispielsweise Nutzenfunktionen für wiederwahlorientierte Politiker erstellt. Demnach werden Politiker diejenige politische Alternative wählen, die ihren Wiederwahlchancen am meisten nützt.