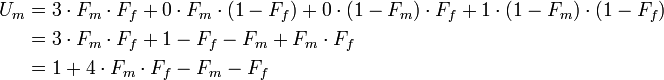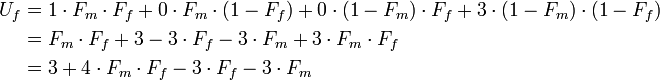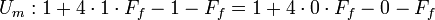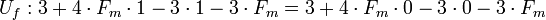Battle of Sexes

Der Kampf der Geschlechter ist ein Problem aus der Spieltheorie. Zwei Spieler wollen gemeinsam den Abend verbringen, vergessen aber, sich über den Ort zu einigen. Möglich ist entweder ein Fußballspiel oder ein Konzert. Beide Spieler müssen sich unabhängig voneinander entscheiden. Das Fußballspiel wird von dem Mann, das Konzert von der Frau präferiert.

Die Auszahlungs-Matrix für das Spiel sieht bei symmetrischer Betrachtungsweise folgendermaßen aus:

Mann\Frau	Fußball	Konzert
Fußball	(3, 1)	(0, 0)
Konzert	(0, 0)	(1, 3)

Erklärung zur Matrix: „Auszahlung“ des Mannes steht an erster Stelle, die der Frau an zweiter. Geht die Frau also ins Fußballstadion, wäre die beste Wahl des Mannes, auch dorthin zu gehen. Umgekehrt gilt das gleiche, daher ist die linke obere Zelle ein Nash-Gleichgewicht. Analog verhält es sich mit der Konzerthalle. Es gibt also zwei Nash-Gleichgewichte in reinen Strategien.

Das Problem dieses Spiels ist nun, dass es keine dominanten Strategien gibt. Wenn die beiden Spieler gleichzeitig ihre Lieblingsalternative (Frau geht ins Konzert, Mann zum Fußball.) wählen, kommt es zu keinem Treffen, was für beide nicht optimal ist. Sie würden in diesem Fall doch lieber an den Ort gehen, den der jeweils andere bevorzugt – Hauptsache, sie sind zusammen. Wenn aber beide so denken und dem anderen entgegen kommen möchten, treffen sie sich wieder nicht.

Als Ausweg könnten die Spieler per Zufall entscheiden (randomisieren), welchen Ort sie heute Abend aufsuchen werden. Dafür gibt es ein Gleichgewicht in gemischten Strategien.

Wir stellen eine Von-Neumann-Morgenstern-Nutzenfunktion auf:

U_f = Nutzen der Frau

U_m = Nutzen des Mannes

F_f = Wahrscheinlichkeit, dass die Frau zum Fußball geht.

F_m = Wahrscheinlichkeit, dass der Mann zum Fußball geht.

$\begin{align} U_m &= 3 \cdot F_m \cdot F_f + 0 \cdot F_m \cdot (1 - F_f) + 0 \cdot (1 - F_m) \cdot F_f + 1 \cdot (1-F_m) \cdot (1-F_f) \\ &= 3 \cdot F_m \cdot F_f + 1 - F_f - F_m + F_m \cdot F_f \\ &= 1 + 4 \cdot F_m \cdot F_f - F_m - F_f \end{align}$

$\begin{align} U_f &= 1 \cdot F_m \cdot F_f + 0 \cdot F_m \cdot (1-F_f) + 0 \cdot (1-F_m) \cdot F_f + 3 \cdot (1-F_m) \cdot (1-F_f) \\ &= F_m \cdot F_f + 3 - 3 \cdot F_f - 3 \cdot F_m + 3 \cdot F_m \cdot F_f \\ &= 3 + 4 \cdot F_m \cdot F_f - 3 \cdot F_f - 3 \cdot F_m \end{align}$

Wenn ein Spieler die dem Nashgleichgewicht in gemischten Strategien entsprechende randomisierte Strategie spielt, ist der andere Spieler indifferent zwischen den reinen Strategien, die er in diesem Nashgleichgewicht mit positiver Wahrscheinlichkeit spielt, d. h. jede dieser reinen Strategien bringt ihm den gleichen Erwartungsnutzen. Das lässt sich ausnutzen, um das Nashgleichgewicht zu berechnen. Es muss dann nämlich gelten:

$U_m: 1 + 4 \cdot 1 \cdot F_f - 1 - F_f = 1 + 4 \cdot 0 \cdot F_f - 0 - F_f$

$U_f: 3 + 4 \cdot F_m \cdot 1 - 3 \cdot 1 - 3 \cdot F_m = 3 + 4 \cdot F_m \cdot 0 - 3 \cdot 0 - 3 \cdot F_m$

Aus der ersten Gleichung folgt F_f = 0,25 und aus der zweiten F_m = 0,75.

Daraus folgt, dass beide in 25% aller Fälle den Lieblingsort ihres Partners aufsuchen sollten.

"Battle of the sexes" wird in der Regel für den Einstieg in die gemischten Strategien gewählt, weil es noch recht einfach zu errechnen ist. Interessant werden die Prozentangaben für gemischte Strategien z. B. beim Tennis oder beim Elfmeterschießen (siehe Dixit/Nalebuff), wo es ebenfalls keine dominanten Strategien gibt, die Wiederholungsrate aber entsprechend hoch ist.

Bei nichtsymmetrischer Bewertung entstehen andere, wenn auch prinzipiell ähnliche Ergebnisse.

Bimatrix (Kampf der Geschlechter)

Siehe auch

• Gefangenendilemma
• Spiel mit dem Untergang (chicken game)
• Hirschjagd
• Braess-Paradoxon