W*-Algebra

Eine von-Neumann-Algebra oder W*-Algebra ist eine mathematische Struktur in der Funktionalanalysis.

Definition

Eine von-Neumann-Algebra (benannt nach John von Neumann) oder (mittlerweile veraltet) ein Ring von Operatoren ist eine *-Unteralgebra mit Eins der Algebra 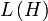$L\left(H\right)$ der beschränkten linearen Operatoren eines Hilbertraums H, die eine (und damit alle) der drei folgenden äquivalenten Bedingungen erfüllt:

• A = A''.
• A ist abgeschlossen in der starken Operatortopologie.
• A ist abgeschlossen in der schwachen Operatortopologie.

Hierbei ist 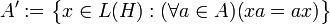$A' := \bigl\{ x \in L(H) : (\forall a \in A)(xa = ax)\bigr\}$ die Kommutante von A.

Die Äquivalenz der drei obigen Aussagen nennt man den von Neumannschen Doppelkommutantensatz oder Bikommutantensatz. Diese Aussage kann wie folgt verschärft werden:

• Ist 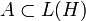$A\subset L(H)$ eine *-Unteralgebra mit Eins, so ist A'' der Abschluss von A sowohl in der schwachen als auch in der starken Operatortopologie.

Auch diese Formulierung, die eine Äquivalenz zwischen der rein algebraischen Kommutanten-Bildung und der rein topologischen Dichte-Beziehung bzw. Abschluss-Bildung herstellt, wird als Bikommutantensatz bezeichnet. Damit erweist sich der Bikommutantensatz als ein Dichtheitssatz. Zusammen mit dem weiteren Dichtheitssatz von Kaplansky stellt er den Ausgangspunkt der Theorie der von-Neumann-Algebren dar.

Eine Von-Neumann-Algebra kann nach einem Satz von Shôichirô Sakai auch abstrakt ohne einen zugrundeliegenden Hilbertraum definiert werden:

• Eine Von-Neumann-Algebra A ist eine C*-Algebra, die der topologische Dualraum eines Banachraums $A_{\star}$ ist.

Faktoren

Die von-Neumann-Algebra A heißt Faktor, falls sie eine der beiden folgenden äquivalenten Bedingungen erfüllt:

• $A \cap A' = \mathbb C 1$.
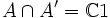• A und A' erzeugen $L\left(H\right)$.

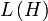Da 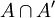$A \cap A'$ die Menge der Operatoren aus A ist, die mit allen Operatoren aus A kommutieren, ist 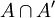$A \cap A'$ das Zentrum von A. Faktoren sind daher die von-Neumann-Algebren mit kleinst möglichem Zentrum. Man kann von-Neumann-Algebren als direktes Integral (eine Verallgemeinerung der direkten Summe) von Faktoren darstellen, das heißt von-Neumann-Algebren sind in diesem Sinne aus Faktoren zusammengesetzt.

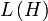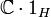$L\left(H\right)$ und $\C\cdot 1_H$ sind Beispiele für Faktoren. Mit A ist auch A' ein Faktor; offenbar gilt 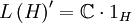$L\left(H\right)'=\C\cdot 1_H$ und $(\C\cdot 1_H)' = L\left(H\right)$.

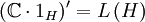Kommutative von-Neumann-Algebren

Sei 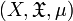$(X,{\mathfrak X},\mu)$ ein σ-endlicher Maßraum. Dann ist H = L²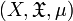$(X,{\mathfrak X},\mu)$ ein Hilbertraum, und jede wesentlich beschränkte Funktion 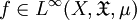$f\in L^{\infty}(X,{\mathfrak X},\mu)$ definiert via Multiplikation einen Operator 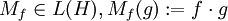$M_f\in L(H), M_f(g):=f\cdot g$. Die Abbildung 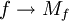$f\to M_f$ ist ein *-Isomorphismus von 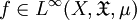$f\in L^{\infty}(X,{\mathfrak X},\mu)$ auf eine kommutative von-Neumann-Algebra 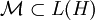${\mathcal M}\subset L(H)$, man kann sogar 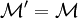${\mathcal M}' = {\mathcal M}$ zeigen, das heißt die Algebra 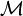${\mathcal M}$ stimmt mit ihrem Kommutanten überein. Keine echte Oberalgebra kann daher kommutativ sein, 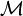${\mathcal M}$ ist also eine maximale kommutative von-Neumann-Algebra.

Betrachtet man speziell den Maßraum $([0,1],{\mathcal B},\lambda)$ (Einheitsintervall mit dem Lebesgue-Maß), so kann man zeigen, dass der Bikommutant von $\{M_f;\, f\in C([0,1])\}$ mit ${\mathcal M}\cong L^{\infty}([0,1])$ zusammenfällt. Der Übergang vom topologischen Konstrukt C([0,1]) zum maßtheoretischen Konstrukt $L^{\infty}([0,1])$ entspricht dem Übergang von C*-Algebren zu von-Neumann-Algebren. Während man bei C*-Algebren wegen des Satzes von Gelfand-Neumark von nicht-kommutativer Topologie spricht, gibt die hier angestellte Betrachtung Anlass, eine von-Neumann-Algebra als einen nicht-kommutativen Maßraum anzusehen, man spricht daher auch von nicht-kommutativer Maßtheorie.

Eigenschaften

Jede von-Neumann-Algebra ist eine C*-Algebra und somit auch eine Banachalgebra.

Wie sich aus dem beschränkten Borel-Funktionalkalkül ergibt, enthalten von-Neumann-Algebren sehr viele Orthogonalprojektionen; jeder Operator ist in der Normtopologie Limes von Linearkombinationen von Orthogonalprojektionen. Dies ist ein wesentlicher Unterschied zu den C*-Algebren, die, wie das Beispiel C([01]) zeigt, neben 0 und 1 keine weiteren Projektionen enthalten müssen. Man kann aus der Menge der Projektionen einen Verband konstruieren; die Struktur dieses Verbandes wird zur Typklassifikation der von-Neumann-Algebren herangezogen.

Literatur

• Jacques Dixmier: Von Neumann algebras. North-Holland, Amsterdam 1981, ISBN 0-444-86308-7
• Shôichirô Sakai: C*-Algebras and W*-Algebras, 1971 Springer-Verlag, ISBN 3540636331
• Jacob T. Schwartz: W-*Algebras, ISBN 0-677-00670-5